8.1. Доказать, что эта кривая - гипербола.

8.2. Найти координаты ее центра симметрии.

8.3. Найти действительную и мнимую полуоси.

8.4. Записать уравнение фокальной оси.

8.5. Построить данную гиперболу.

Решение.

8.1. Известно, что каноническое уравнение гиперболы имеет вид: -= 1. Преобразуем уравнение (8.1), выделив полные квадраты: 4(х - 4)²- (у - 3)²= 4, или-= 1. Положим х₁= (х - 4), у₁= (у - 3), тогда-= 1. Данное уравнение определяет гиперболу.

8.2. Решая систему уравнений х₁= 0 и у₁= 0, находим центр симметрии - точку О₁с координатами (4;3).

8.3. Из канонического уравнения гиперболы, найденного в п.8.1., видно, что действительная полуось а = = 1, мнимая -b== 2.

8.4. В новой системе координат оси направлены по прямым х - 4 = 0 (ось ОY₁) и у - 3 = 0 (ось ОХ₁), которая и является фокальной осью.

8.5. Для построения более точного графика найдем асимптоты данной гиперболы и точки ее пересечения со старыми осями координат. Известно, что асимптотами гиперболы являются прямые y= x. Из этого соотношения находим уравнения асимптот:

Кривая пересекает ось ОХ в точках (2,2;0) и (5,8;0), ось ОY- в точках (0;-4,7) и (0;10,7). Строим данную гиперболу.

Y₁

Y

10,7

3 y = 3

O₁X₁

O2,245,8 X

-4,6

9. Дана кривая 4x + 6y - y² = 21. (9.1)

9.1. Доказать, что данная кривая - парабола.

9.2. Найти координаты ее вершины.

9.3. Найти значение ее параметра p.

9.4. Записать уравнение ее оси симметрии.

9.5. Построить данную параболу.

Решение.

9.1. Каноническое уравнение параболы имеет вид: у² = 2рх. Преобразуем уравнение (9.1), выделив полные квадраты: (у - 3)²= 4(х - 3). Положим у₁= у - 3, х₁= х - 3, тогда уравнение приводится к виду= 4х₁. Данное уравнение определяет параболу.

9.2. Решая систему уравнений у₁= 0 и х₁= 0, находим вершину параболы - точку О₁с координатами (3;3).

9.3. Из канонического уравнения параболы, найденного в п.9.1., видно что 2р = 4, р = 2.

9.4. В новой системе координат оси направлены по прямым х - 3 = 0 (ось ОY₁) и у - 3 = 0 (ось ОХ₁), которая и является осью симметрии данной параболы.

9.5. Для построения более точного графика найдем точки пересечения данной кривой со старыми осями координат. Кривая пересекает только ось ОХ в точке (5,25;0). Строим кривую.

Y₁

Y

3 y= 3

O₁X₁

O35,25X

10. Дана кривая 5x² + 5y² + 8xy - 18x - 18y + 9 = 0.(10.1)

10.1. Доказать, что эта кривая - эллипс.

10.2. Найти координаты его центра симметрии.

10.3. Найти большую и малую полуоси.

10.4. Записать уравнение фокальной оси.

10.5. Построить данную кривую.

Решение.

10.1. Квадратичную форму В (х,у) = 5х²+ 5у²+ 8ху приводим к главным осям. Для этого записываем матрицу этой формы В =и находим ее собственные числа и собственные векторы. Составим и решим характеристическое уравнение этой матрицы:

= 0, (5 - λ)²- 16 = 0.

Его корни λ₁= 1, λ₂= 9 являются собственными числами. Т.к. λ₁· λ₂ > 0, то кривая (10.1) - эллипс.

10.2. Координаты собственного вектора, отвечающего числу λ₁= 1, удовлетворяют соотношению ξ₁= -ξ₂. В качестве нового базисного вектора примем векторi₁= ;-. Другой базисный векторj₁=;. Записываем матрицуQперехода от базисаO,i,jк базисуO,i₁,j₁:

Q = , Q^-1 = Q^T = .

По формуле перехода от одного базиса к другому выражаем старые координаты х и у через новые х₁и у₁:

=Q ,= , отсюдаx= ,y= .

Уравнение (10.1) в новой системе координат примет вид:

-= -9, или (10.2)

Произведем параллельный перенос системы координат в новое начало О₁по формулам:

x₂ = x₁, y₂ = y₁ -

х₁и у₁найдем по формулам:

= Q^-1 , = .

x₁ = , y₁ = ;

x₂= ,y₂= .

Решая систему уравнений х₂= 0 и у₂= 0, найдем координаты нового начала О₁(1;1). Точка О₁(1;1) - центр симметрии эллипса.

10.3. Уравнение (10.2) приводим к каноническому уравнению эллипса: += 1. Отсюда большая полуось а == 3, малаяb== 1.

10.4. В новой системе коорндинат оси направлены по прямым у = х (ось О₁Y₂) и у = - х + 2 (осьO₁X₂), которая и является фокальной осью эллипса.

10.5. Для построения более точного графика найдем дополнительные точки кривой эллипса. Например, точки пересечения со старыми осями координат. Ось OYкривая пересекает в точках (0;0,6) и (0;3); осьOX- в точках (0,6;0) и (3;0). Строим данную кривую.

Y

Y₂

O

X

X₂

Задание №1

Даны координаты вершин треугольника А(3,4), В(-1,2), С(2,-1). Записать общее уравнение средней линии треугольника, параллельной ВС.

Решение: точка М – точка середины отрезка АВ и точка К – середина отрезка АС. Тогда Следовательно, уравнение средней линии можно записать:

Ответ: х+у-4=0.

Задание №2

В прямоугольном треугольнике АВС известны: уравнение медианы 3х-4у+8=0, проведенной из вершины А(0,2) прямого угла, и вершина В(2,1). Найти координаты вершины С.

Решение: Точка М середина отрезка ВС, тогда

Ответ: С(2,6).

Задание №3

Записать общее уравнение плоскости, проходящей через точки М₁(7,2,-3) и М₂(5,6,-4) параллельно оси ОУ.

Решение:

Ответ: х-2z-13=0.

Задание №4

Найти коэффициент В в уравнении плоскости Ах+Ву+Сz +D=0, проходящей через точки

Р(1,-1,1), О(0,0,0) параллельно прямой

Решение: или

Ответ: В=4.

Задание №5

При каких значениях параметров А₁ и А₂ прямая параллельно прямой

Решение: Зададим данные прямые параметрически

Так как прямые параллельны, тогда имеет место

Ответ: А₁=1, А₂+2.

Задание№6

Найти длину отрезка, отсекаемого от оси аппликат, плоскостью, содержащей прямую и отсекающей на осях абсцисс и ординат одинаковой длины отрезки.

Решение: Зададим уравнение плоскости 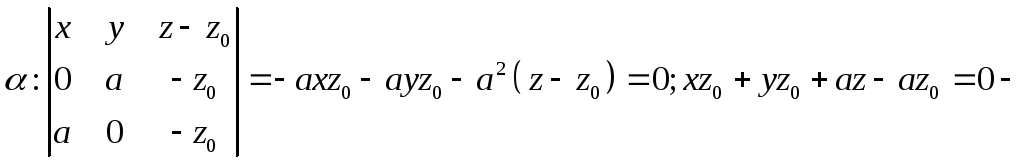уравнение заданной плоскости. Так как прямая а лежит в плоскости α, тогда и точки М₁ и М₂ прямой лежат в плоскости α. Имеем

Ответ: 5.

Задание №7

Найти уравнение касательной плоскости к сфере в точке М₀(1,1,2).

Решение:

Центр сферы в точке С(4,-3,-2). и радиусом равным . Вектор СМ₀ =(-3,4,4) является вектором нормали касательной плоскости к сфере в точке М₀(1,1,2).. Поэтому уравнение этой плоскости будет иметь вид

Ответ:

Задание №8

Дана кривая

1. Доказать, что эта кривая – гипербола.

2. Найти её координаты центра симметрии.

3. Найти действительную и мнимую полуоси.

4. Записать уравнение фокальной оси.

5. Построить данную гиперболу.

Решение:

b=2 – мнимая полуось, а=1 – действительная полуось, (4,3) – центр симметрии, уравнение фокальной оси у=3

Задание №9

. Дана кривая

• Доказать, что эта кривая – парабола.

• Найти её координаты вершины.

• Найти значение её параметра р.

• Записать уравнение её оси симметрии.

• Построить данную параболу.

Решение:

Мы получили уравнение параболы с вершиной в точке А(3,3), р.=2, уравнение оси симметрии у=3.

Задание №10

Дана кривая

• Доказать, что эта кривая – эллипс.

• Найти её координаты центра симметрии.

• Найти большую и малую полуоси.

• Записать уравнение фокальной оси.

• Построить данную кривую.

а=1, b=3 – большая и малая полуоси. Найдем центр симметрии эллипса координаты центра симметрии эллипса.

х+у=2, у=2-х –ось О₁У₂, у-ч=0, у=х – ось О₁Х₂.