Министерство образования

Российской Федерации

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра промышленной электроники (ПрЭ)

Контрольная работа №2 по дисциплине

Высшая Математика 1

Студент

Руководитель

________________

Вариант № 1.

Задание 1.

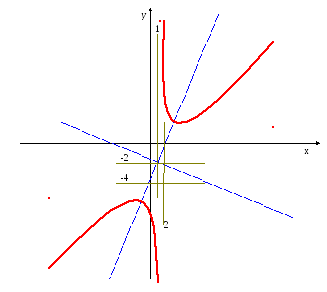
Записать уравнение прямой, проходящей через точки М₁(-1,2) и

М₂(-3,-2). Найти значения параметров k и b для этой прямой.

Уравнение имеет вид: y=kx+b. Подставим в уравнение значение точек и получим:

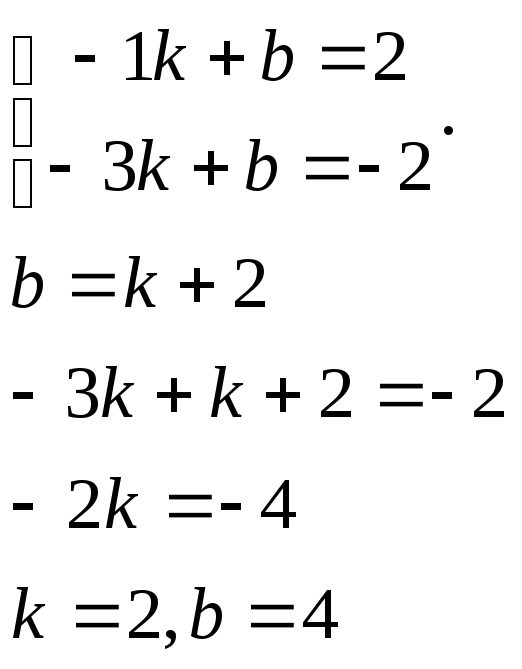
Подставим k,b уравнение. Ответ: y=2x+4

Задание 2.

Две стороны квадрата лежат на прямых 5x-12y-65=0 и 5x-12y+26=0 Вычислить его площадь.

А1=А2=5, значит прямые параллельны.

B1=B2=-12, A1/A2=B1/B2

Площадь равна квадрату расстояния между прямыми.

Определим произвольную точку М на прямой 5x-12y-65=0

Определим расстояние L от точки М до прямой 5x-12y+26=0

Подставляем М:

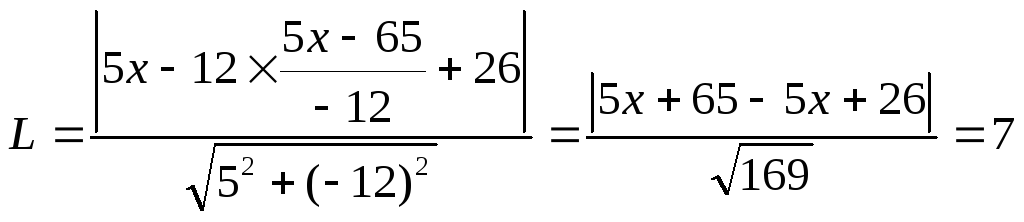
Площадь S = L² = 7² = 49 Ответ: 49.

Задание 3.

Записать общие уравнение плоскости, проходящий через перпендикуляры, опущенные из точек Р(-3,2,5) на плоскости

4x+y-3z+13=0 и x-2y+z-11=0.

Обозначим плоскости a,b,c.

a=4x+y-3z+13=0, b= x-2y+z-11=0, c=x_i+y_i+z_i+n_i=0

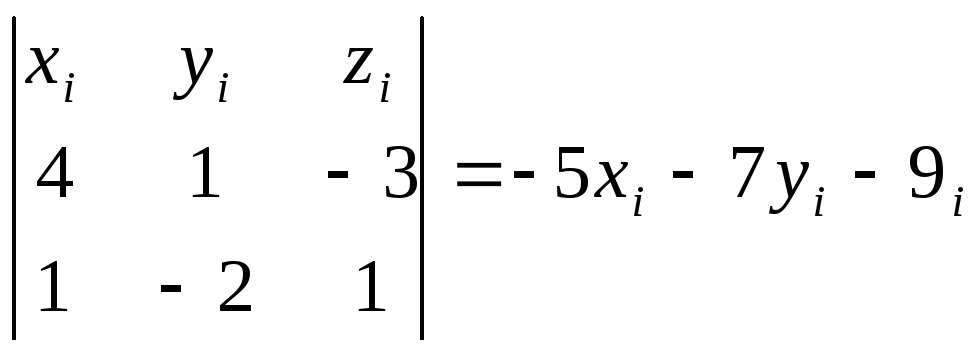
Подставляем Р(-3,2,5).

Ответ:

Задание 4.

Найти длину отрезка прямой, параллельной вектору I=(0,3,4), между точками пересечения её с плоскостями: 2x+y-z-6=0 и 2x+y-z-4=0.

Запишем уравнение прямой с вектором I=(0,3,4) и произвольной точкой M(x_i+y_i+z_i)

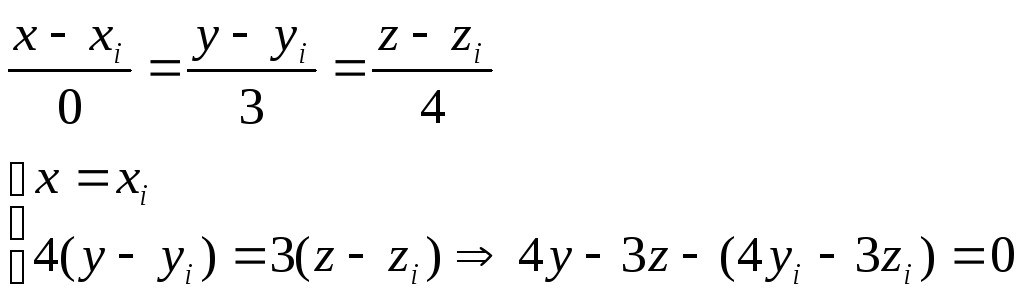
Тачка пересечения отрезка с 2x+y-z-6=0

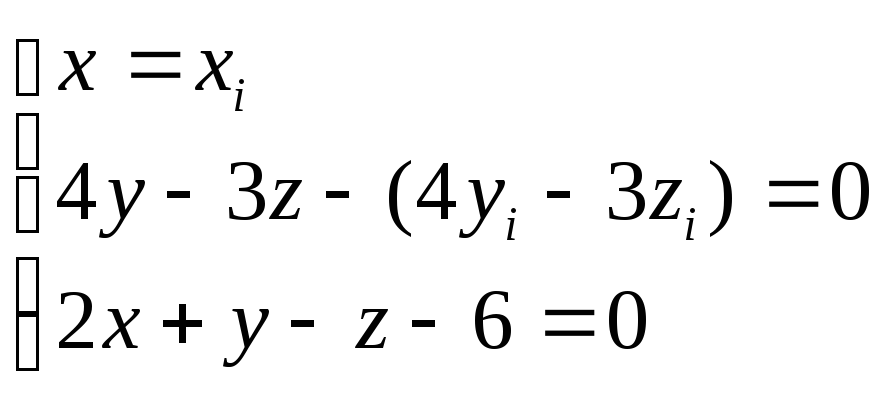
Выразим x,y,z.

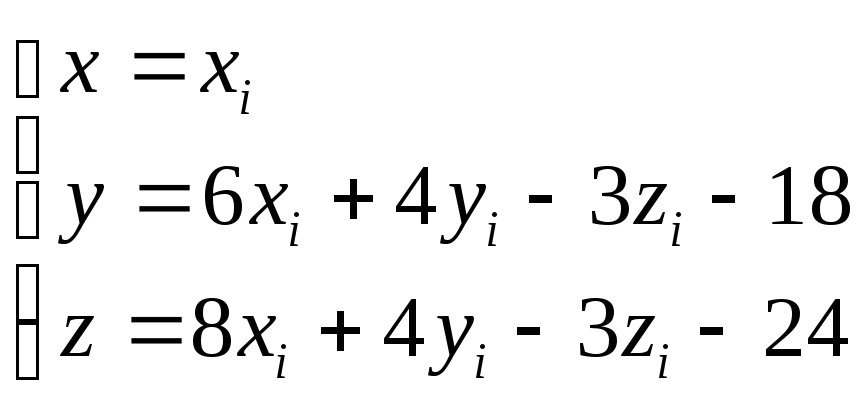
Тачка пересечения отрезка с 2x+y-z-4=0.

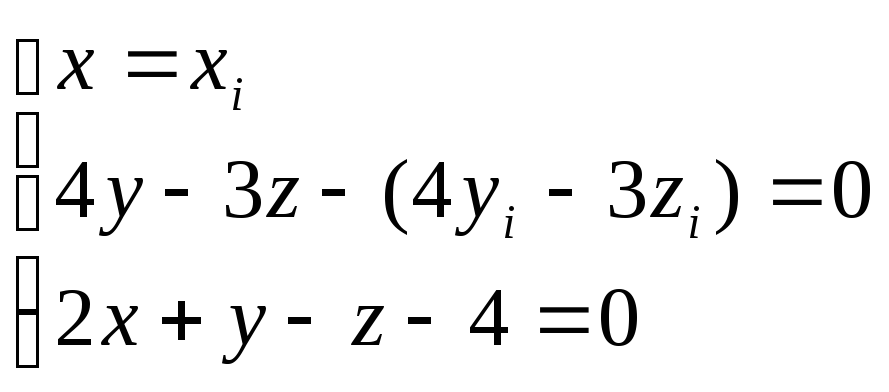
Выразим x,y,z.

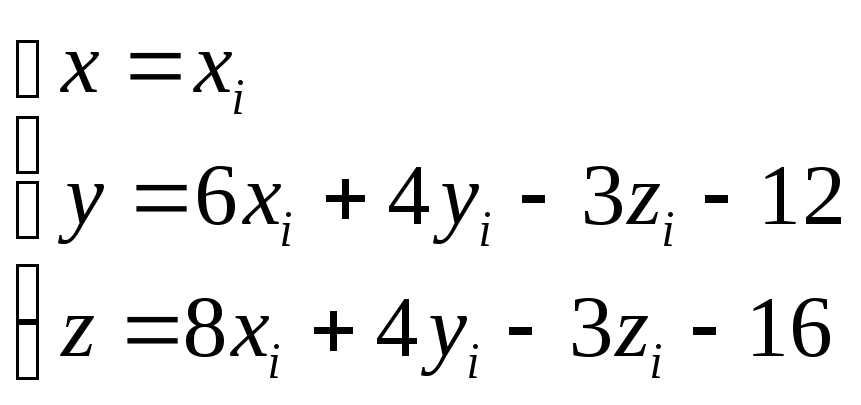
Ответ: АВ=10.

Задание 5.

Найти те значения m и n при которых прямая

пересекает прямые

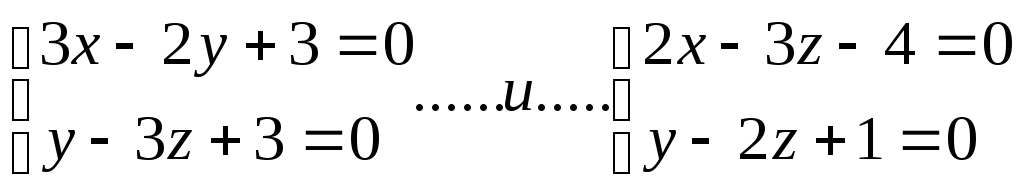
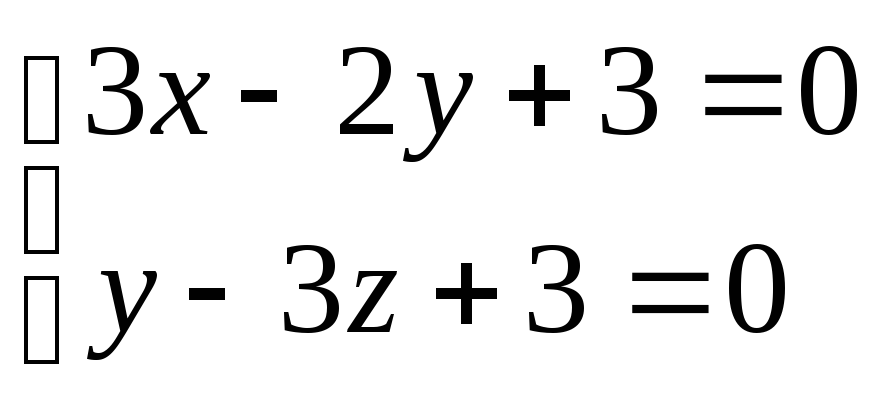присвоим х=0 ,

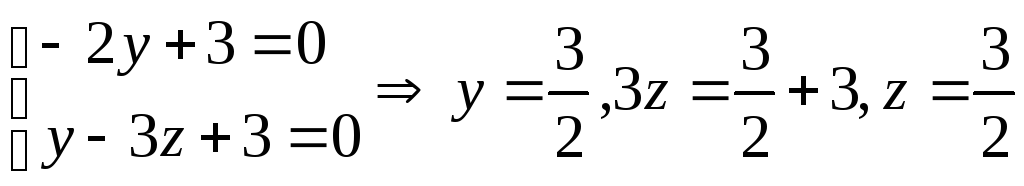
получили точку принадлежащей искомой прямой.

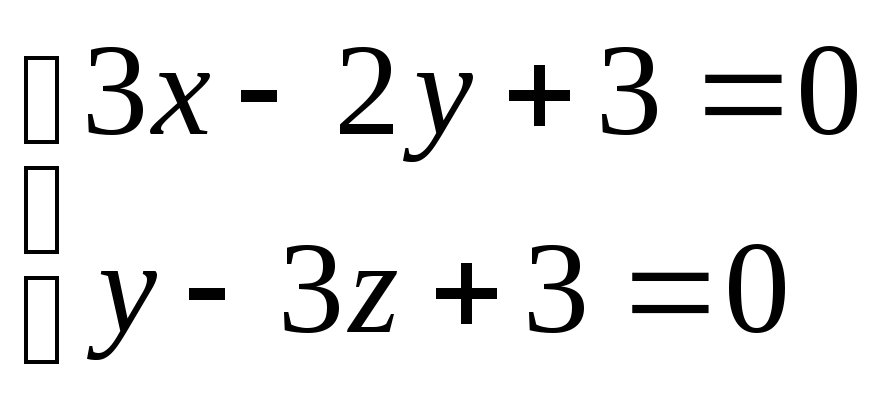присвоим y=0 ,

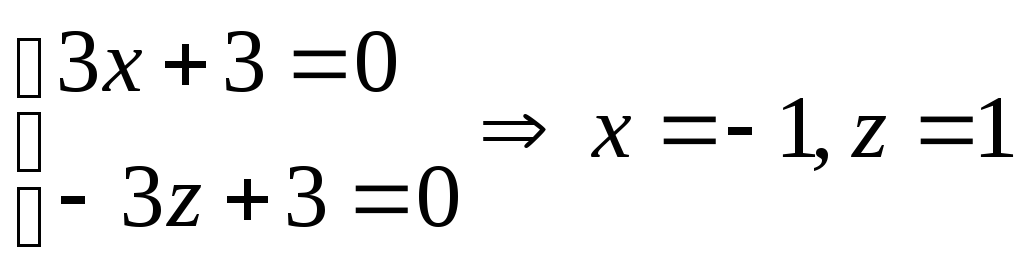
получили точку принадлежащей искомой прямой.

Уравнение прямой проходящей через эти точки имеет вид.

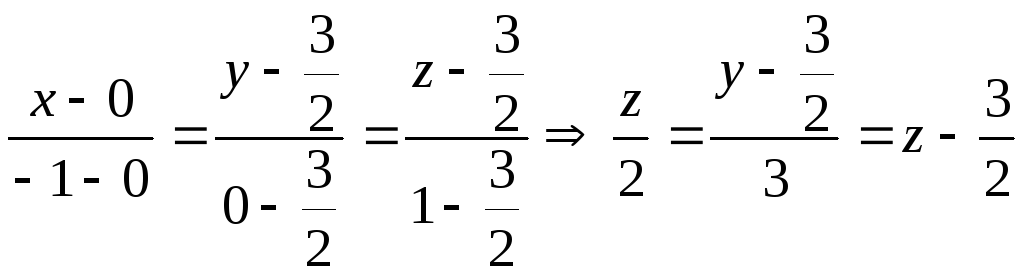
тоже самое для прямой

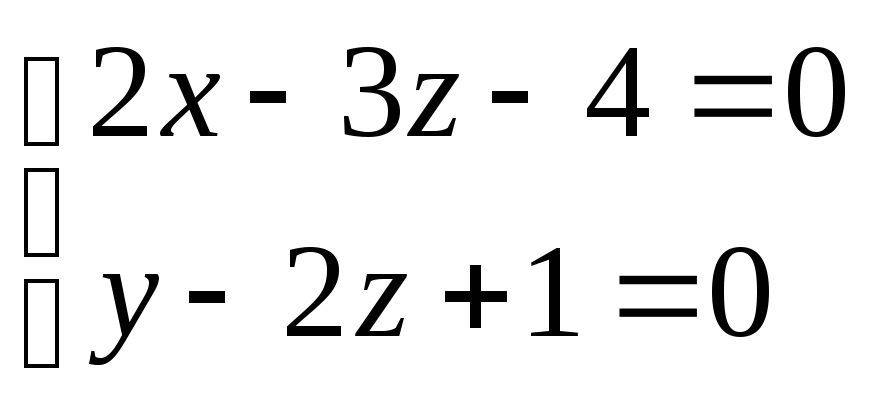присвоим х=0 ,

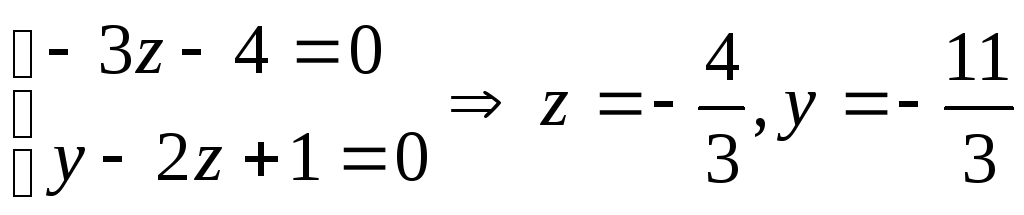
получили точку принадлежащей искомой прямой.

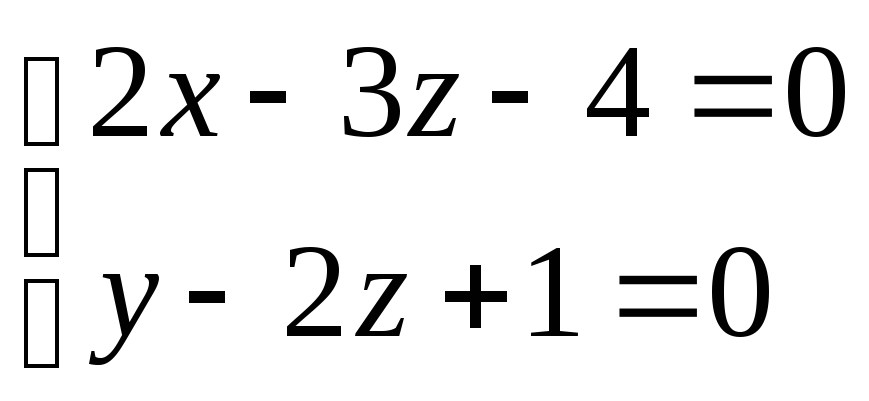присвоим z=0

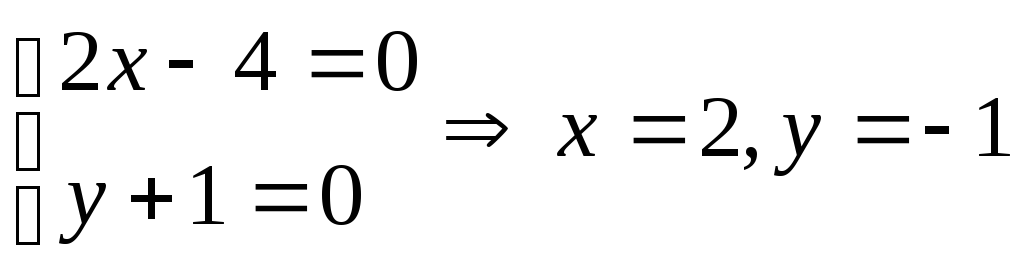
получили точку принадлежащей искомой прямой.

Уравнение прямой проходящей через эти точки имеет вид.

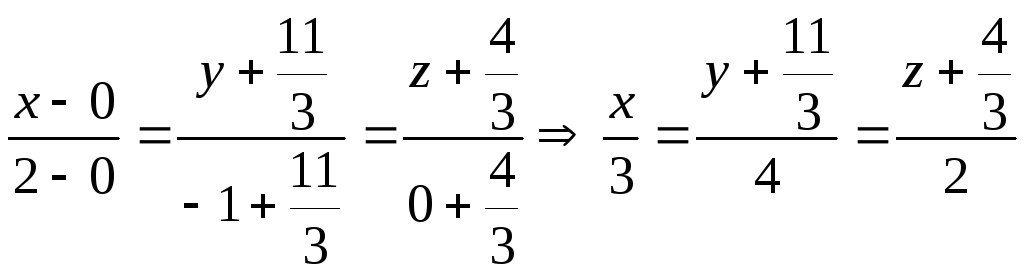
условие пересечения прямых имеет вид

. Тогда получим.

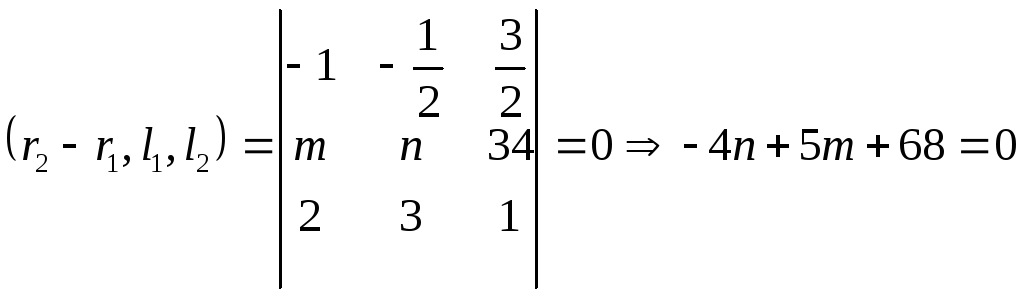
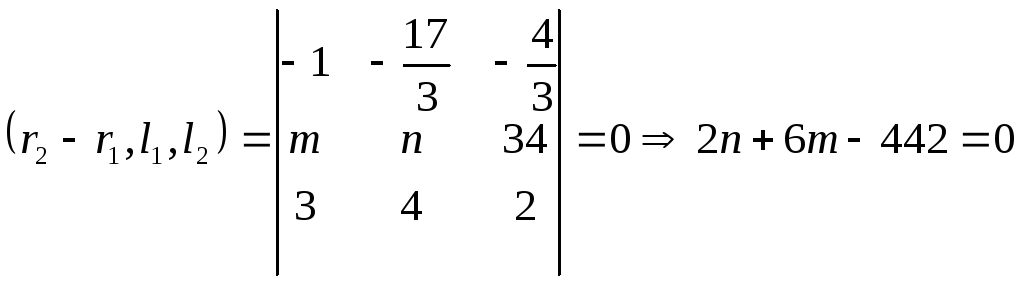
Решим эти два уравнения с помощью системы.

Ответ: n=77, m=48.

Задание 6.

Дано, что прямая, пересекающая ось аппликат в точке (0,0,Z₀),Z₀>0, параллельна плоскости 2x+3y+6z+7=0, отстоит от нее на расстоянии 7 и перпендикулярна оси ординат. Найти абсциссу точки пересечения этой прямой с координатой плоскостью z=0.

Ответ: x=21.

Задание 7.

Записать уравнение касательной к окружности x²+y²-4x+8y=17 в точке М(1,2).

Найдем центр окружности О.

Центр окружности О(2,-4).

Вектор нормали ОМ(-1,6).

Тогда получим уравнение…

x-6y+C=0.

1-6×2+C=0

C=11

x-6y+11=0

Ответ: x-6y+11=0

Задание 8.

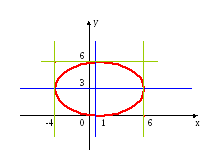
Дана кривая 9x²+25y²-18x-150y+9=0.

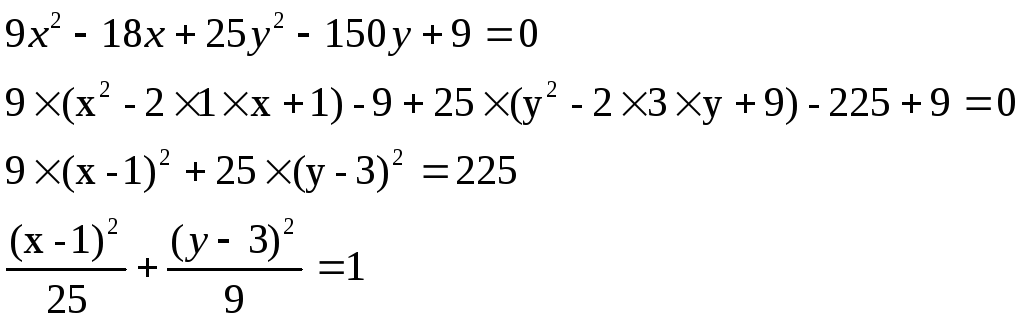
это эллипс с центром симметрии в точки (1,3)

большая полуось а=5

малая полуось б=3

уравнение фокальной оси y=3

Задание 9.

Дана кривая

x²-10x+2y+25=0

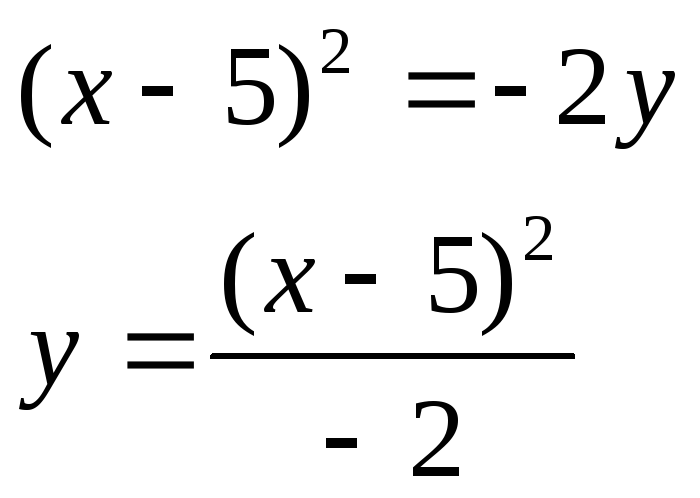
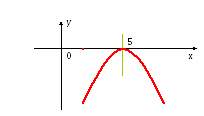
это парабола

вершина в точке (5,0)

р=-1

ось симметрии х=5.

Задание 10.

Дана кривая 15x²-20xy-70x+20y+135=0

Поделим все элементы на 5 и получим.

3x²-4xy-14x+4y+27=0

В(x,y) = 3 × x² + 2 × (-2) × x × y – 0 × y²

решаем характеристическое уравнение

собственные числа имеют разные значения поэтому эта кривая гипербола.

Собственные векторы матрицы В

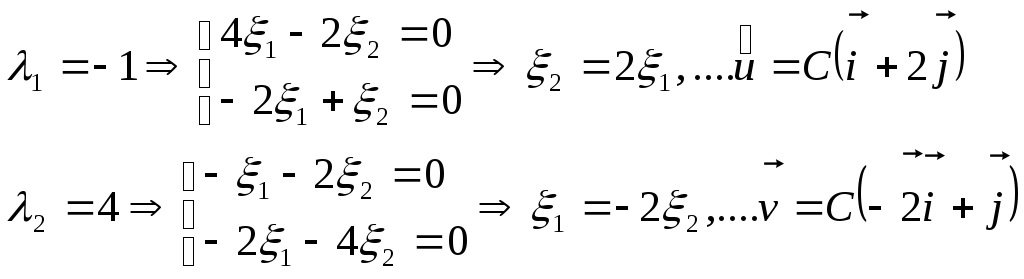
примем

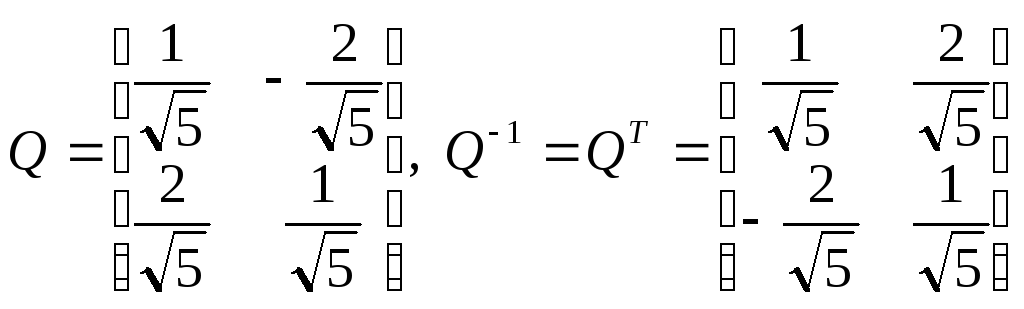
Определим координаты.

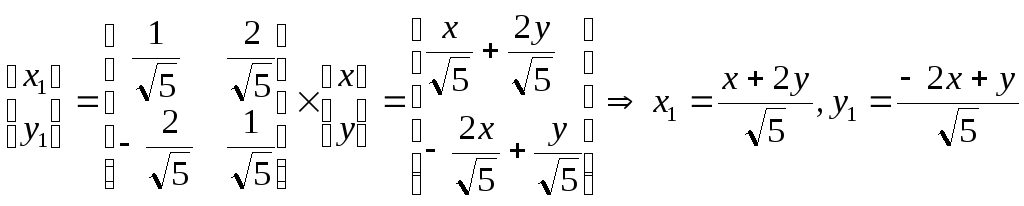
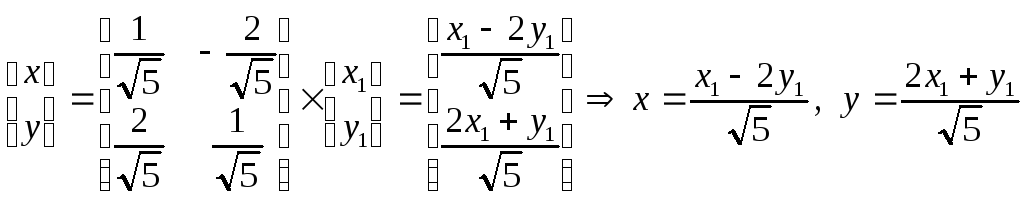
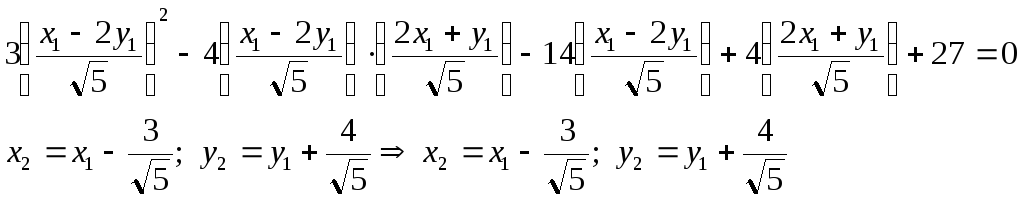
получим уравнение гиперболы.

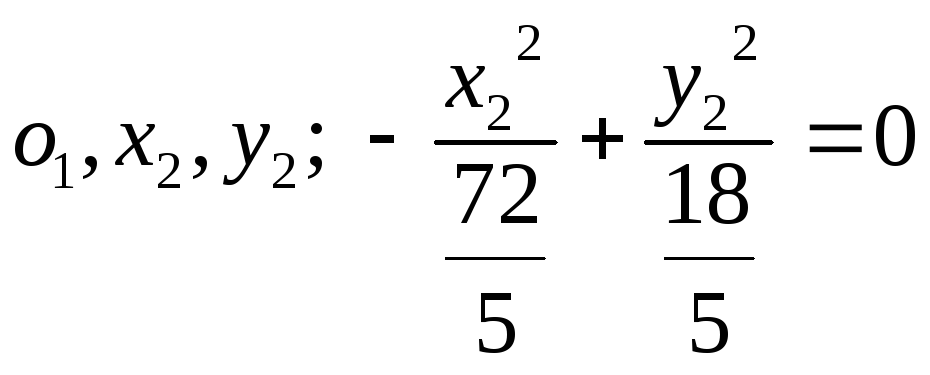
Уравнение оси O₁ X₁ x+2y+3=0, уравнение оси O₁Y₁ 2x-y-4=0

Координаты центра симметрии O₁.

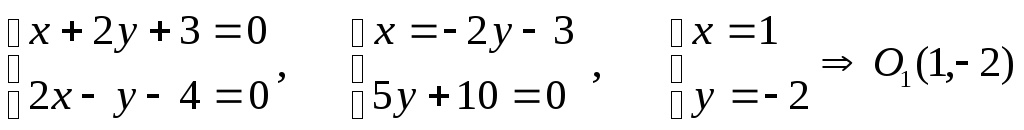
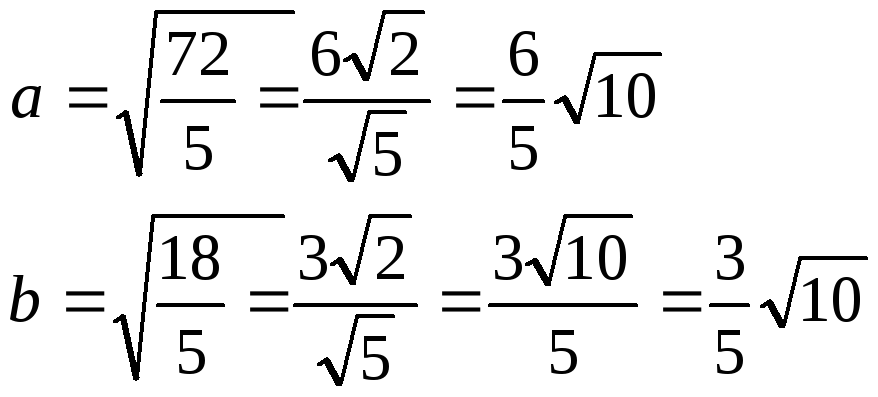
Уравнение фокальной оси 2x-y-4=0.

Начертим рисунок.