Контрольная работа 2 / 2- 2_Высшая математика_3

Томский межвузовский центр дистанционного образования

Томский государственный университет

систем управления и радиоэлектроники (ТУСУР)

Кафедра

Контрольная работа № 2

по дисциплине «Высшая математика»

Уч. Пособие Л.И. Магазинников,

А.Л. Магазинникова.

Выполнил:

студент ТМЦДО

специальности

Вариант 2.2

1. Запишите общее уравнение прямой, проходящей через точку

M₀ (2,-3) параллельную вектору , если А (4,5), В(3,-7).

Решение:

Следовательно, в качестве вектора нормали можно принять

12X-Y=(24+3)=0 или 12X-Y-27=0 – Искомое уравнение.

Ответ: 12X-Y=(24+3)=0

2. Стороны треугольника АВС заданы уравнениями АВ:

4x-y-7=0; BC: x+3y-31=0; AC: x+5y-7=0. Запишите общее уравнение высоты АН.

Решение:

Найдём координаты точки А.

Откуда:

A(2;1)

Высота проходит через точку A(2;1), перпендикулярно прямой

x+3y-31=0

В качестве вектора примем любой вектор, перпендикулярный вектору N=(1,3), например вектор

N₁=(3,-1)

3x-y-(6-1)=0 или

3x-y-5=0 – уравнение искомой высоты

Ответ: 3x-y-5=0

3) Запишите общее уравнение плоскости, проходящей через точки

M₁( 3,0,4) и M₂(1,1,0) перпендикулярно плоскости 2x+y+4z-7=0.

Решение:

Так как искомая плоскость проходит через точку

Параллельно вектору M₂M₁=(2,-1,4) и параллельно вектору нормали плоскости 2x+y+4-7=0 N=(2,1,4) то её уравнение

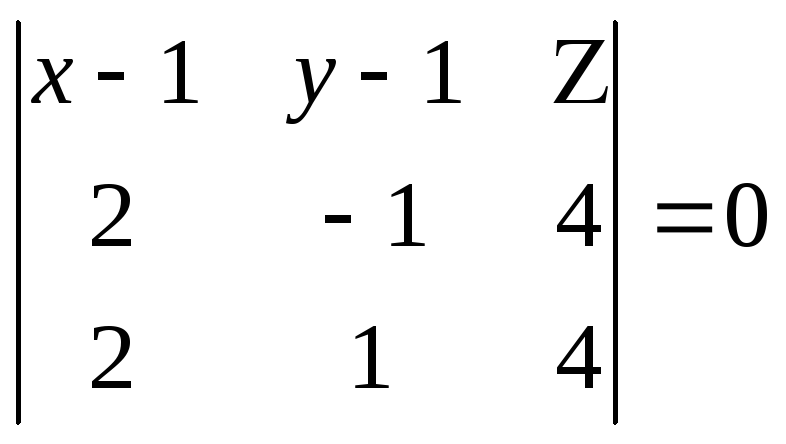
(x-2)(-4-4)-(y-1)(8-8)+Z(2+2)=0

2x-Z-2=0 – уравнение искомой плоскости.

Ответ: 2x-Z-2=0

4) Найдите расстояние от точки P(2,4,4) до прямой

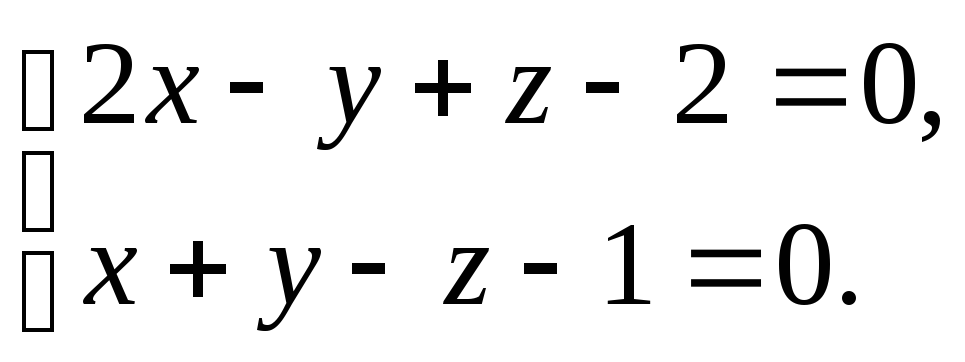
Решение: Найдём направляющий вектор прямой כ

Где N₁=(2,-1,1), N₂=(1,1,-1)

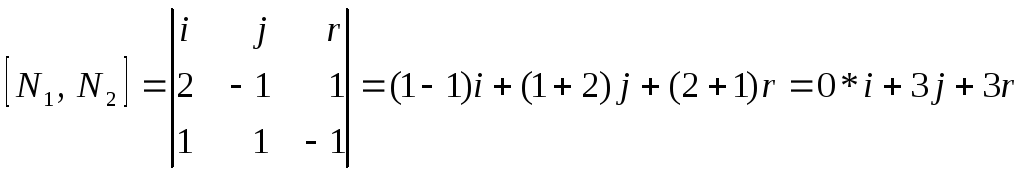
За вектор כ можно принять

כ=

Найдём точку Р₀(x₀,y₀,z₀), лежащую на данной прямой.

Пусть z₀=1, то x₀=1_, y₀=1

P₀(1,1,1)

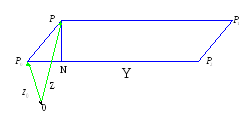
Искомое расстояние d равно высоте параллелограмма P₀ P P₁ P₂

d=

Найдём площадь параллелограмма

Y =Y =

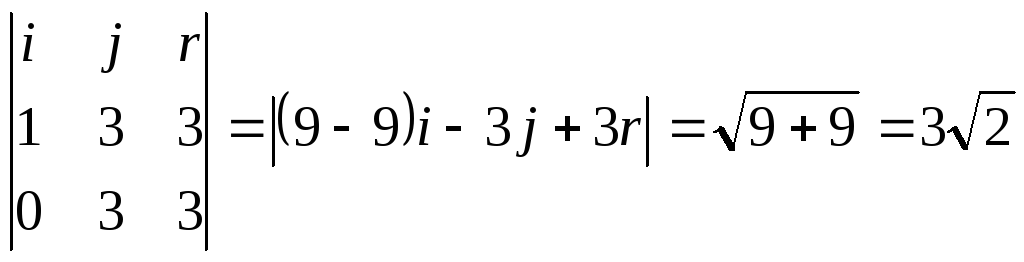
Найдём Y

Следовательно, d=

Ответ: 1

5) Плоскость проходит через прямую 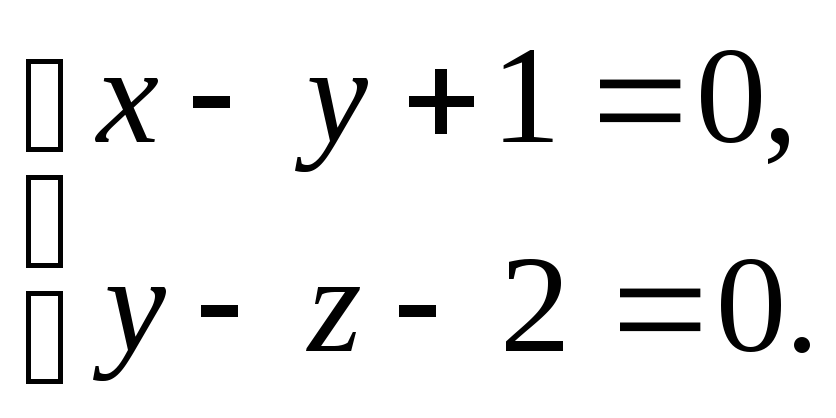параллельно вектору АВ=(8,4,7). Найдите длину отрезка, отсекаемого этой плоскостью от оси ординат.

Решение:

Плоскость П. параллельна направляющему вектору Y прямой и вектору , поэтому вектор N= является вектором нормали

плоскости.

Найдём вектор Y.

Разрешив данную систему относительно X и Z(y – свободное неизвестное ), получим ,Полагая y=t, Запишем параметрическое уравнение прямой

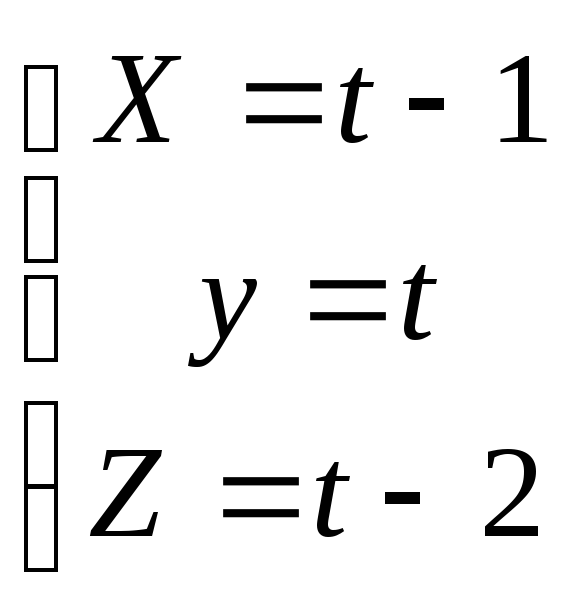
Y=(1,1,1) – направляющий вектор прямой

M₀ (-1, 0,-2) – лежит на прямой.

Находим

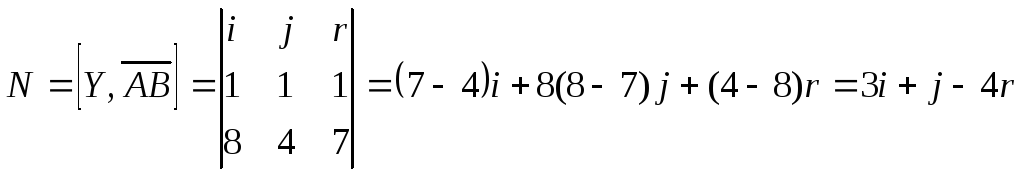
Запишем уравнение плоскости П 3x+y-4Z+D=0

Так как точка M₀(-1,0,-2) лежит на плоскости П, то

3(-1)+0-4(-2)+D=0

Откуда D=-5

Следовательно, 3x+y-4Z-5=0 – Уравнение плоскости П.

Так как искомая точка лежит на оси ординат, то x=Z=0

Откуда y=5

Ответ: 5

6) Две прямые, пересекающиеся в точке P(0,0,z₀), z₀>0

параллельны плоскости 2x+y+2z+6=0 и отстают от неё на расстояние 4. Одна из прямых пересекает ось абсцисс, а вторая – ось ординат. Найдите тангенс острого угла между ними.

Решение:

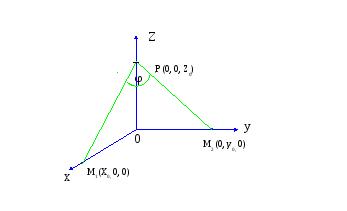
Одна из прямых проходит через точки Р(0,0,Z₀) и M₁(X₀,0,0)

Вторая – через точки P(0,0,Z₀) и M₂(0,y₀,0), Поэтому их направляющими векторами Y₁ и Y₂ являются векторы

Следовательно, Y₁=(x₀, 0, -Z₀), Y₂=(0, y₀, -Z₀)

По условию задачи векторы Y₁ и Y₂ параллельны плоскости

2x+y+2Z+6=0, т.е. перпендикулярны вектору N(2,1,2), поэтому

(Y₁, N)=0 и (Y₂, N)=0

Т.е. 2x₀-2Z₀=0 и y₀-2Z₀=0

Так как прямые PM₁ и PM₂ параллельны плоскости 2x+y+2Z+6=0

И отстают от неё на расстояние 4, то точка Р – их пересечения отстоит от плоскости на это же расстояние

Откуда Z₀=6

Получим систему

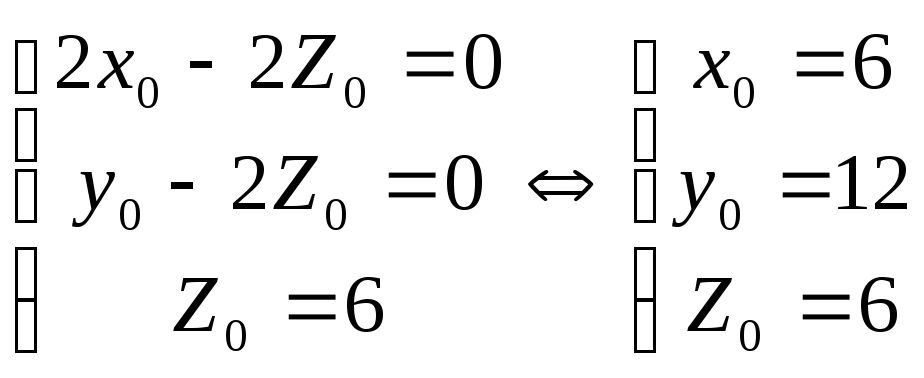
Таким образом, Y₁=(6, 0, -6)

Y₂= (0, 12, -6)

Находим косинус угла между векторами Y₁ и Y₂

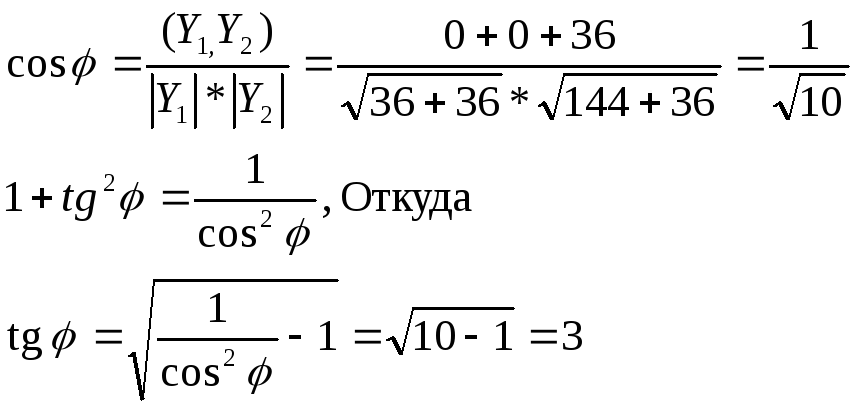
Ответ:

7) Найдите радиус окружности с центром в точке M(2,4), если известно, что прямая 3x+4y+8=0 касается этой окружности.

Решение

Так как радиус, проведённый в точку касания перпендикулярен касательной, то он равен расстоянию от центра окружности M(2,4)

до прямой 3x+4y+8=0

Ответ: R=6.

8) Дана кривая 25x²+16y²-150x-32y-159=0.

8.1) Докажите что эта кривая – эллипс.

8.2) Найдите его большую и малую полуоси.

8.4) Запишите уравнение фокальной оси.

8.5) Постройте данную кривую.

1. Преобразуем данное уравнение, выделив полные квадраты.

Введём новые координаты

x₁=x-3, y₁=y-1, тогда разделив обе части уравнения на 400 получим

- Это уравнение определяет эллипс.

2. Точка 0₁(3,1) – центр симметрии эллипса.

3. Большая полуось b=5, малая полуось а=4

4. Фокальная ось проходит через центр симметрии эллипса, параллельно оси ординат x=3 – её уравнение.

5. Построим эллипс

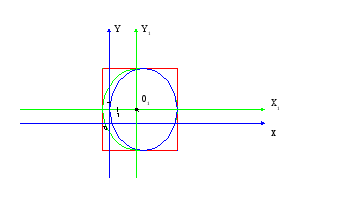
9) Дана кривая y²-2y+4x+9=0.

9.1) Докажите что данная кривая – парабола.

9.2) Найдите координаты её вершины.

9.3) Найдите значение её параметра p.

9.4) Запишите уравнение её оси симметрии.

9.5) Постройте данную параболу

Решение

1. Приведём уравнение кривой к каноническому виду

Y²-2y+1=-4x-8

(y-1)²=-4(x+2)

Положим y₁=y-1, x₁=x+2, тогда получим y₁²=-4x₁ – это уравнение параболы

2. Точка 0,(-2, 1) – вершина параболы

3. 2p=-4, p=-2 –параметр параболы

4. y-1=0 – уравнение оси симметрии

5. Построим параболу.

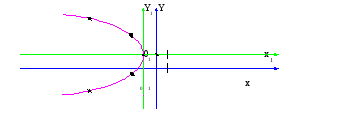
10) Дана кривая x²-7y²-6xy+2x+26y+57=0.

10.1) Докажите что эта кривая – гипербола.

10.2) Найдите координаты её центра симметрии.

10.3) Найдите действительную и мнимую полуоси.

10.4) Запишите уравнение фокальной оси.

10.5) Постройте данную гиперболу.

Решение:

1. Квадратичную форму приводим к главным осям. Для этого записываем матрицу этой квадратичной формы B= 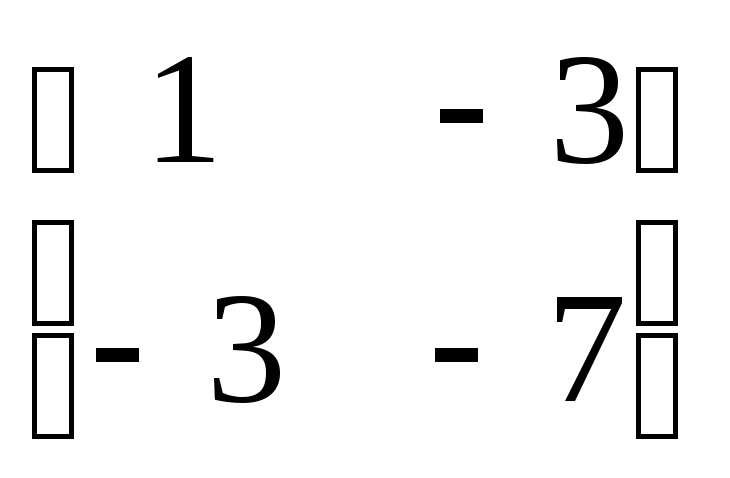и находим её собственные числа и собственные векторы. Записываем и решаем характеристическое уравнение матрицы В:

Так как λ₁*λ₂<0, то уравнение определяет гиперболу

II) Чтобы ответить на остальные вопросы задачи, приведём уравнение к каноническому виду. Находим собственные векторы для собственного числа λ=-8

Получаем:

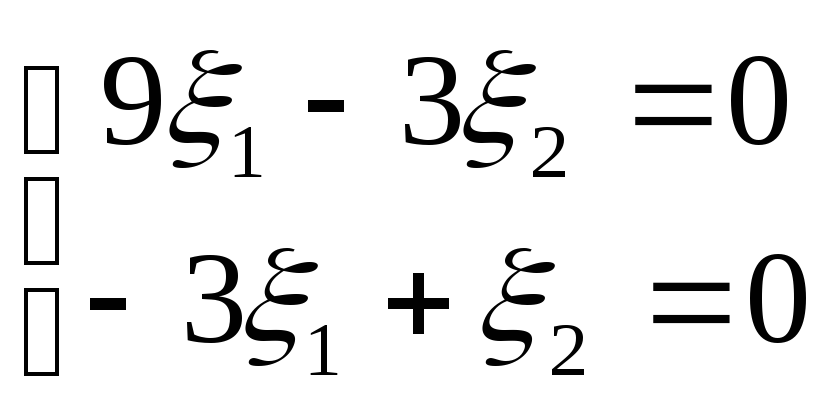, отсюда, Полагая , найдём единичный вектор

Второй собственный вектор имеет вид

От старого базиса (0, i, j ) перейдём к новому базису (0₁, i₁, j₁ )

Матрица перехода имеет вид

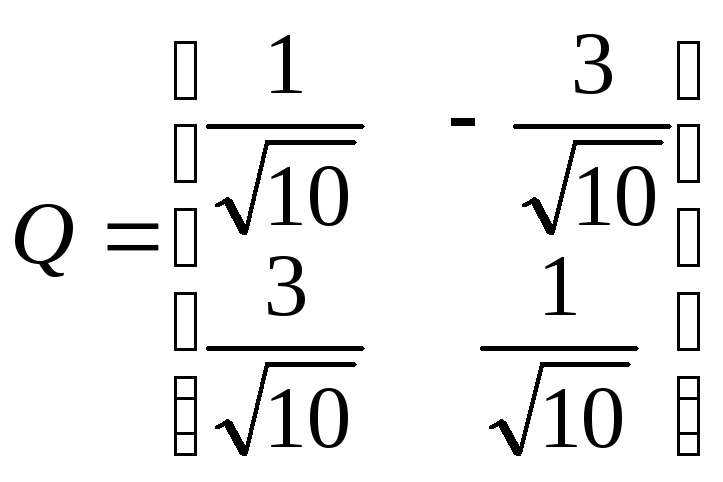
Обратная матрица

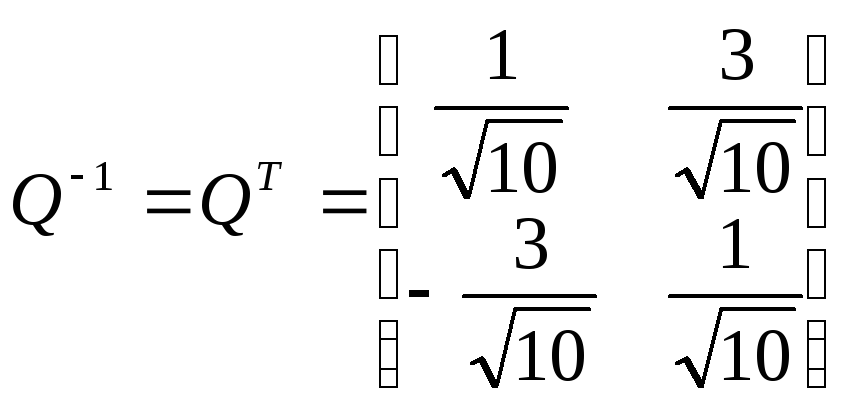
Старые координаты связаны с новыми соотношениями

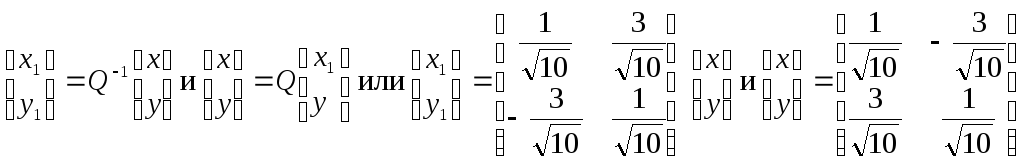
Откуда

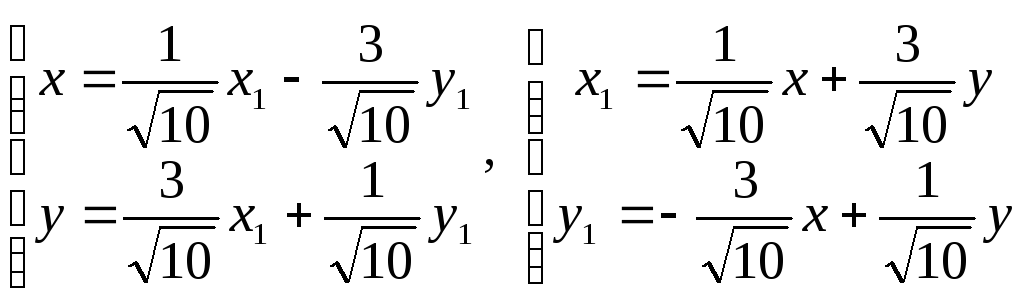
В новой системе координат уравнение данной кривой имеет вид:

Выделим полные квадраты:

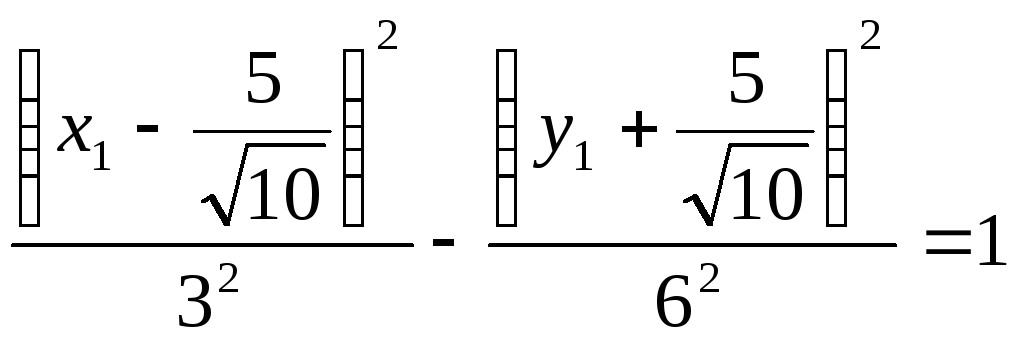
Совершим параллельный перенос осей координат в новое начало 0₁ по формулам:

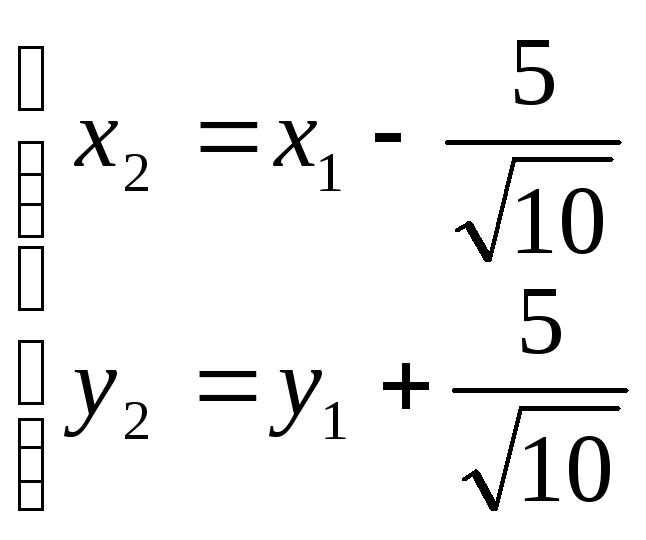Теперь в системе координат (0₁, i₁, j₁) гипербола имеет уравнение

II) Точка 0₁ – центр симметрии гиперболы.

Найдём его координаты:

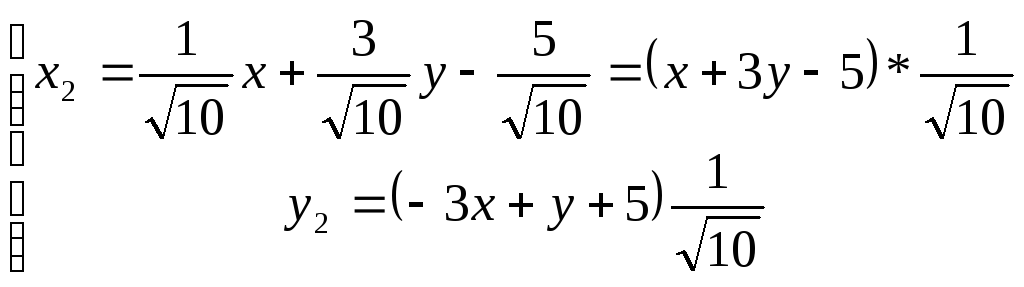
Решим систему

Получаем 0₁(2, 1)

III)Действительная полуось a=3, мнимая b=6.

IV) Фокальной осью является прямая y₂=0, -3x+y+5=0 или 3x-y-5=0

V)Для построения гиперболы в старой системе координат строим первую систему. Оси 0₁x₂ и 0₁y₂ направлены по прямым x+3y-5=0 и 3x-y-5=0

13