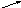Контрольная работа 2 / 2- 7_Высшая математика (Математика Ерохина Байбакова КР 2 вар 7)
.doc
y/ = 1- 4![]() =
1-
=
1-
![]() ;
;
y/ = 1-
![]() ;
y/ = 0 при х = 4
;
y/ = 0 при х = 4
х = 4 – критическая точка на отрезке [1,9].
Вычислим значение функции на концах отрезка и в критической точке:
у1(1) = 1 – 4![]() +
5 = 1 – 4 + 5 = 2; у2(1) =1 + 4 + 5 = 10
+
5 = 1 – 4 + 5 = 2; у2(1) =1 + 4 + 5 = 10
у1(4) = 4 – 4![]() +
5 = 4 – 8 + 5 = 1; у2(4) =4 + 8 + 5 = 17
+
5 = 4 – 8 + 5 = 1; у2(4) =4 + 8 + 5 = 17
у1(9) = 9 – 4![]() +
5 = 9 – 12 + 5 = 2; у2(9) =9 + 12 + 5 = 26.
+
5 = 9 – 12 + 5 = 2; у2(9) =9 + 12 + 5 = 26.
у = 1 – наименьшее значение функции
у = 26 – наибольшее значение функции
на отрезке [1,9].
10. Проведите
полное исследование функции у
=
![]() и постройте ее график.
и постройте ее график.
Решение:
у =
![]()
1. Функция определена во всех точках, кроме х = 3
2. Функция не периодическая, не симметрична относительно оси координат
3. у = 0 при
![]() = 0
= 0
Д = 36 - 3![]() 4
= 24
4
= 24
Х1,2 =
![]() ;
Х1 = 3 +
;
Х1 = 3 +![]() ;
Х2 = 3 -
;
Х2 = 3 -![]() -
точки пересечения с осями координат
-
точки пересечения с осями координат
4. Функция имеет разрыв второго рода в точке х = 3
![]()
![]() ;
;
![]()
![]()
Прямая х = 3 – вертикальная асимптота.
5. Исследование на экстремумы
y/ =
![]()
y/ =
![]() ;
y/ =
;
y/ =
![]()
y/ =
![]()
Приравниваем y/ к нулю:
y/ = 0 при
![]() = 0
= 0
Д < 0 – корней нет
y/ ≠ 0 при любых значениях х
Экстремумов нет.
y/ > 0 при
![]() > 0
> 0
т.к. (х – 3)4> 0 при любых х ≠ 3
х
![]() (-
(-![]() ;
3 ) – функция возрастает
;
3 ) – функция возрастает
х
![]() (3; +
(3; +![]() )
– функция возрастает
)
– функция возрастает
6. Исследование на выпуклость и вогнутость.
Найдем вторую производную:
y// =
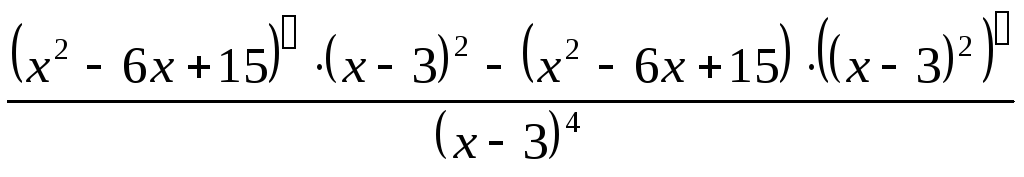
y// =
![]()
y// =
![]()
y// =
![]()
y// = -
![]() ;
y// = -
;
y// = -
![]()
y// = 0 при x = 3, следовательно:
![]() >
0 при любых х ≠ 3
>
0 при любых х ≠ 3
y// > 0 при
![]() <
0; х< 3- вогнутость
<
0; х< 3- вогнутость
y//< 0 при
![]() >
0; х> 3- выпуклость
>
0; х> 3- выпуклость
x = 3 – точка перегиба
|
x |
(- |
3 |
(3; + |
|
y/ |
+ |
0 |
+ |
|
у |
|
не определена |
|
|
функция |
возрастает |
разрыв второго рода |
возрастает |
|
y// |
вогнутость |
точка перегиба |
выпуклость |
7. Наличие асимптот
x = 3 – вертикальная асимптота
установлено выше.
Найдем наклонные асимптоты в виде у = k х +в:
k =![]()
![]() ;
в =
;
в =
![]() [y
– kx];
[y
– kx];
k =![]()
![]()
![]()
![]()
![]()
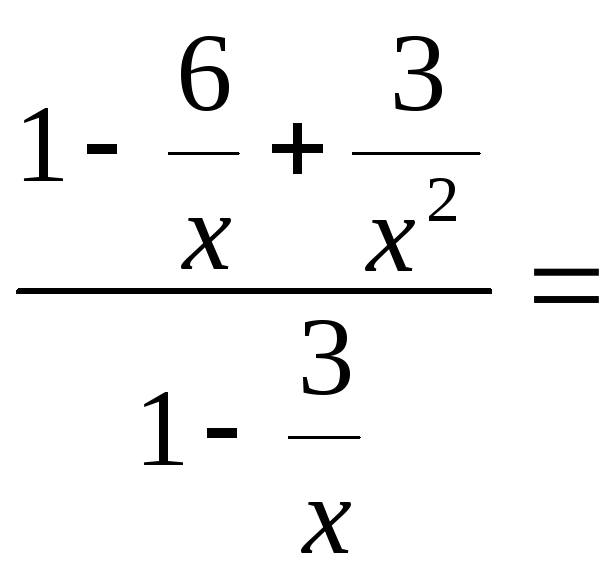 1
1
k = 1
в =
![]() [y
– kx] =
[y
– kx] =
![]()
![]()
![]()
![]()
![]()
![]()
![]()
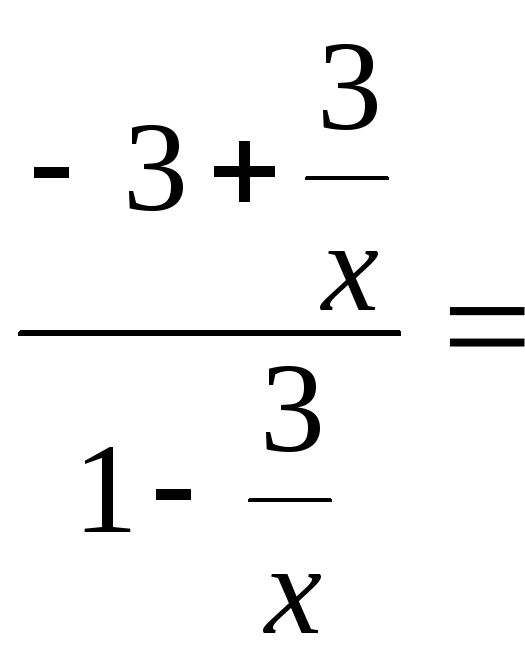 - 3
- 3
в = - 3
y = x – 3 - уравнение наклонной асимптоты
8.Дополнительные точки
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
y |
-5 |
|
-2,5 |
-1 |
1 |
5 |
±∞ |
-5 |
-1 |
1 |
2,5 |
|
9. Строим график функции по имеющимся данным: