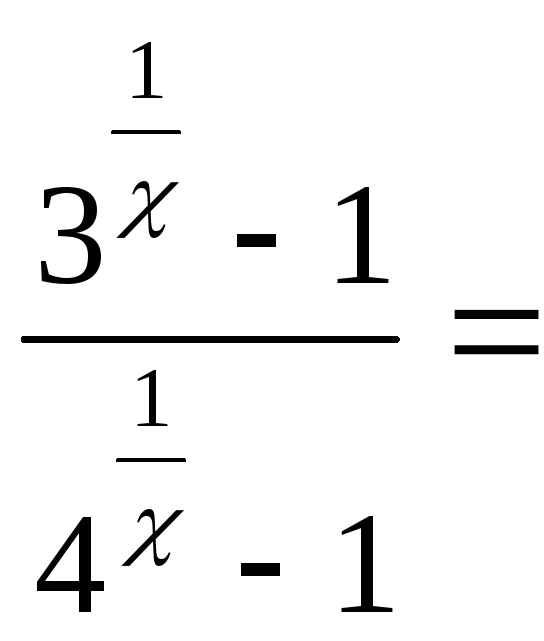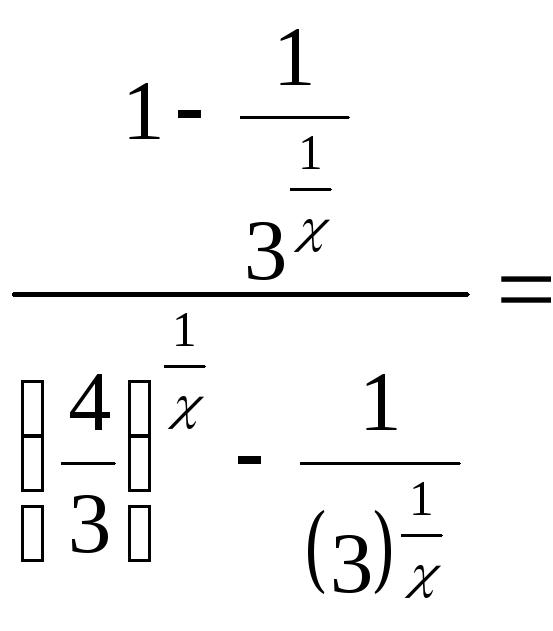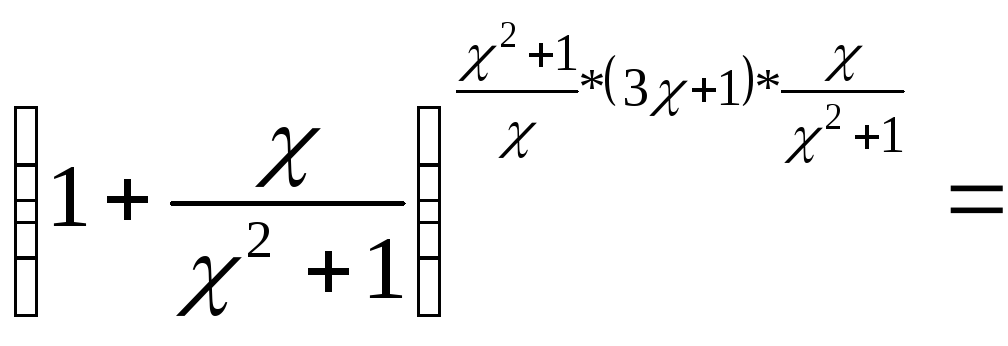Контрольная работа 2 / 2- 1_Высшая математика_9
.doc
 Текстовая контрольная работа по
математике.
Текстовая контрольная работа по
математике.
Контрольная работа N 2.
Вариант 1.
Учебное пособие Высшая математика Часть 1
Ерохина А.П., Байбакулова Л.Н.
Бортникова Наталья Викторовна. Uc061bnv 18453615
г.Удачный.
Республика Саха-Якутия, Мирнинский район, Н-город 21-117
1.Найдите пределы последовательностей:
а)
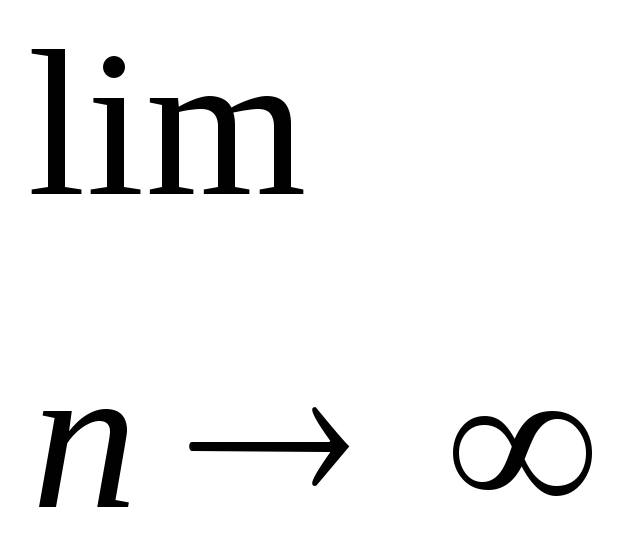

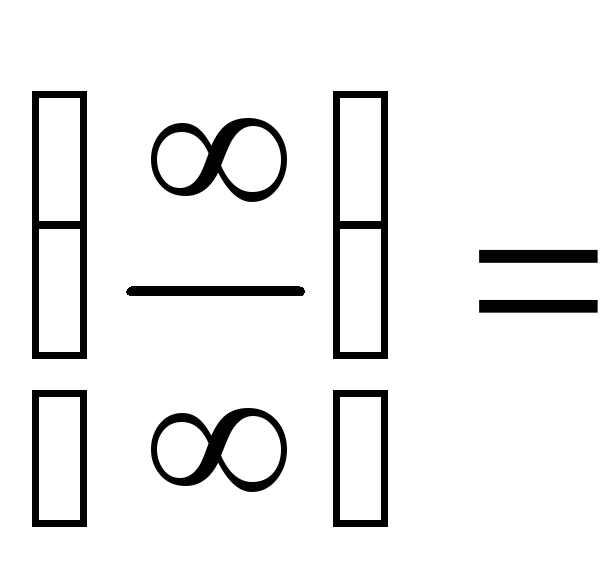
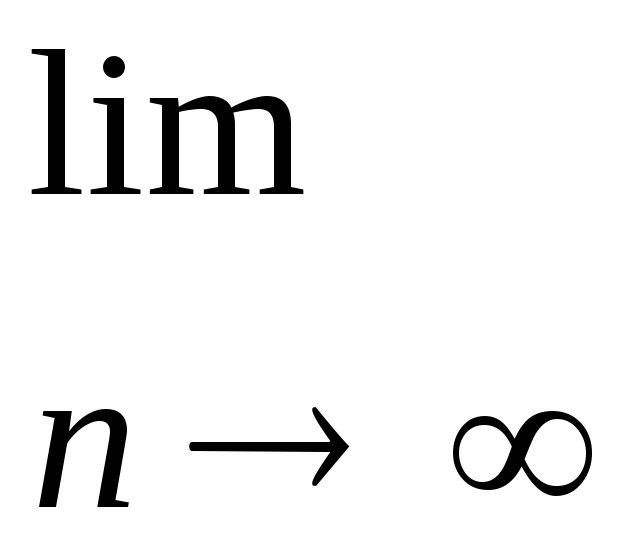
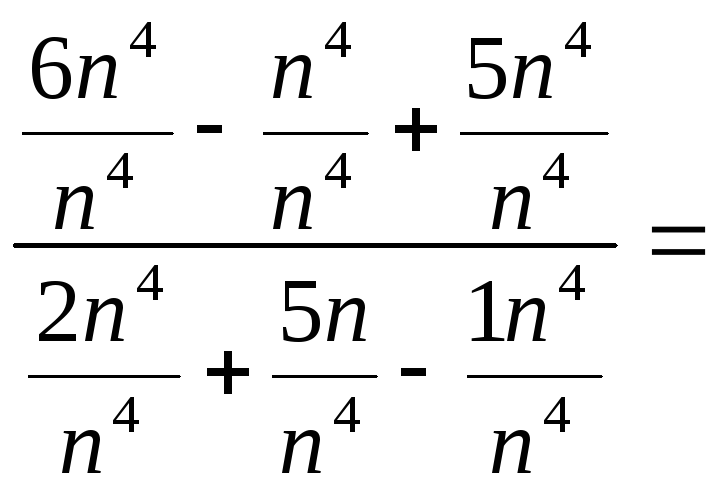
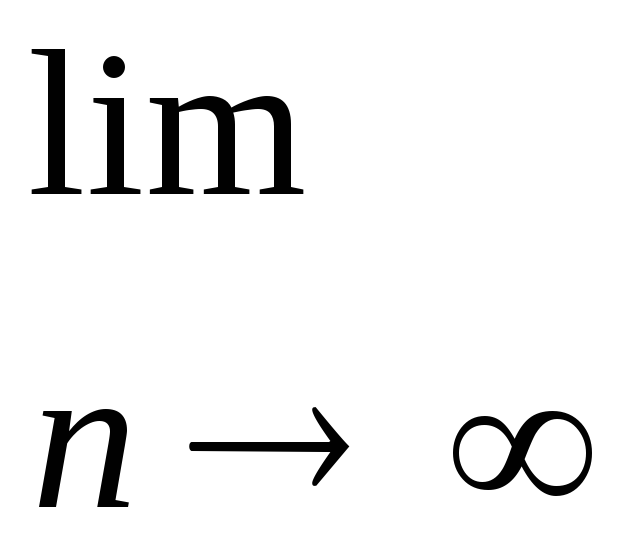
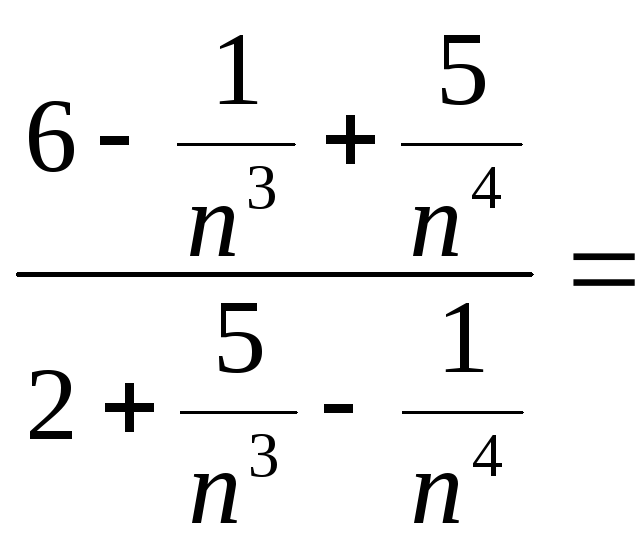
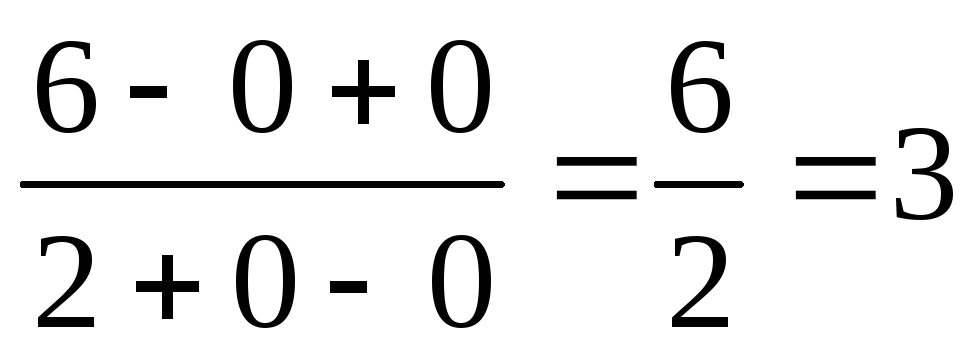 .
.
б)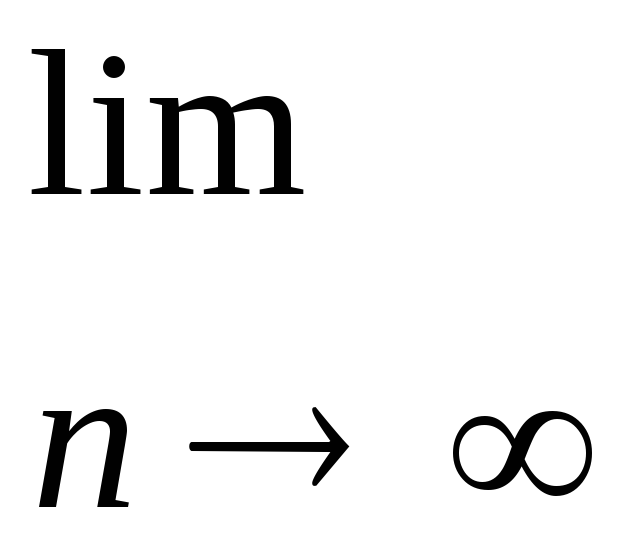
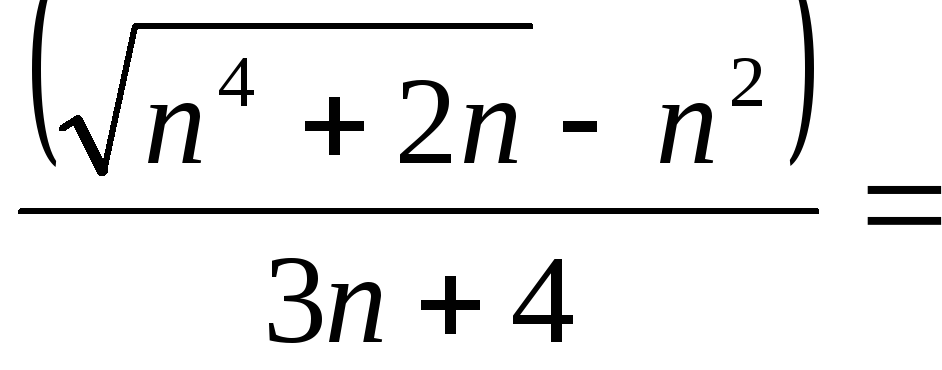
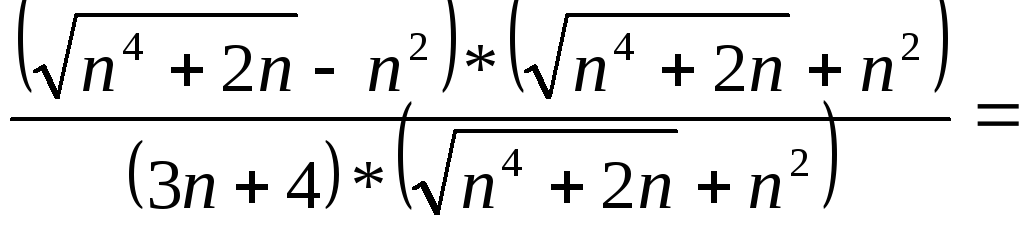



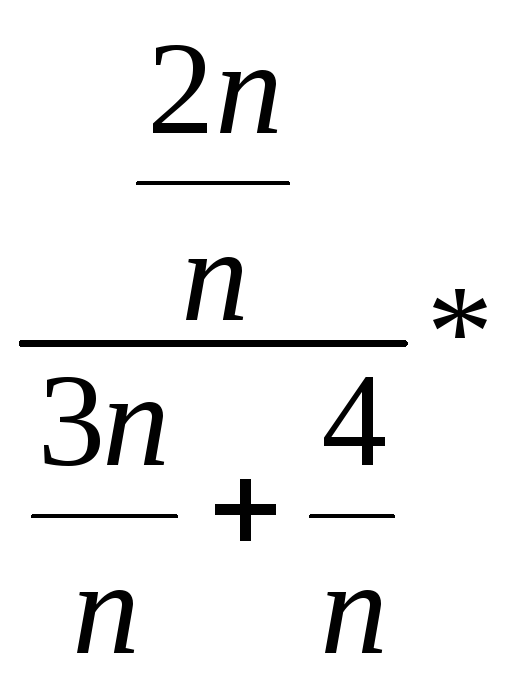
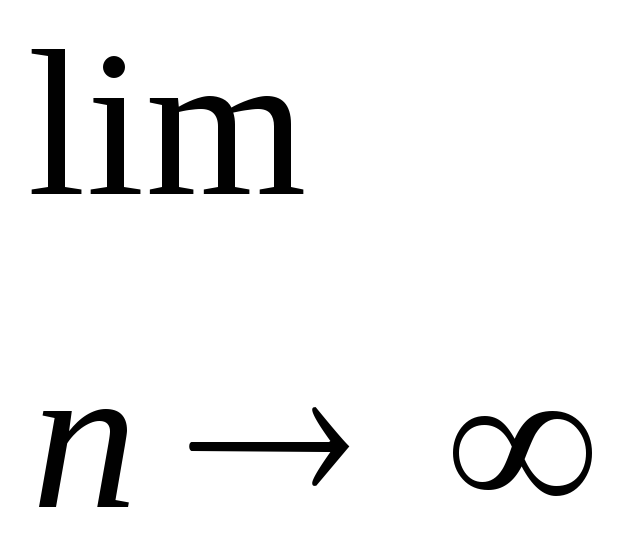


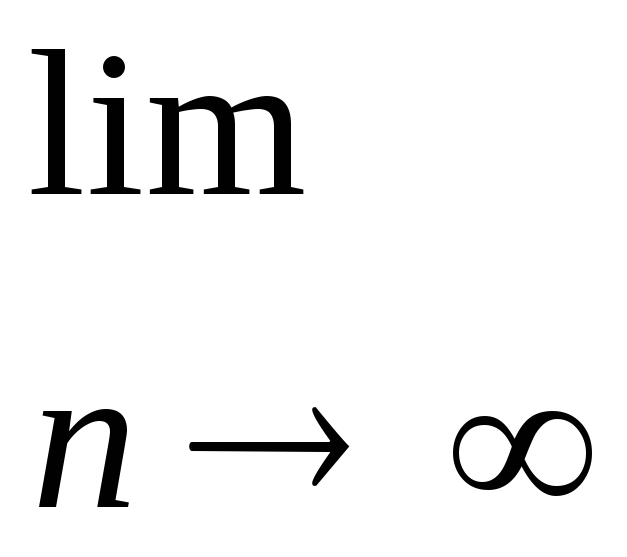
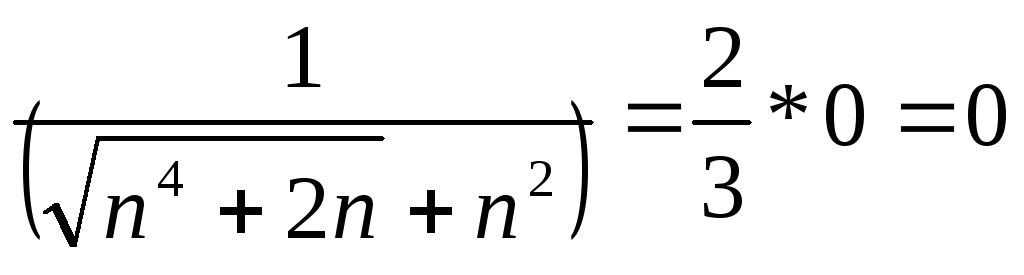 .
.
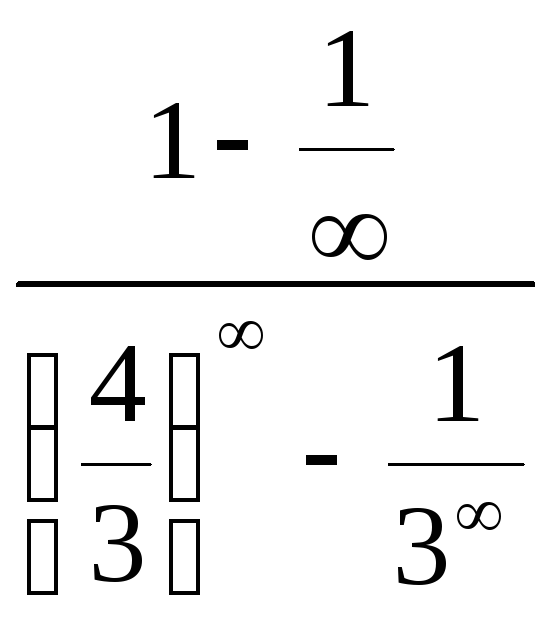
2.Найдите
пределы функций:
а)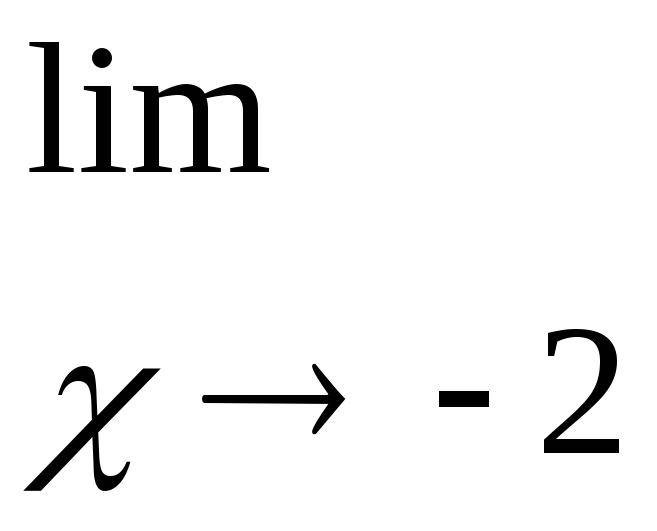
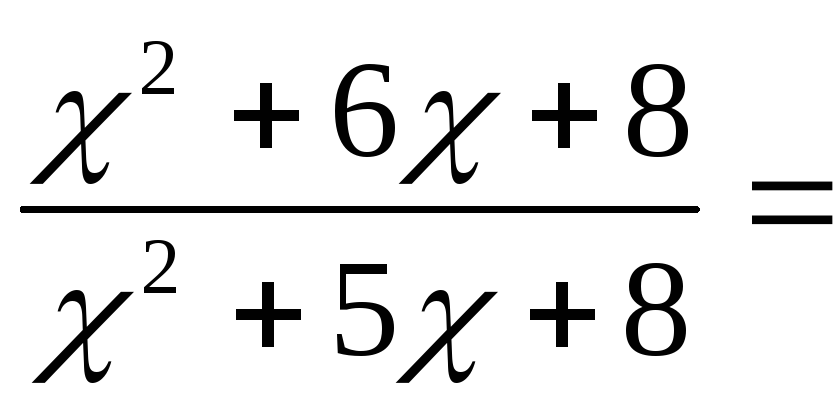
![]()
![]()
![]()
![]()
![]()
![]()
=![]()
![]()
б)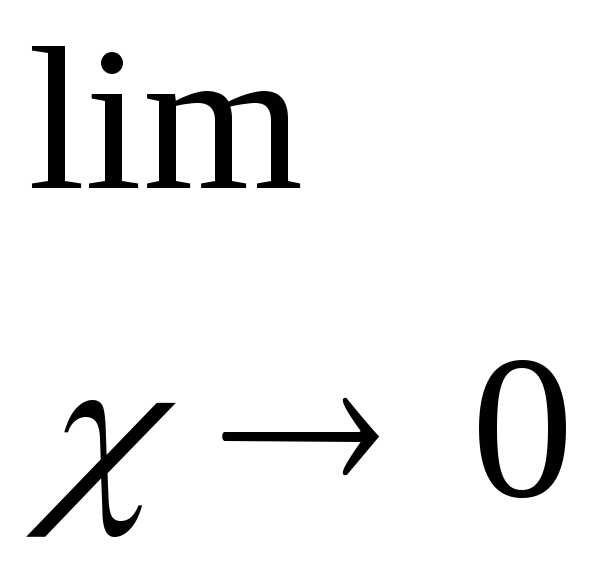
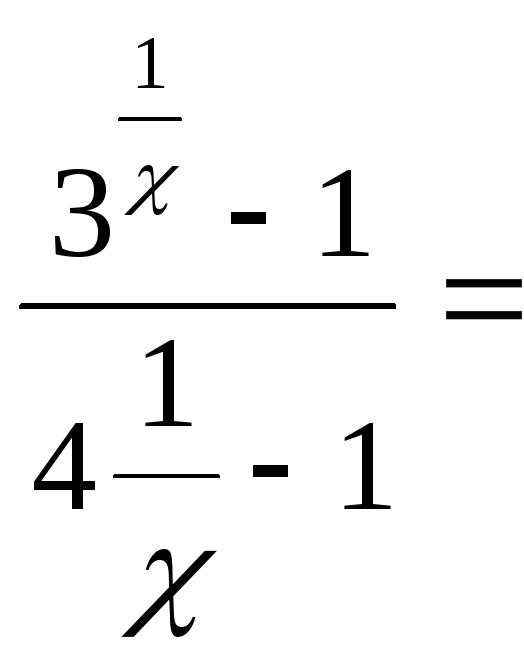
найдём односторонние пределы:
![]()
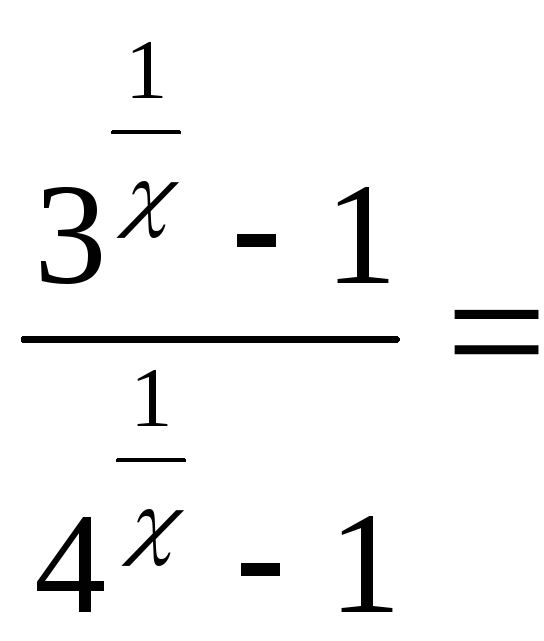
![]()
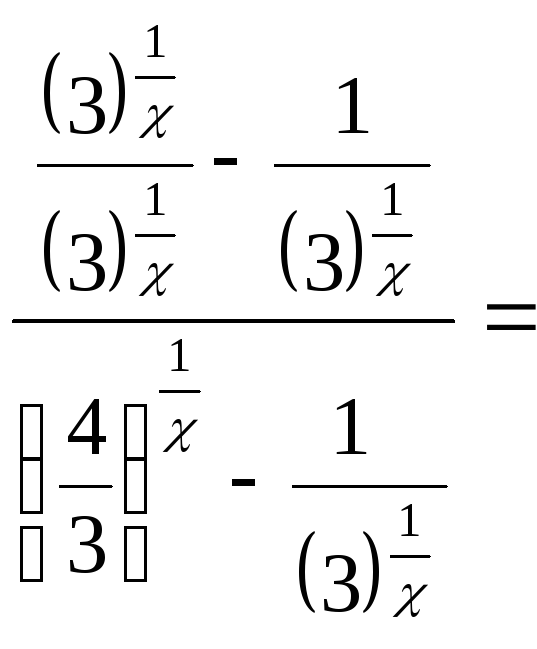
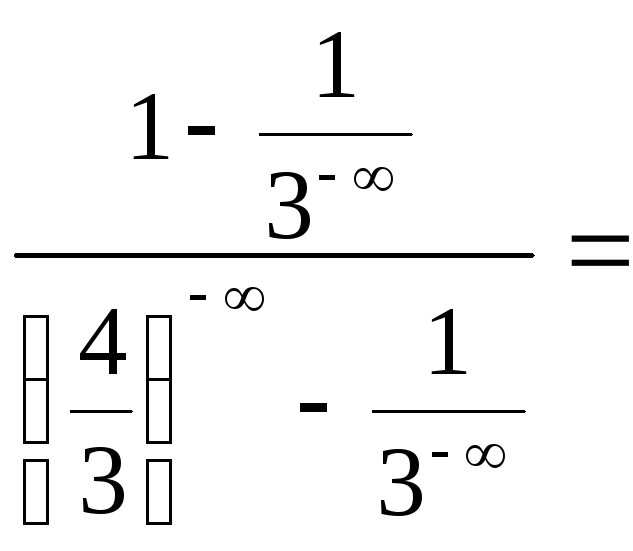
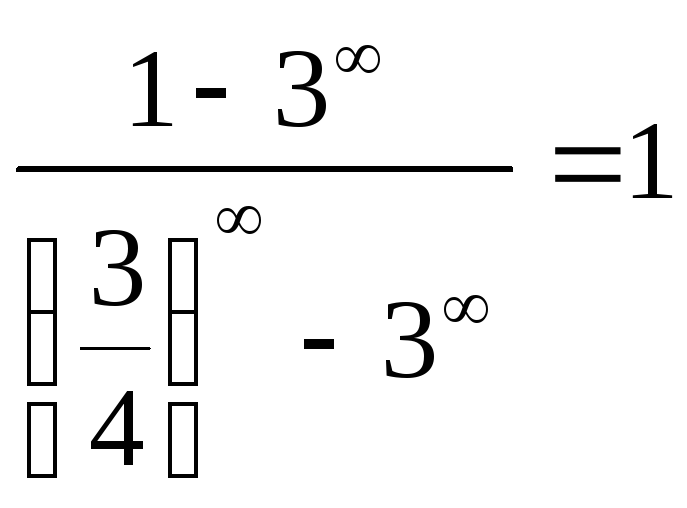
![]()
![]()
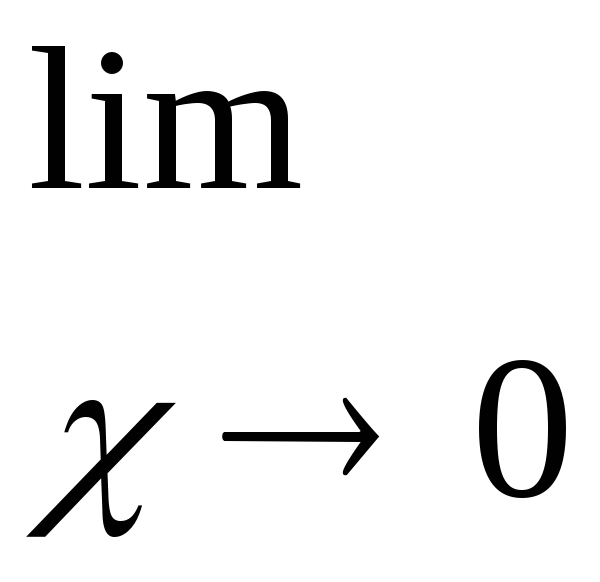
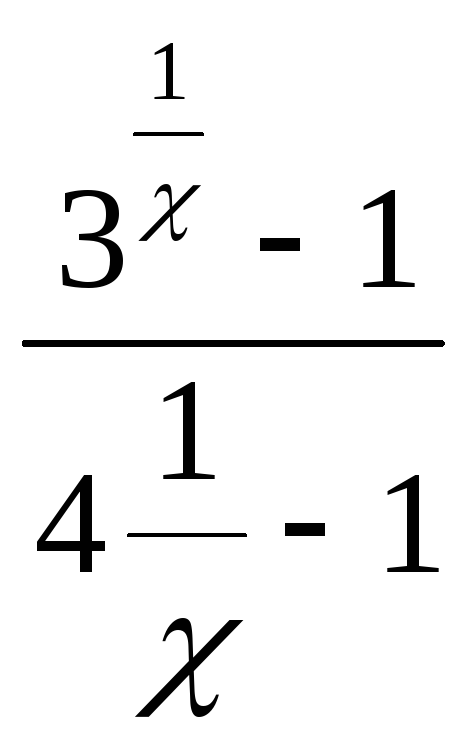 не существует, т.к.
у функции разные односторонние пределы.
не существует, т.к.
у функции разные односторонние пределы.
в)
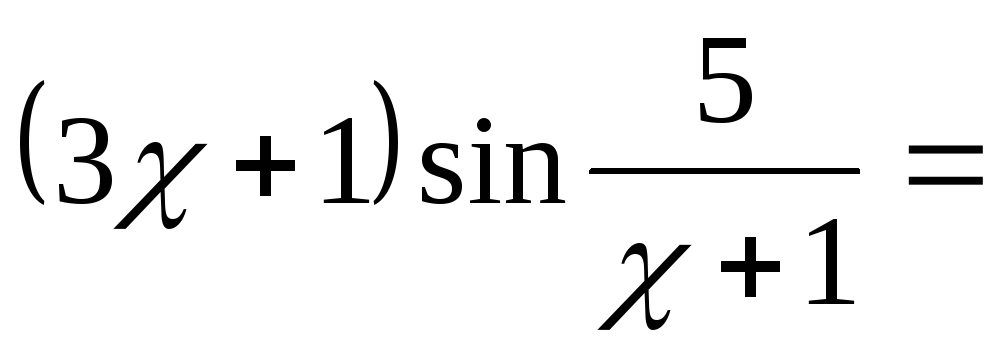
![]()
![]()
![]()
![]()
![]()
![]()
=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
г)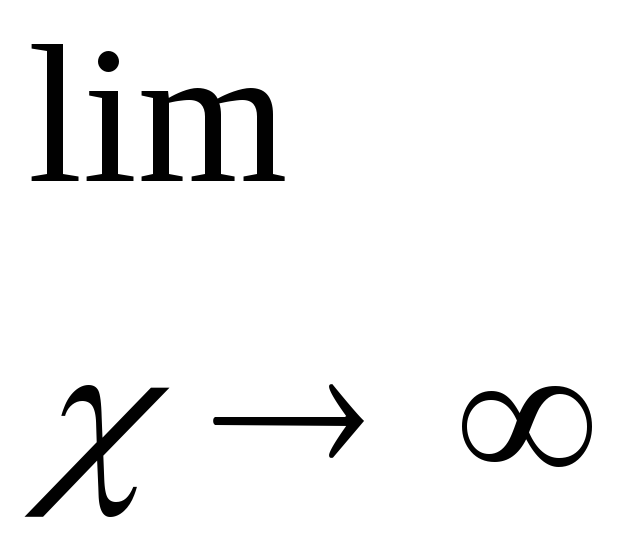
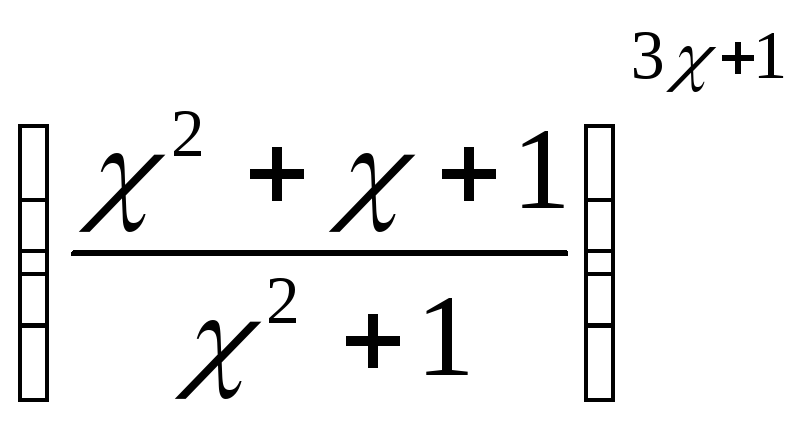
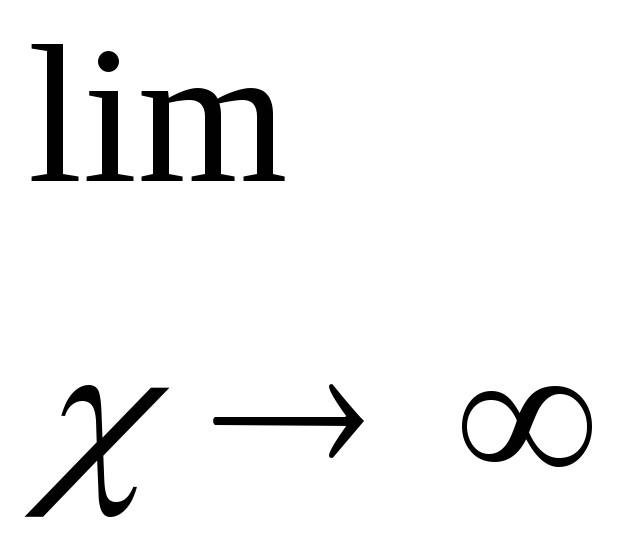

второй замечательный предел
![]()
![]()
![]()
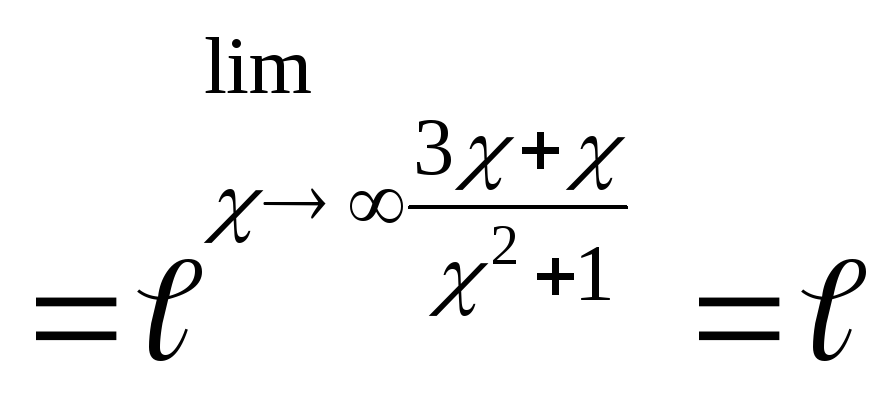
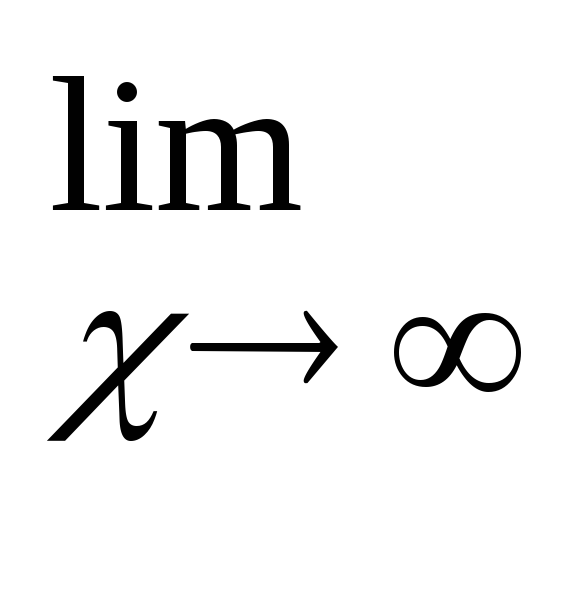

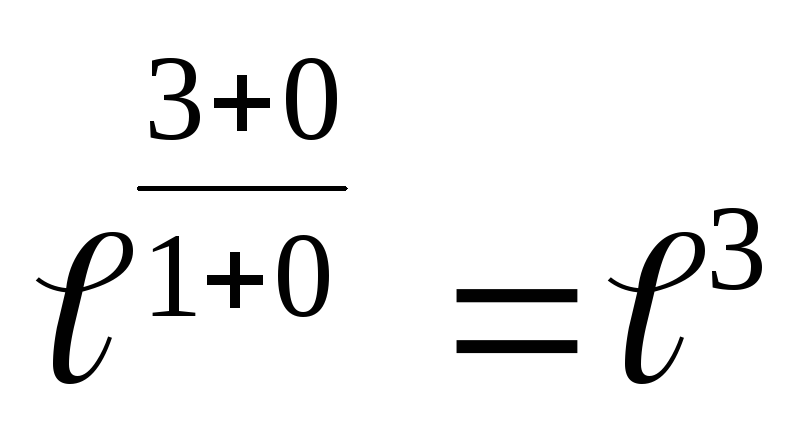 .
.
д)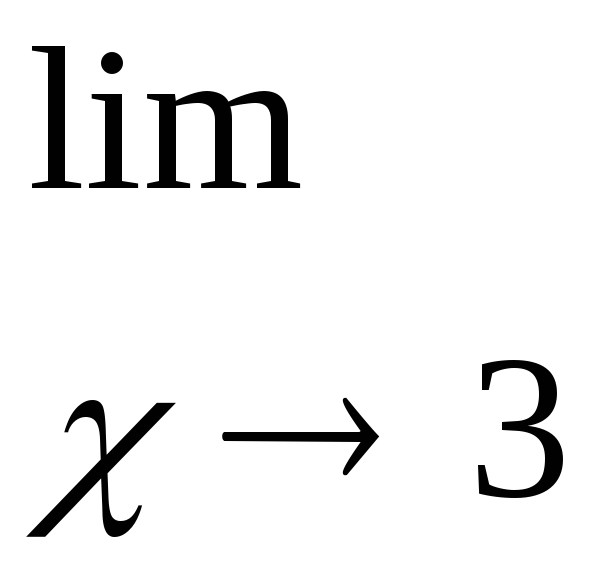
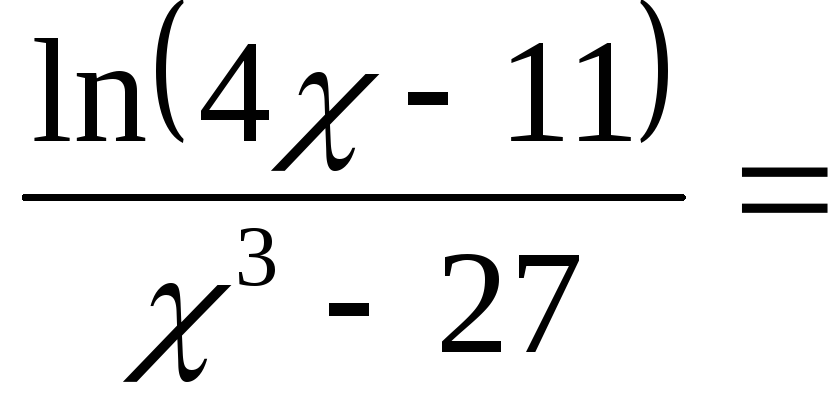
следствие второго замечательного предела:
=![]()
![]()
![]()
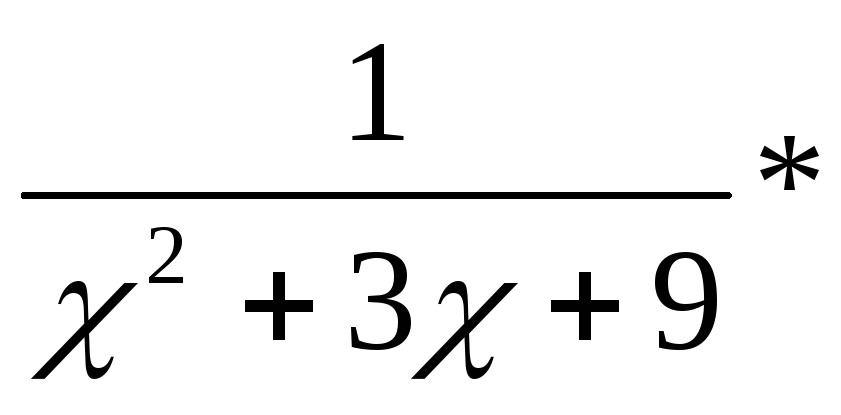
![]()
![]()
замена
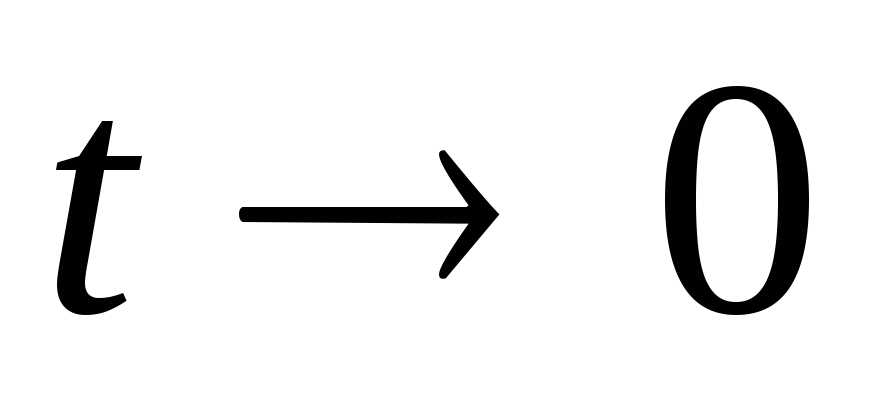
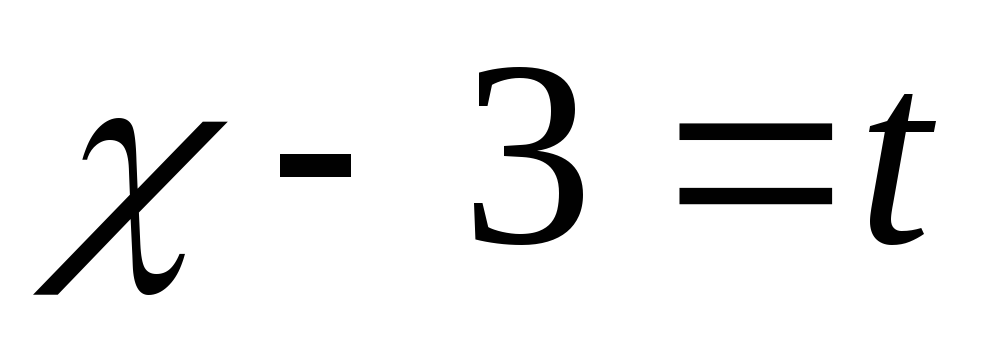 ;
;
 ;
;
 .
.
=![]()
![]()
![]() .
.
е)
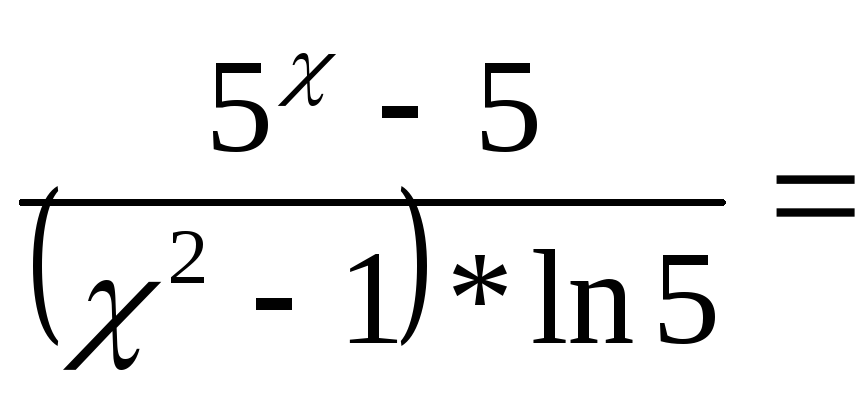
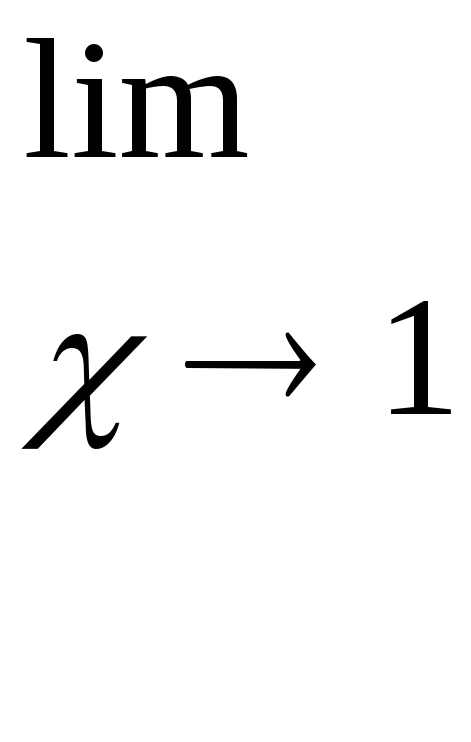

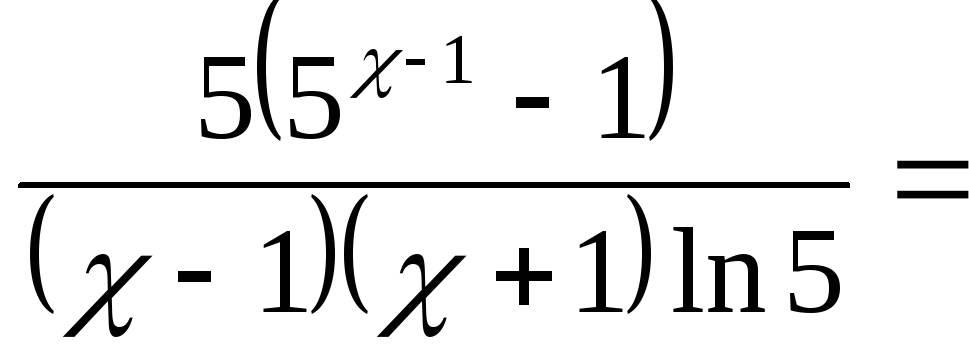
следствие второго замечательного предела:
=![]()
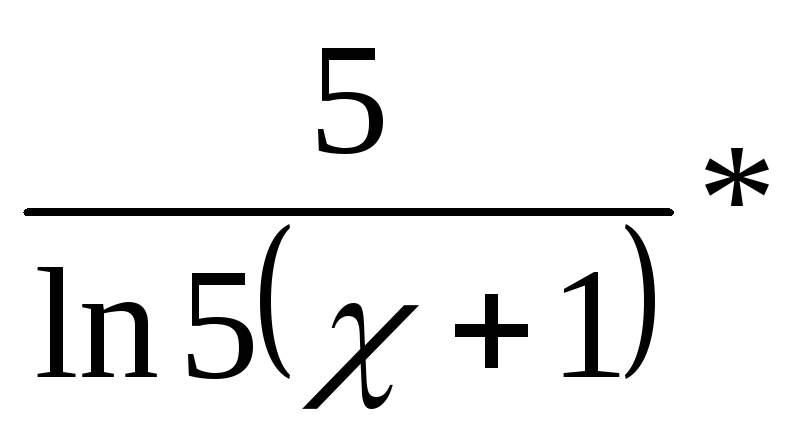
![]()
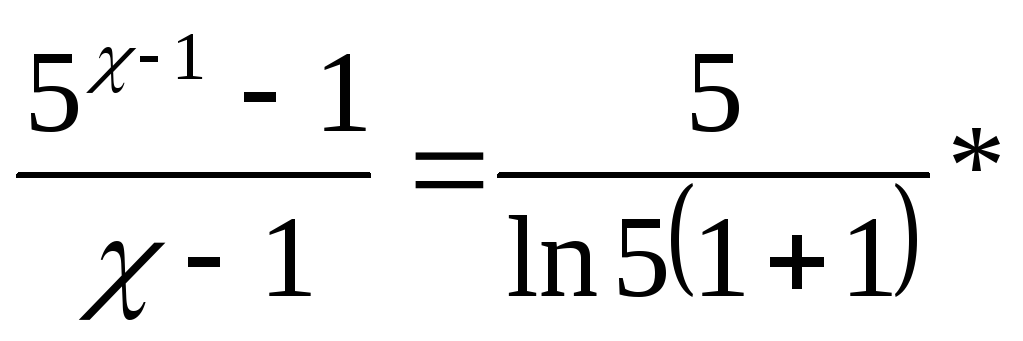
![]()
![]()
![]()
![]()
![]()
![]()
3.Выделите
главную часть вида
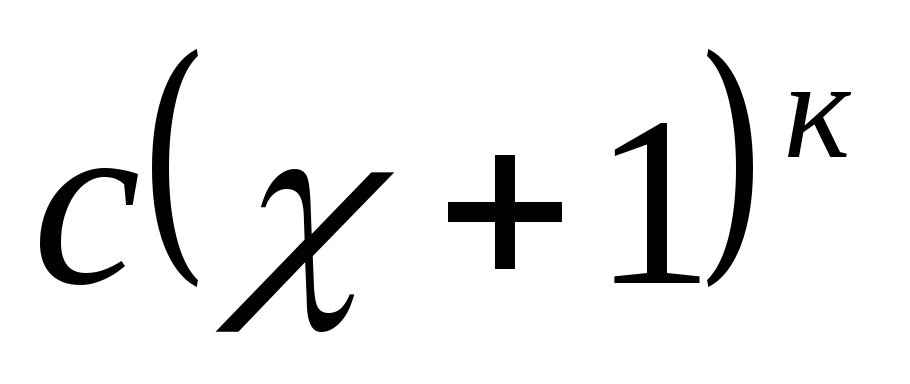 бесконечно малой
бесконечно малой
Найдём
при каких
 и
и
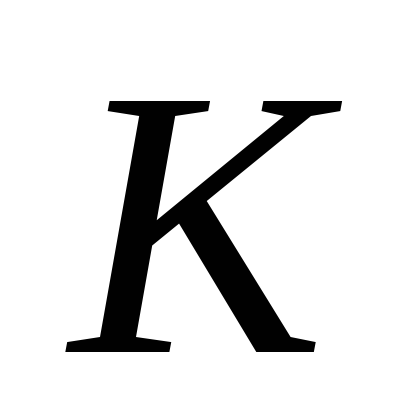
 будет
=1.
будет
=1.
![]()
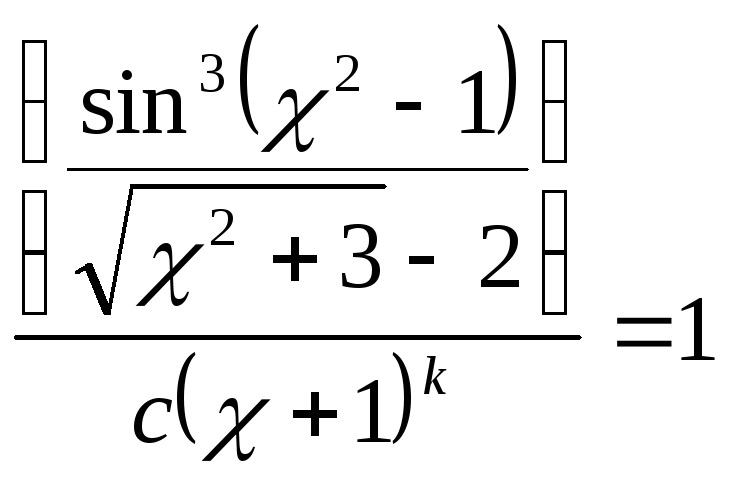
![]()
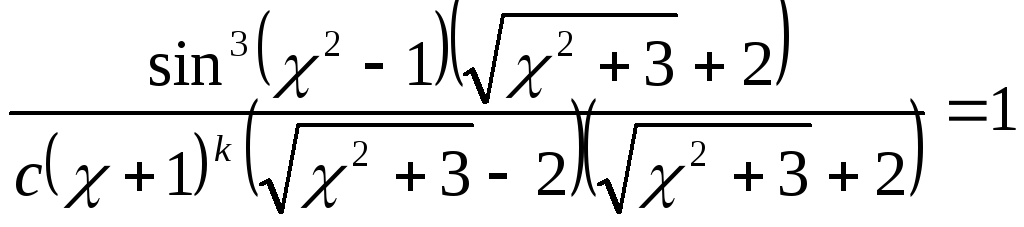
![]()
![]()
![]()
![]()
![]()
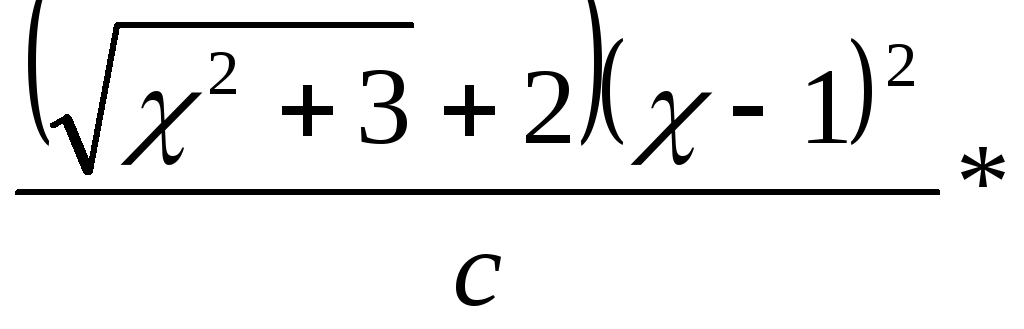
![]()
![]()
![]()
![]()
![]()
если
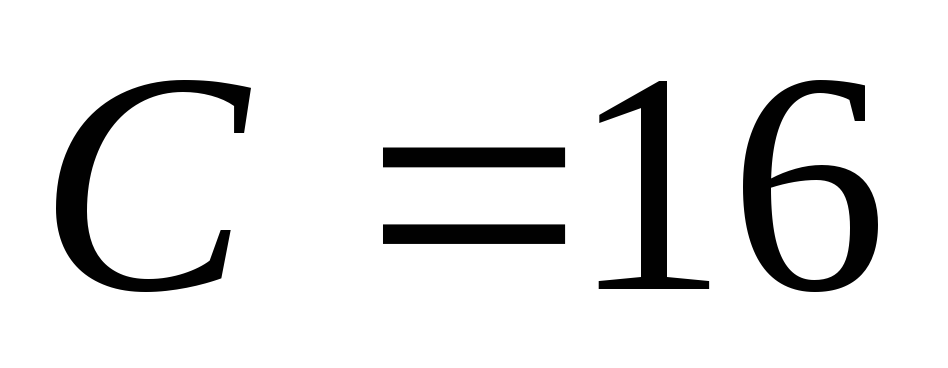 ,
,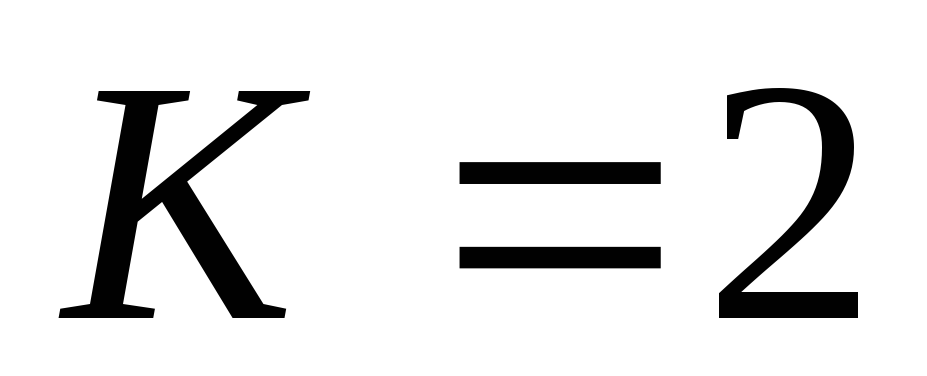 ,то
,то
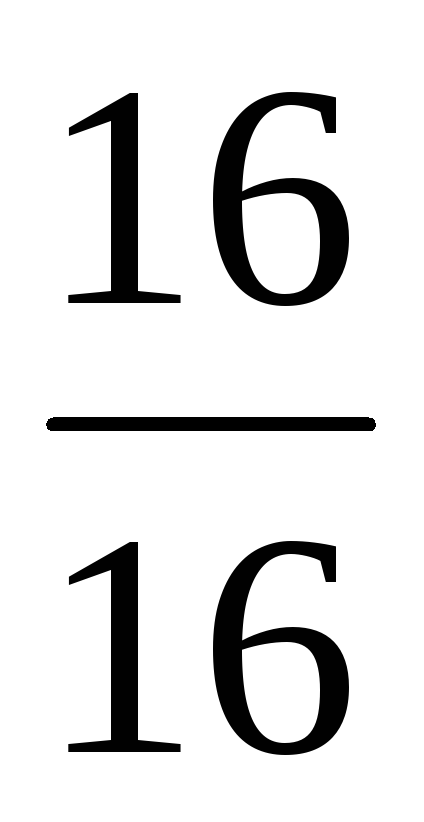

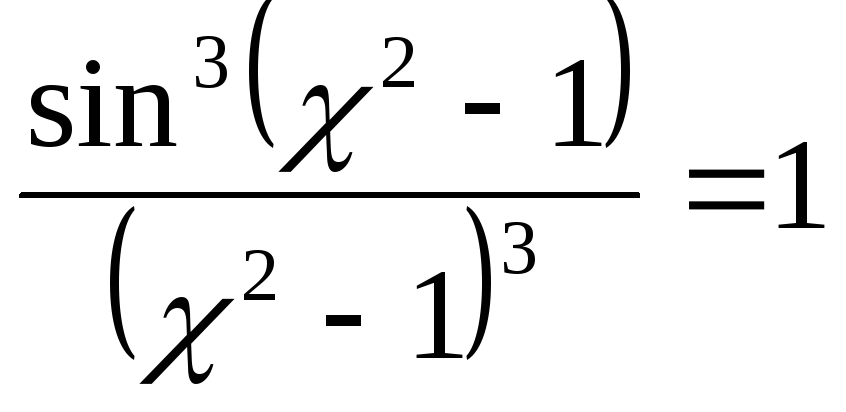
ответ: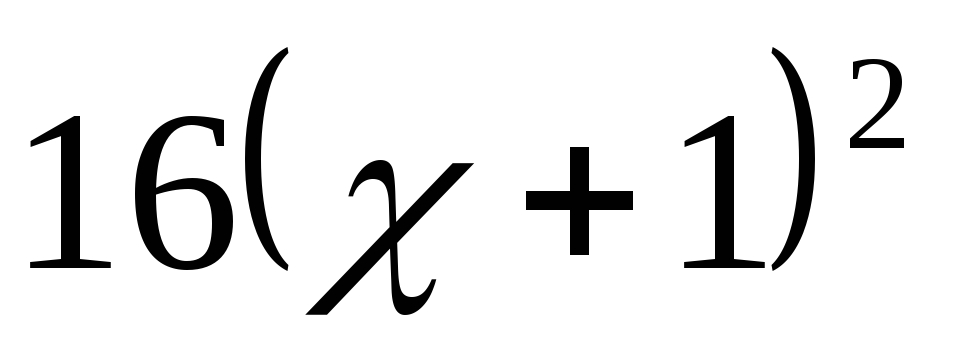 ,т.к.
,т.к.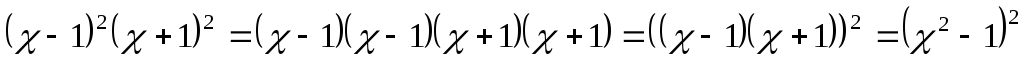
4.Найдите все точки разрыва и исследуйте их характер для функций:
а)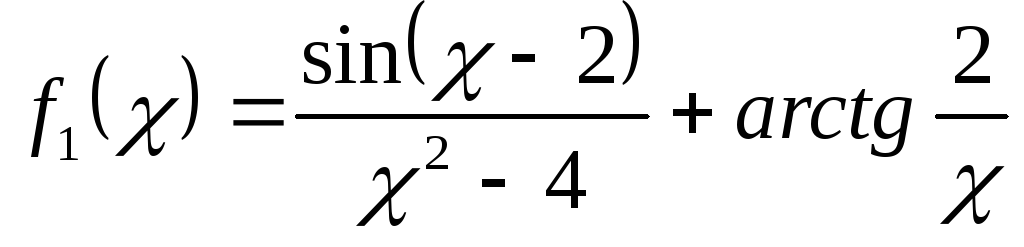
функция
не определена в точках
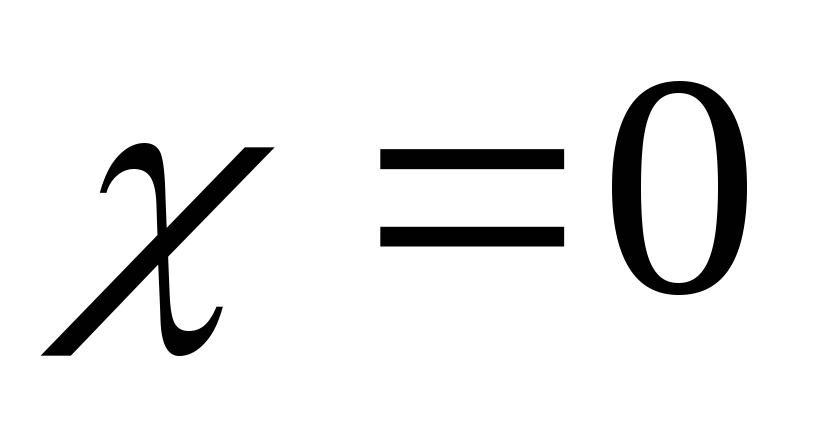 ,
,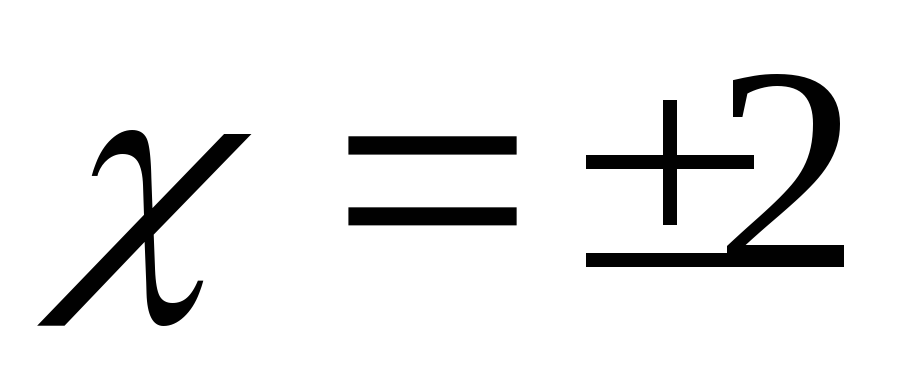
определим тип разрыва, найдем предел слева и справа.
х=0
Предел справа:
![]()
![]()
![]()
![]() ;
;
Предел слева:
![]()
![]() ;
;
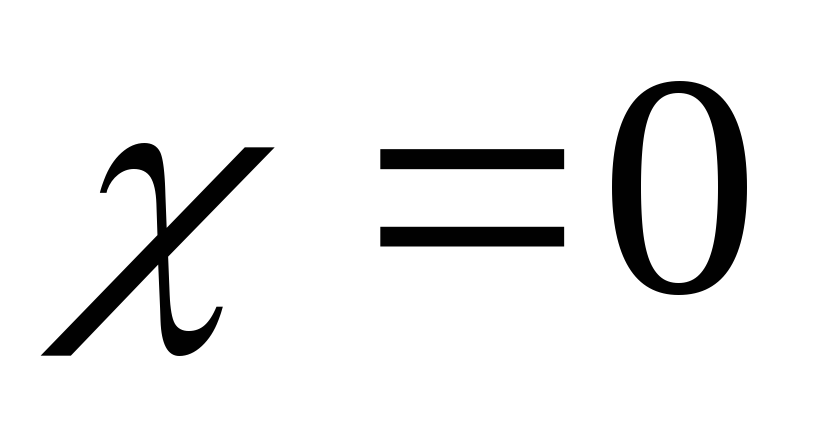 точка разрыва 1 рода.
точка разрыва 1 рода.
Исследуем
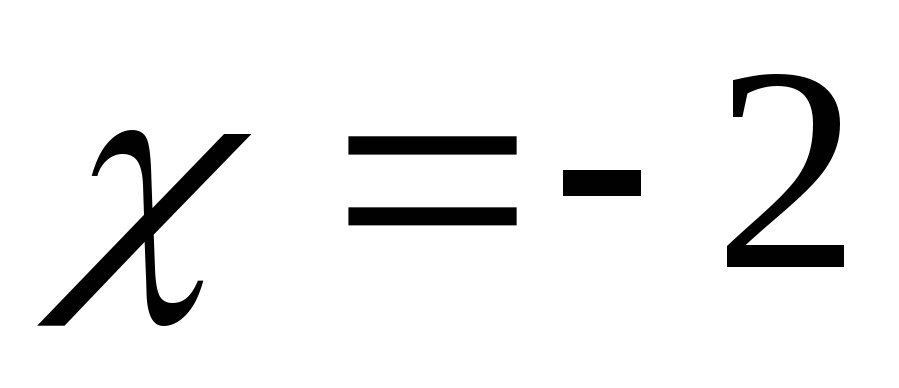
![]()
![]()
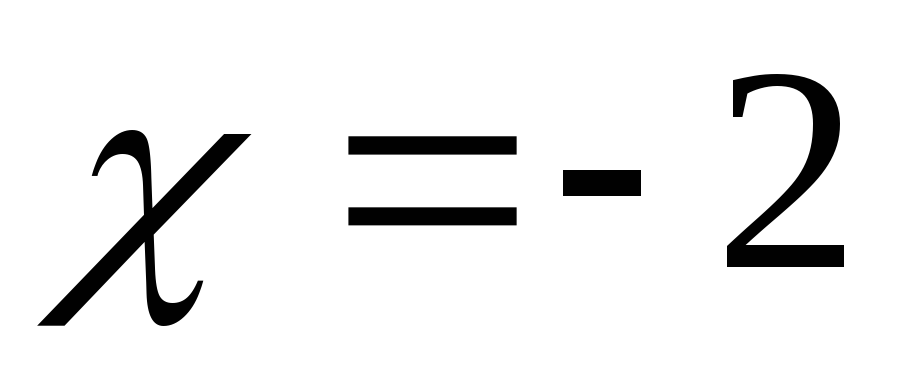 точка разрыва 2 рода.
точка разрыва 2 рода.
Х=2
![]()
![]()
![]()
![]() ;
;
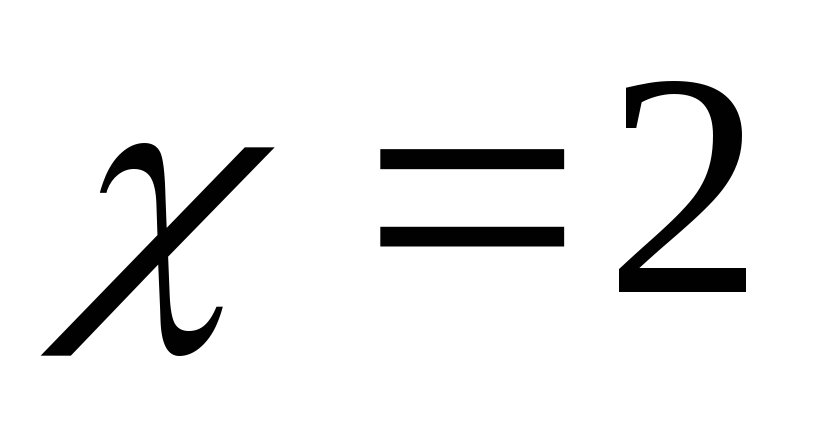 точка устранимого
разрыва.
точка устранимого
разрыва.
б)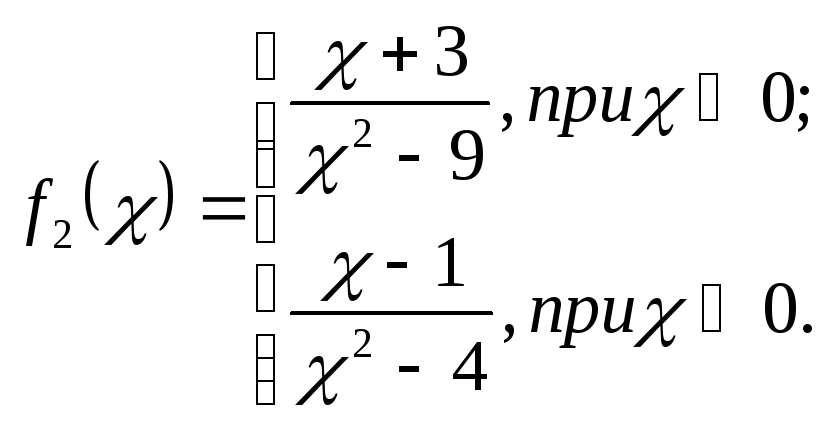 в точке
в точке
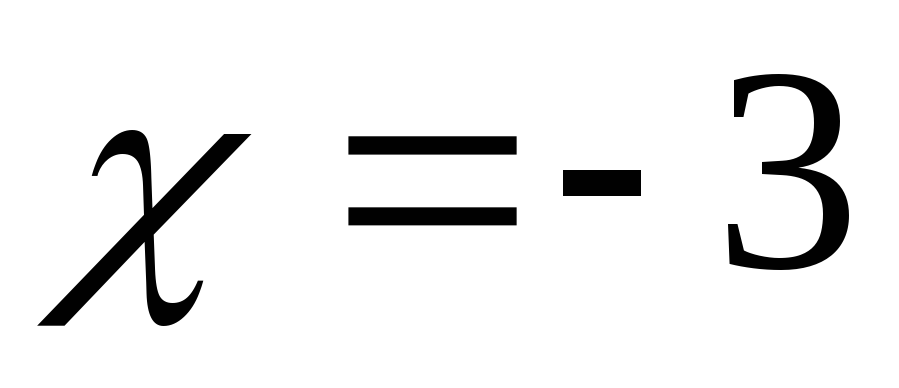
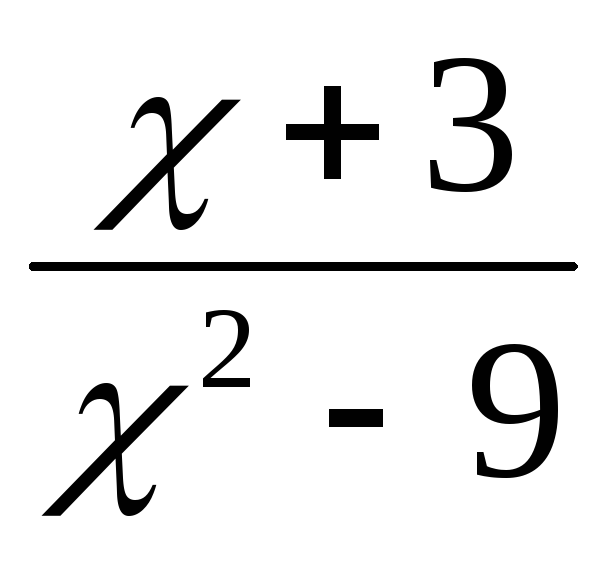 не определена
не определена
исследуем эту точку на характер разрыва:
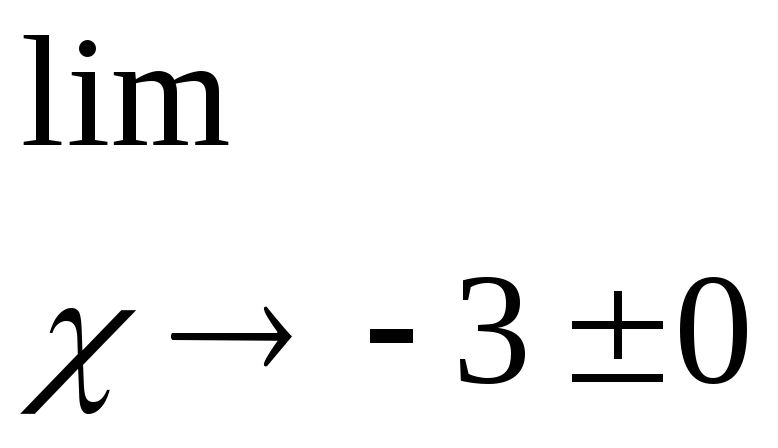
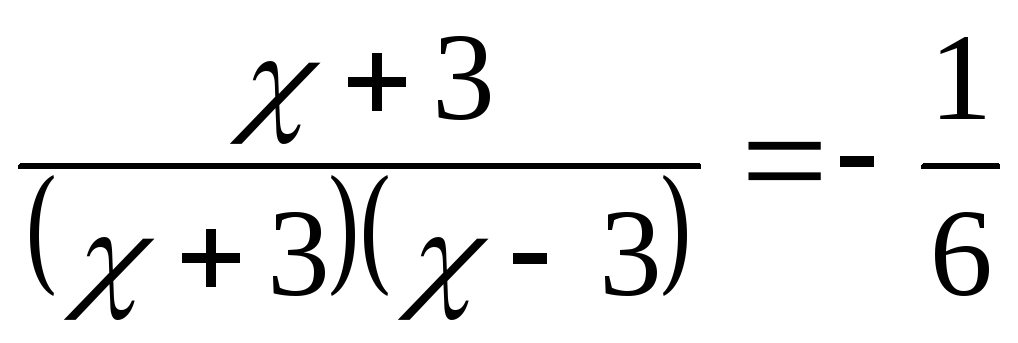 ;
;
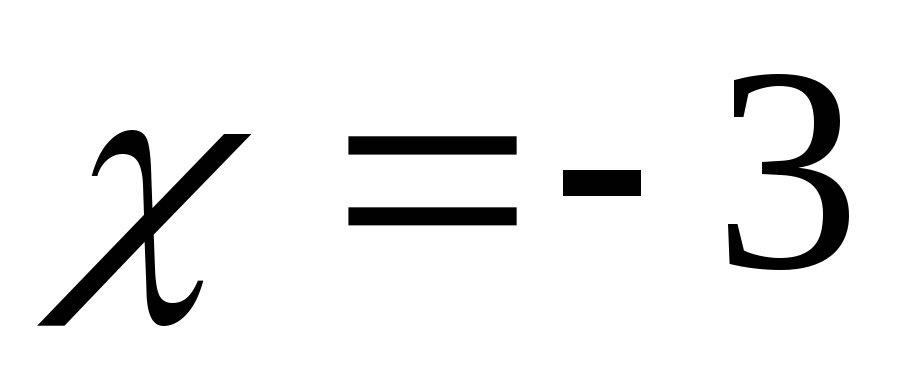 точка устранимого
разрыва
точка устранимого
разрыва
при
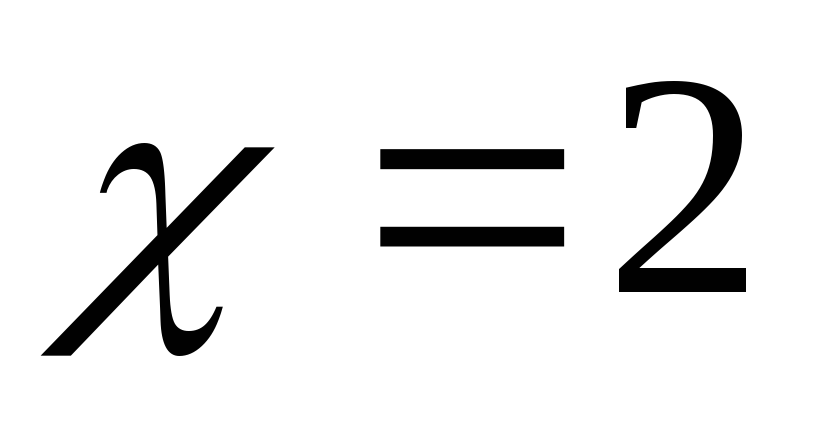
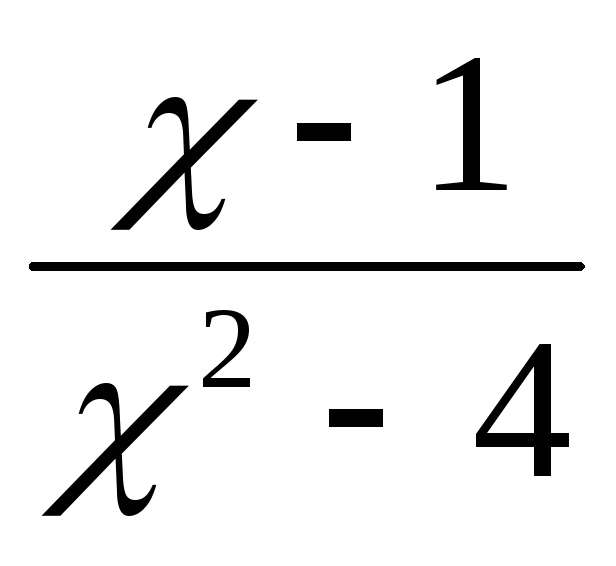 не определена.
не определена.

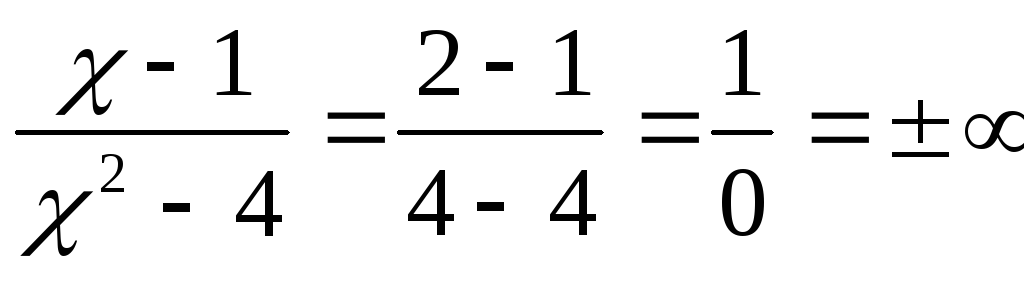 точка разрыва 2
рода.
точка разрыва 2
рода.
5.Найти производные от данных функций:
а)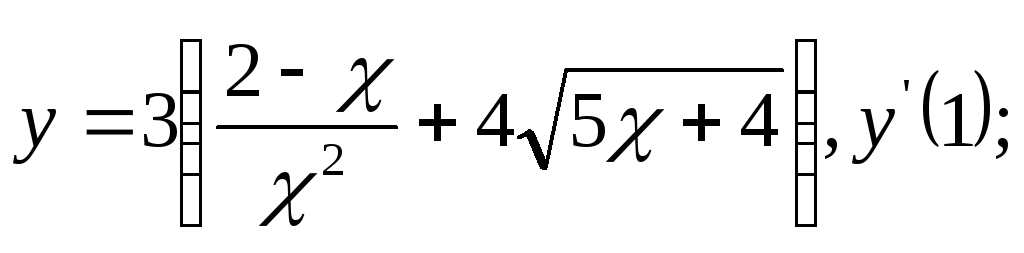
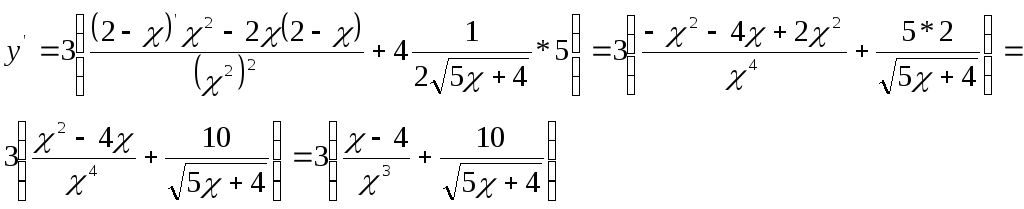
б)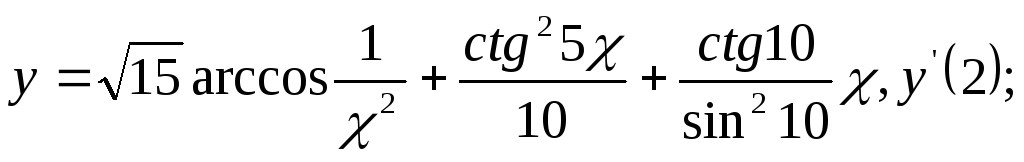
![]()
![]()
![]()
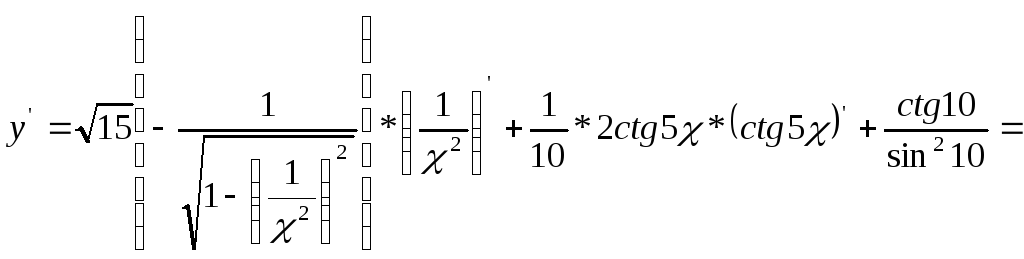
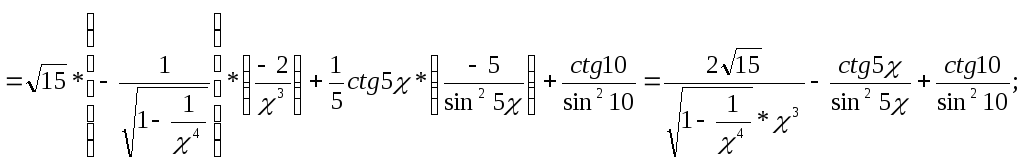
![]()
![]()
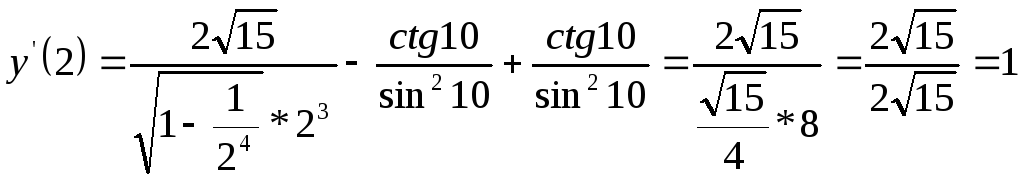 .
.
в)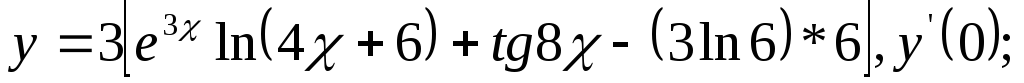
![]()
![]()
![]()
![]()
![]()
![]()
6.Дана
функция
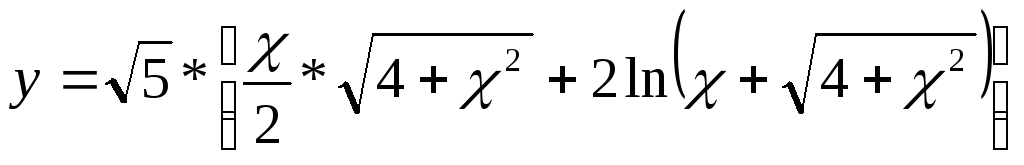 .
.
Найдите
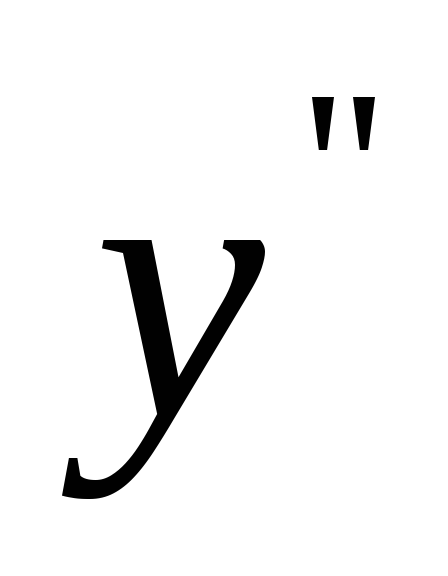 .
Вычислите
.
Вычислите
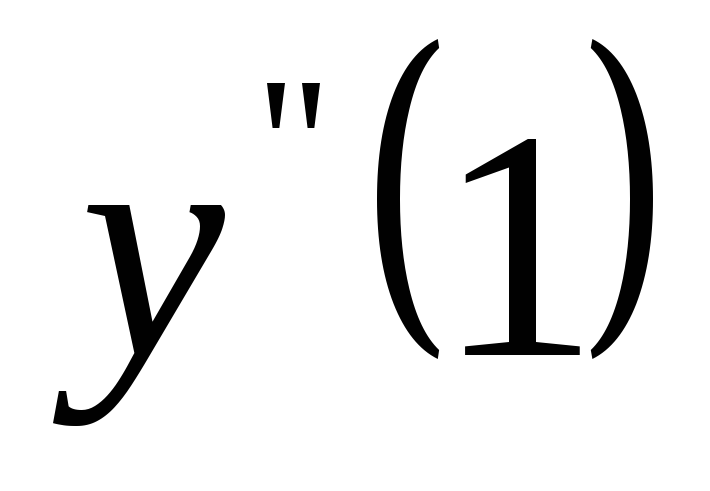 .
.
![]()
![]()
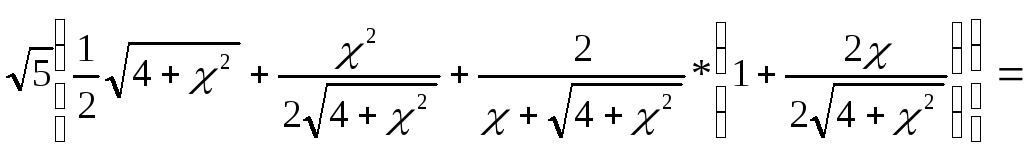
=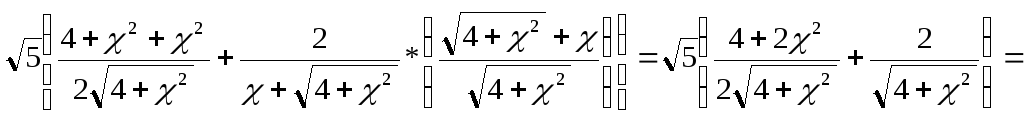
![]() ;
;
![]()
![]() .
.
7.Докажите,
что функция
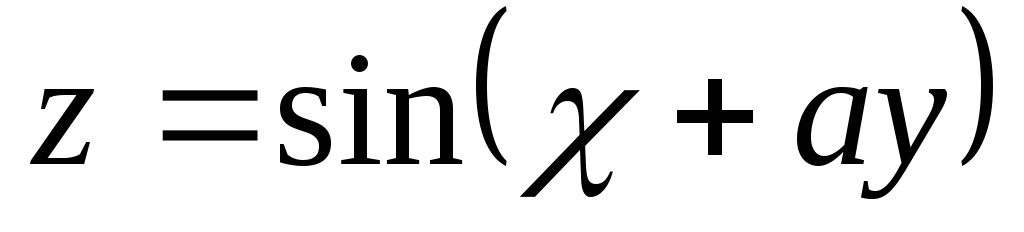 удовлетворяет уравнению
удовлетворяет уравнению
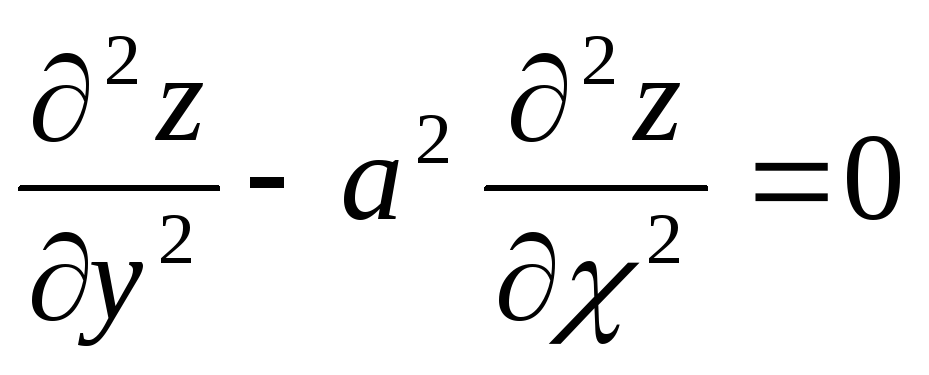 .
.
![]()
![]() ;
;
![]()
![]()
![]() .
.
8.Функция
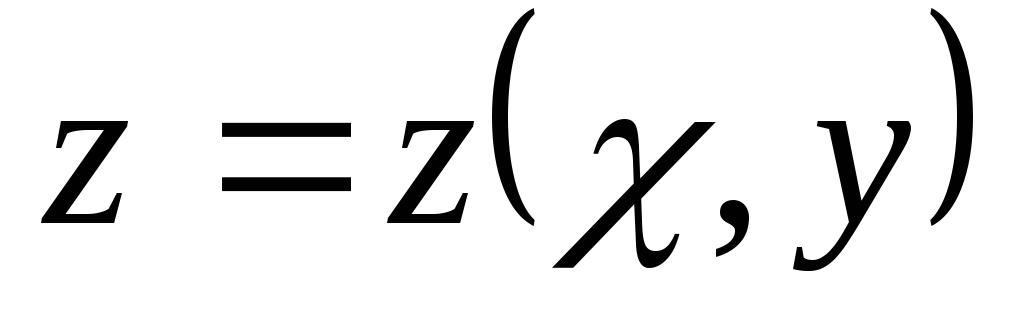 задана неявно уравнением:
задана неявно уравнением:
![]()
Вычислите:
а)
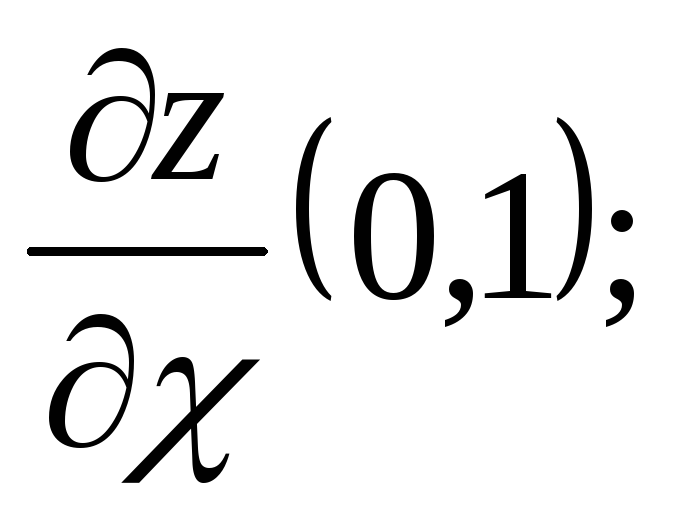 б)
б)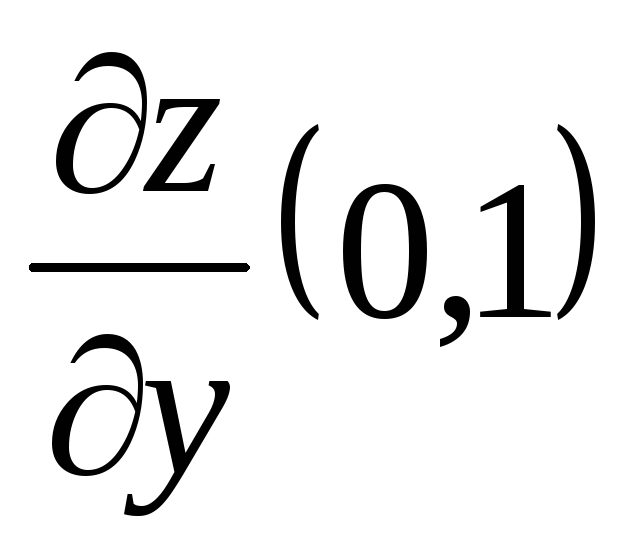 .
.
![]()
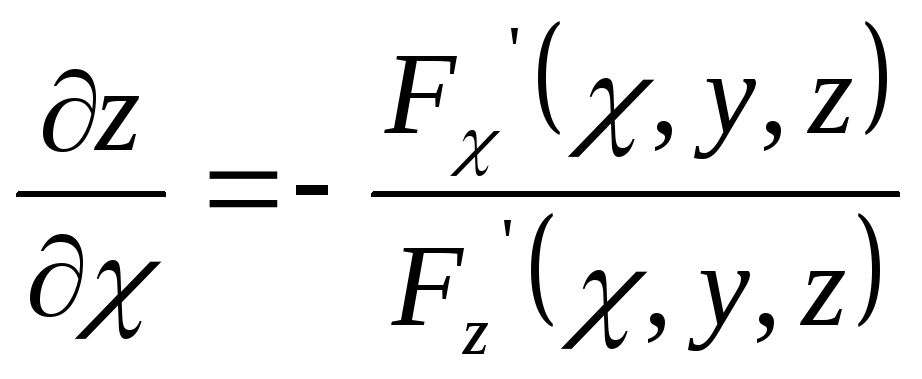
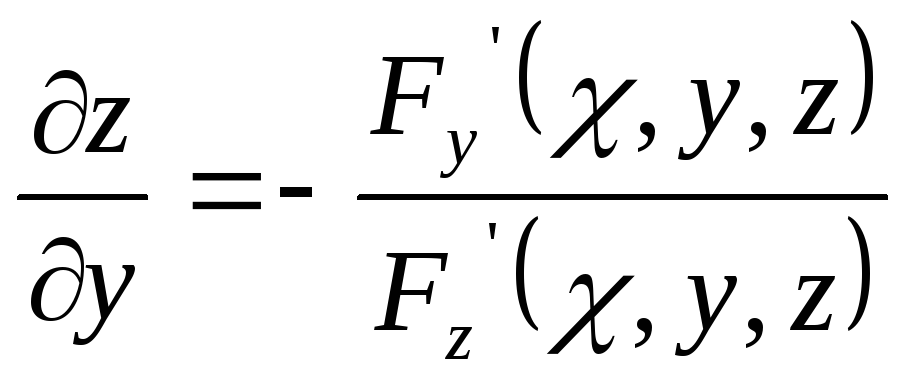
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;
![]()
![]() .
.
![]()
![]() .
.
9.Дана
функция
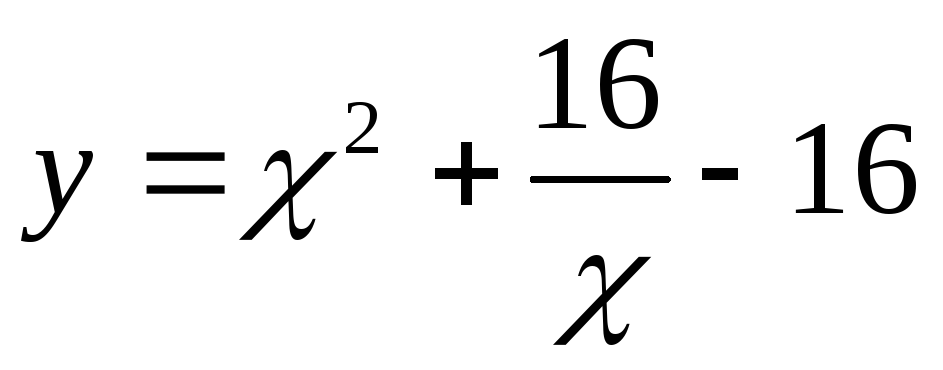 .
Найдите её наибольшее и наименьшее
значение на отрезке
.
Найдите её наибольшее и наименьшее
значение на отрезке
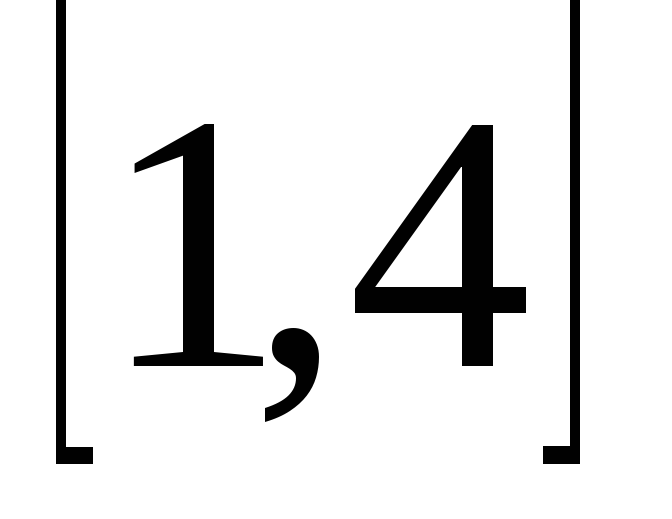 .
.
Функция принимает наибольшее, наименьшее значения либо в критических точках, либо на концах отрезка.
Найдем
критические точки:
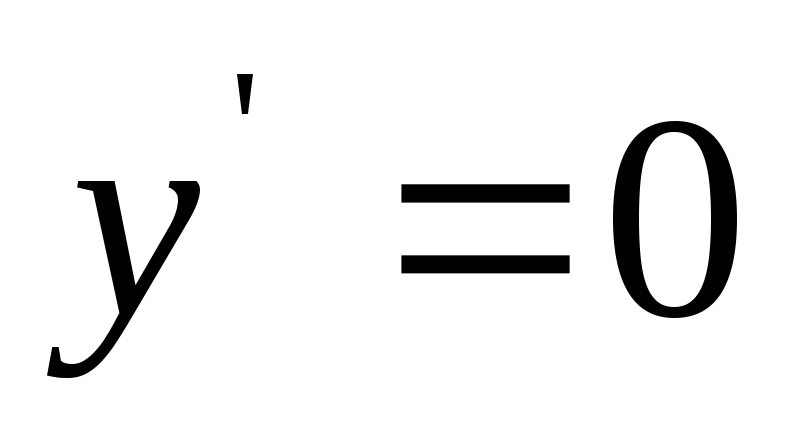
![]()
![]()
![]()
![]()
![]()
![]() критическая точка
критическая точка
Найдем
значение функции в критической точке
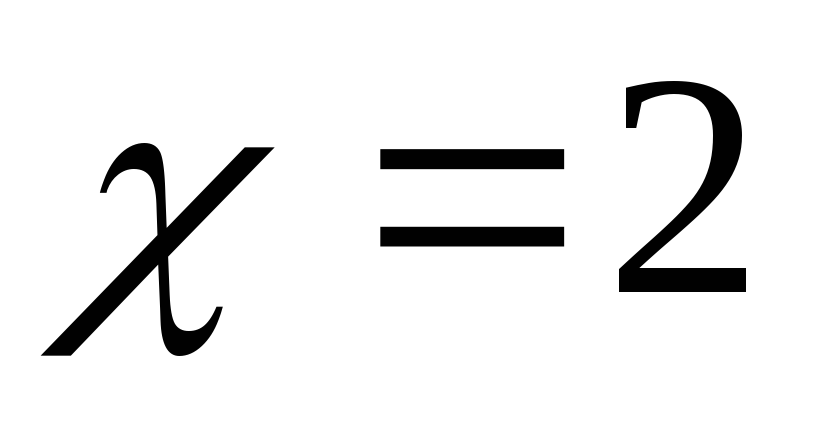 и на концах отрезка
и на концах отрезка
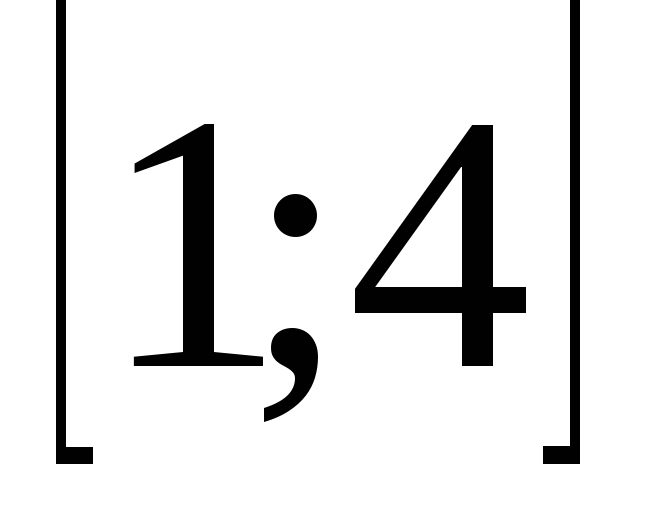
 наибольшее=4,
а
наибольшее=4,
а
 наименьшее=-4.
наименьшее=-4.
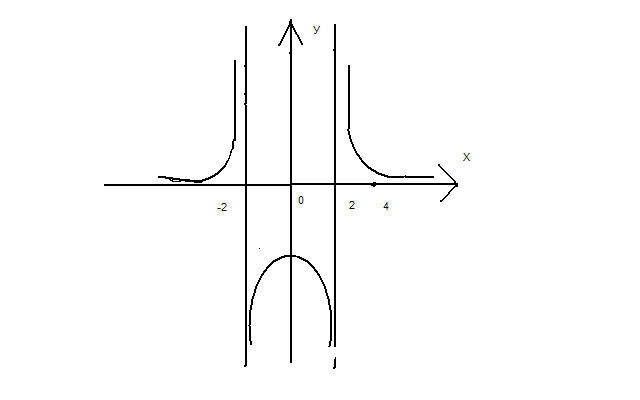
10.Проведите
полное исследование функции
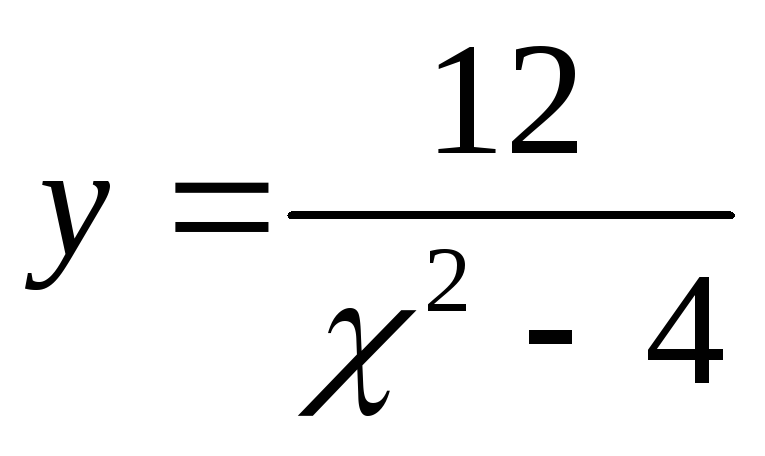 и постройте её график.
и постройте её график.
1)Область определения:
![]()
![]()
![]()
![]()
2)Решим вопрос о чётности
![]()
![]()
![]() функция
чётная, график симметричен относительно
оси
функция
чётная, график симметричен относительно
оси
![]() .
.
3)Исследуем на периодичность. Периодичности нет.
4)Точки пересечения с осями координат:
![]()
![]()
![]()
![]()
![]()
![]()
таких
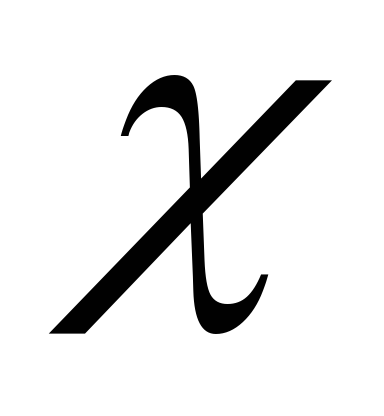 нет, с осью
нет, с осью
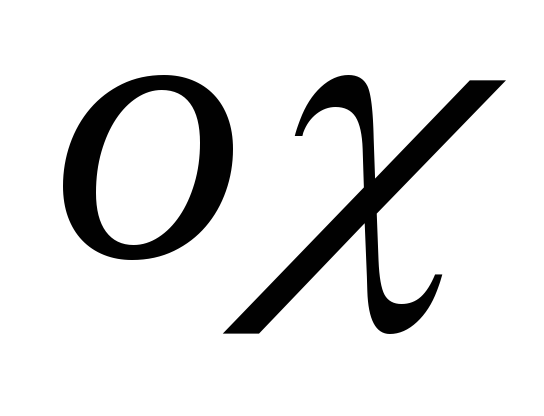 не пересекается
не пересекается
5)Точки
разрыва функции
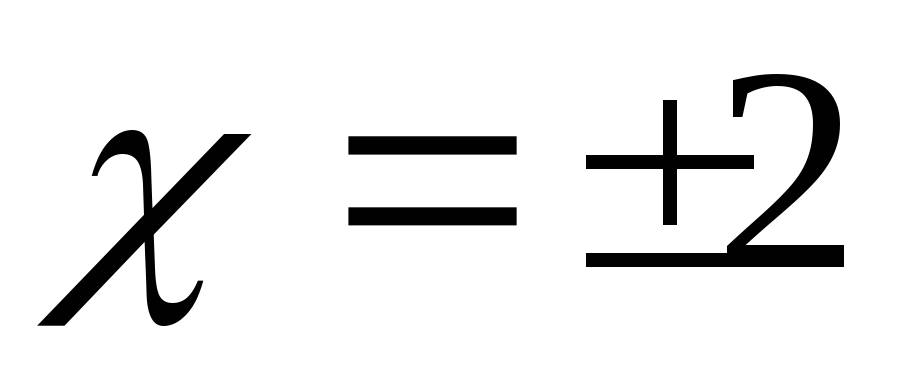
![]()
![]()
![]()
![]()
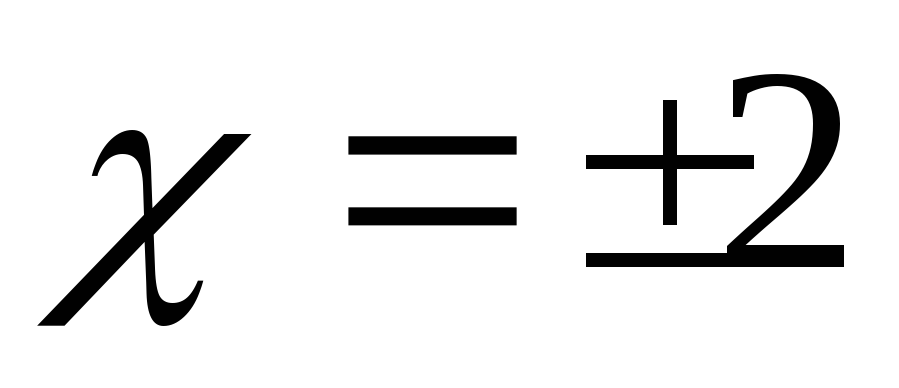 точка разрыва 2 рода.
точка разрыва 2 рода.
6)Проведем исследования на экстремум.
![]()
![]()
![]()
![]()
![]() .
.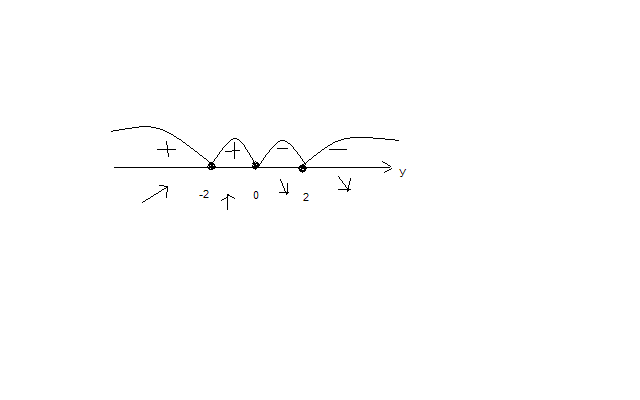
Определим знак производной в каждом интервале.
Функция
вырастает на
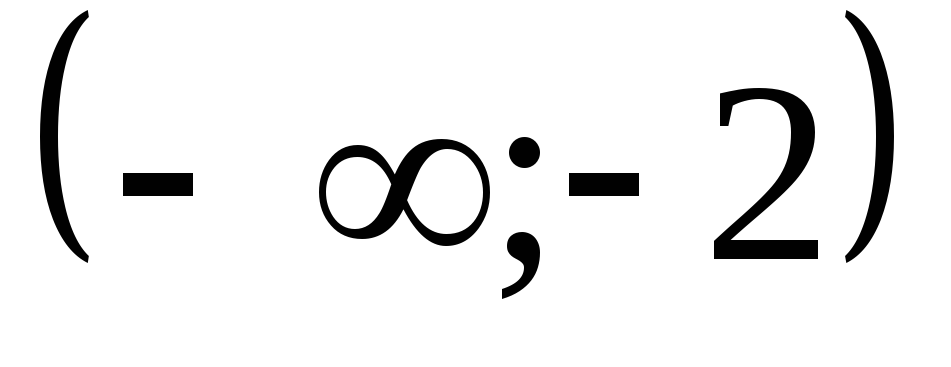 и
и
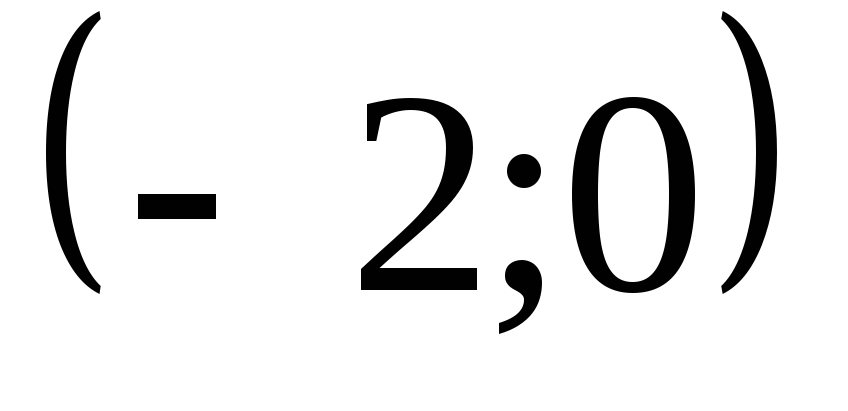 ,
,
Убывает
на
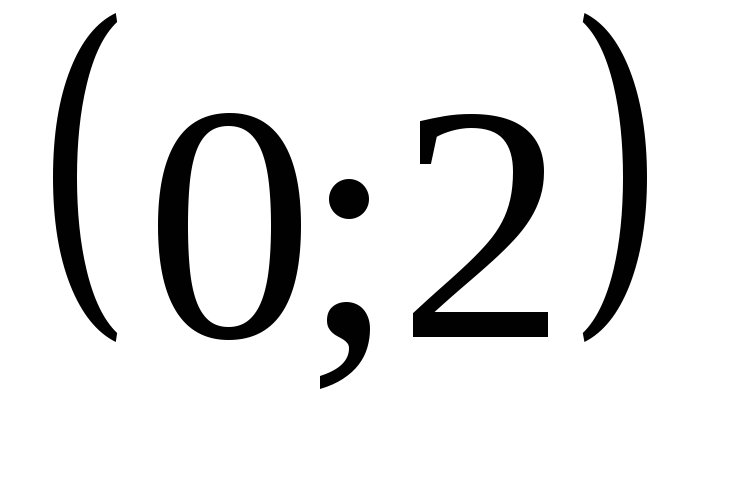 и
и
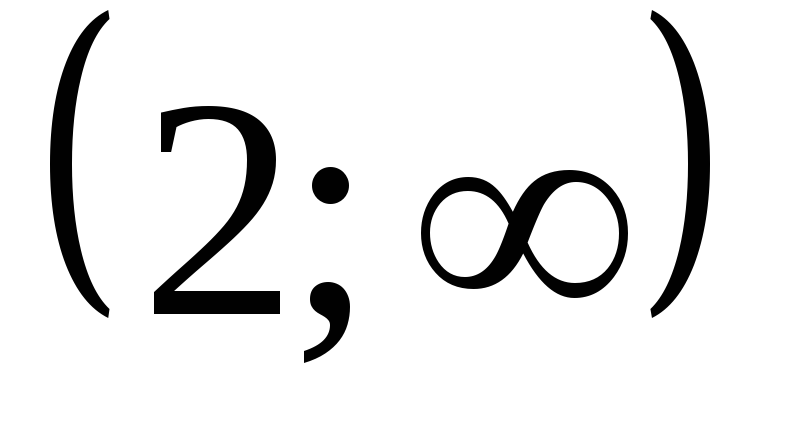 .
.
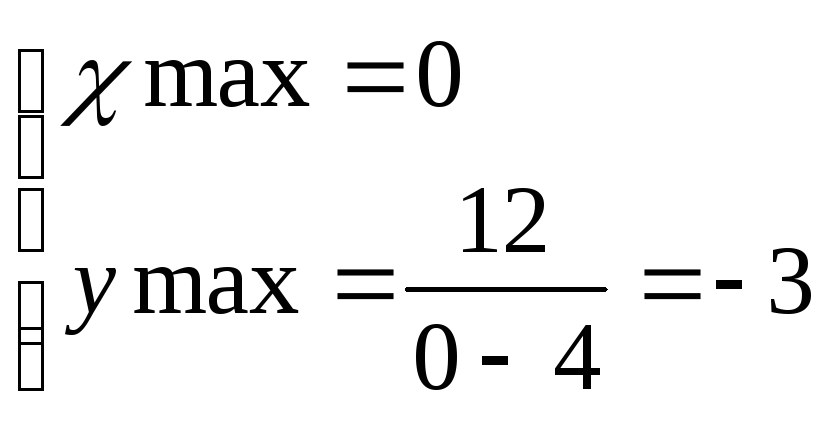
7)Найдем точки перегиба и интервалы выпуклости и вогнутости.
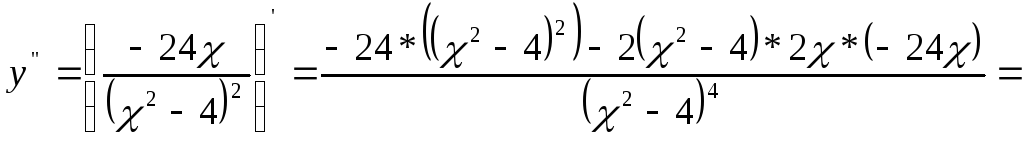
=![]() ;
;
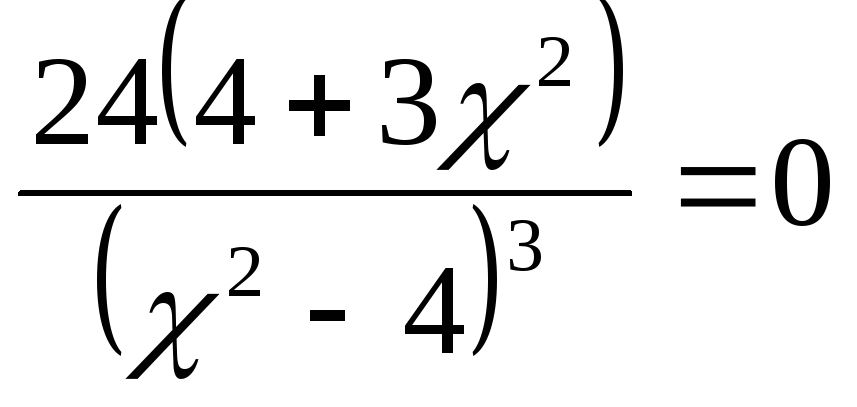
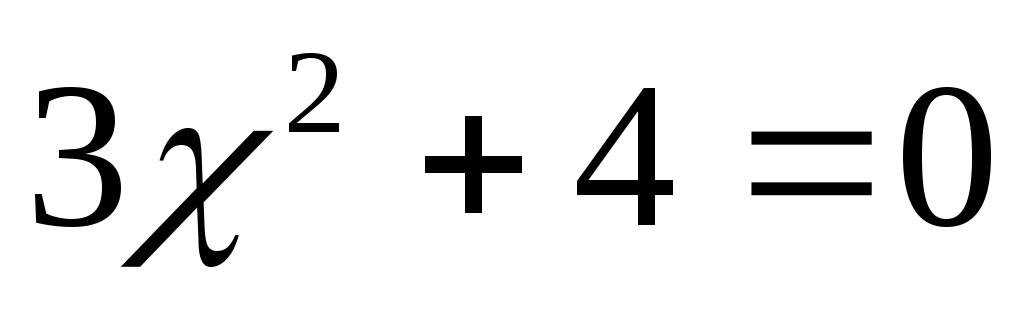
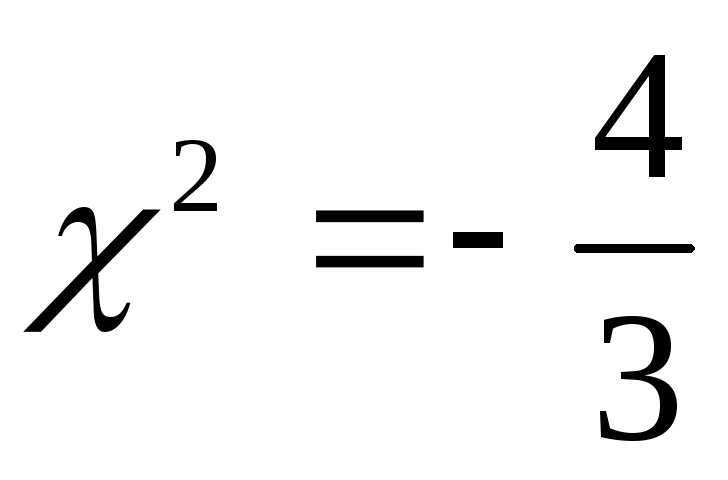 корней нет.
корней нет.
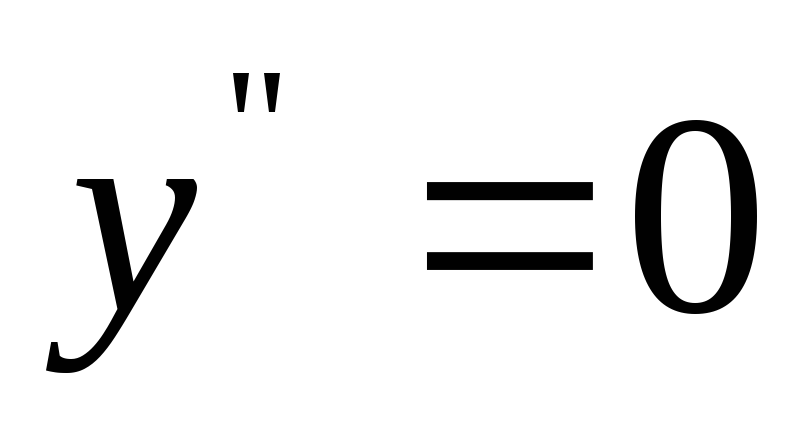 критических точек
нет.
критических точек
нет.
Исследуем область определения.
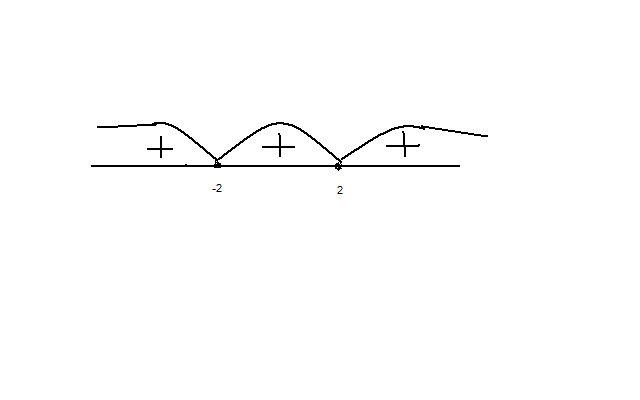
Выпуклый
на
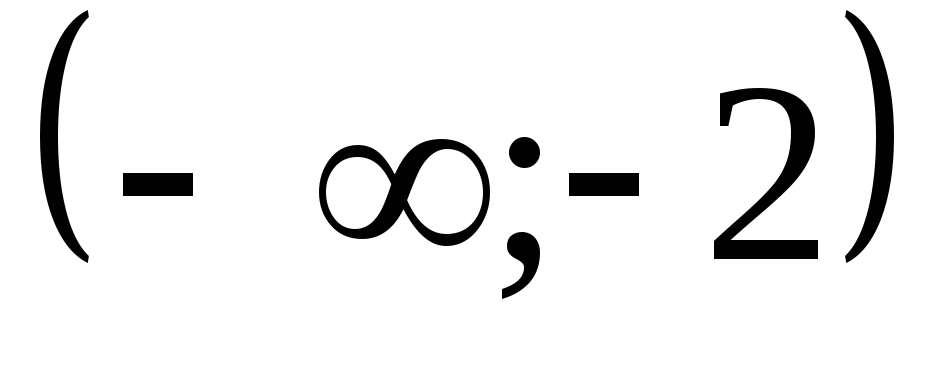 и
и
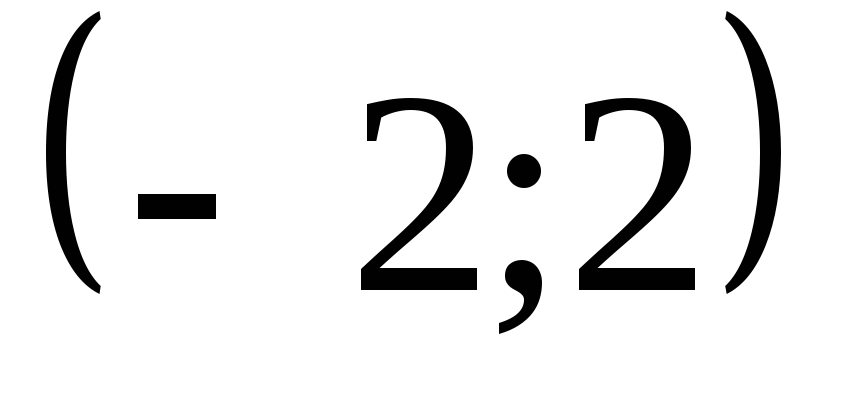 и
и
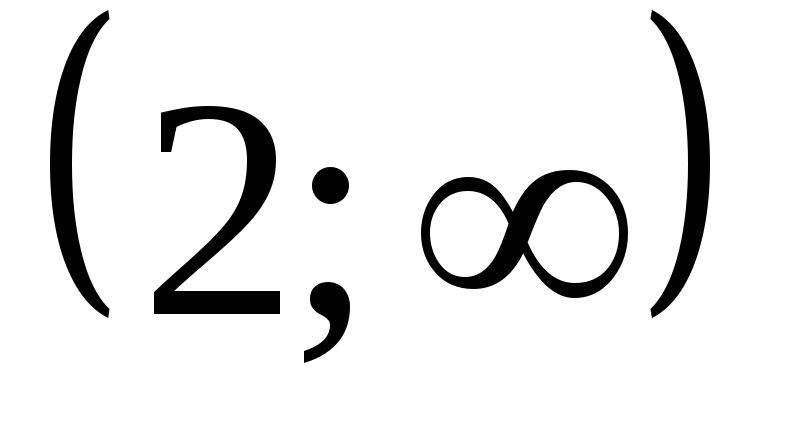 ,
точек перегиба нет.
,
точек перегиба нет.

![]()
![]()