Контрольная работа 2 / 2- 2_Высшая математика_2

МИНИСТЕРСТВО НАУКИ, ВЫСШЕЙ ШКОЛЫ И ТЕХНИЧЕСКОЙ ПОЛИТИКИ

ТОМСКИЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И

РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра высшей математики

УТВЕРЖДАЮ

Зав. кафедрой математики

М.Р.Куваев

высшая математика

КОНТРОЛЬНАЯ РАБОТА №_2

ВАРИАНТ_3.1

Название темы

2002

План:

1. Задание_1……………………………………….3

2. Задание_2……………………………………….3

3. Задание_3……………………………………….3

4. Задание_4……………………………………….3

5. Задание_5……………………………………….3

6. Задание_6……………………………………….3

7. Задание_7……………………………………….3

8. Задание_8……………………………………….4

9. Задание_9……………………………………….4

10. Задание_10……………………………………...4

11. Список литературы…………………………...6

Путь нахождения искомого варианта:

V=N*k*div100,

где N – количество вариантов;

k – две последние цифры пароля;

div – целочисленное деление.

V=17*10*div100=170div100=1

1. f(x) = x – 4 + 8 – x ;

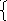
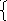x – 4  0; _ x  4;

8 – x  0; y  8;

x  [4;8] – область определения функции.

2. f(x) = 1 + x _, f[f(x)];

1 – x _{1 +} 1 + x 1 – x + 1 + x

f[f(x)] = 1 + f(x) ₌ 1 – x ₌ 1 – x ₌ 2 _{= -} 1 ;

1 – f(x) _{1 -} 1 + x 1 – x – 1 – x -2x x

1 – x 1 – x

2*f(f(2)) = -2/2 = -1.

1 5

3. lim 6n⁴ – n + 5 ₌ 6 – n³ + n⁴ ₌ 6 ₌ 3.

n 3n⁴ + 5n – 1 5 _- 1 2

2 + n³ n⁴

______

4. lim (n⁴ + 2n – n²)*n² : До множим числитель и знаменатель на сопряжённое

n 3n + 4 знаменателя:

lim (n⁴ + 2n – n⁴)*n² ₌ lim ______2n³_________ ₌

n (3n + 4)(n⁴ + 2n + n²) n n³(3 + 4/n)(1 + 2/n³ + 1)

₌ lim _______2__________ ₌ _2_ ₌ 1/3.

n (3 + 4/n)(1 + 2/n³ + 1) 3*2

5. lim (3x + 1)sin 5 ₌ sin 5  5 ₌ lim 5(3x + 1) ₌ lim 15 + 5/x ₌ 15.

x x + 1 x+1 x+1 x x + 1 x 1 + 1/x

6. lim 3^1/x – 1 ₌ lim (3/4)^1/x – 1/4^x ₌ 0 ₌ 0.

x 4^1/x – 1 x 1 – 1/4^x 1

((x²+1)/x)*(x*(3x+1)/x²+1))

7. lim x² + x + 1 ^{3x+ 1}₌ lim _{1 +} x ^3x+1₌ lim _{1 +} x

x x² + 1 x x² + 1 x x² + 1 =

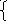
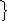
= exp lim 3x² +x

x x² + 1 = exp³ = e³.

x – 1 = t

8. lim 5^x – 5 ₌ x = 1 + t ₌ lim 5^1+t – 5 ₌ lim 5(5^t - 1) ₌

x (x² – 1)ln5 x + 1 = t + 2 t0 t(t + 2)ln5 t0 t(t + 2)ln

₌ 5^t – 1  ln5 ₌ lim 5tln5 ₌ lim 5 ₌ 5 ₌ 2,5.

t0 t0 t(t + 2)ln5 t0 t + 2 2

9.

a(x) ₌ sin³(x² – 1) , x  -1;

x² + 3 – 2

sin³(x² – 1)  (x² – 1)³, x  -1; a(x) ₌ (x² – 1)³(x² + 3 + 2) ₌

x² + 3 – 4

= (x² – 1)²(x² + 3 + 2) = (x – 1)²(x + 1)²(x² + 3 + 2) = (-1 –1)²(x + 1)²(2 + 2) =

= 8(x + 1)².

10. a) f₁(x) ₌ sin(x – 2) ₊ arctg2/x, точки x = 0, x =  2 – точки подозрительные на разрыв.

x² – 4

Определим односторонние пределы в точках :

lim sin(x – 2) ₊ arctg2/x ₌ sin(-2) ₊ arctg(-) ₌ sin2 -  _;

x0-0 x² – 4 -4 4 2

lim sin(x – 2) ₊ arctg2/x ₌ sin2 ₊  _ x = 0 – точка разрыва -рода, «скачёк».

x0+0 x² – 4 4 2

f₁(x) ₌ sin(x – 2) ₊ arctg2/x ₌ sin(-4) ₊ arctg2/(-2 – 0) ₌

x² – 4 (-2 – 0 – 2)(-2 – 0 + 2)

₌ sin4 _-  ₌ -;

-4(-0) 4

lim sin(x – 2 ) ₊ arctg2/x ₌ sin(-4) ₊ arctg(-1) ₌ + _

x-2-0 (x – 2)(x + 2) -4(+ 0)

_ x = -2 – точка разрыва 2- рода (бесконечный разрыв);

lim sin( x – 2 ) ₌ sin(x – 2)  (x – 2) ₌ lim 1 ₊ arctg2/x ₌

x20 (x - 2)(x + 2) x20 x20 x + 2

= 1/4 + /4  в точке x = 2 – устранимый разрыв.

б) f₂(x) ₌ x + 3 при x<0 ; x = -3, x = 0, x = 2 – точки подозрительные

x² + 9 на разрыв;

x – 1 при x>0

x² – 4

lim x + 3 ₌ lim 1 ₌ 1/6  в точке x = -3 устранимый разрыв;

x-30 (x – 3)(x + 3) x-30 x – 3

lim x + 3 _{= _} 1

x0-0 (x² – 9) 3  в точке x = 0 разрыв 1-рода(«скачёк»);

lim x – 1 ₌ 1

x0+0 (x² – 4) 4

lim x – 1 ₌ 1 ₌ -

x2-0 (x – 2)(x + 2) (-0)4

lim x – 1 ₌ 1 ₌ +  в точке x = 2 разрыв 2-рода(бесконечный раз

x2+0 (x – 2)(x + 2) (+0)4 разрыв) .

Список литературы:

1. Шыпаев В.С. Начала высшей математики: Пособие для вузов. – М.: Дрофа, 2002.

2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. – М.: Наука. 1984.

3. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Физматгиз, 1963.

6