Контрольная работа 2 / 2- 4_Высшая математика_5
.doc
Министерство образования РФ
Томский государственный университет
систем управления и радиоэлектроники (ТУСУР)
ТМЦ ДО
Контрольная работа №2
по дисциплине «Высшая математика-1»
авторы: Л. И. Магазинников
А. Л. Магазинникова
V= (10*45) div 100=4
Выполнил:
студент ТМЦДО
специальности
№1. (781.РП). Составьте общее уравнение прямой, если точка P(2,5) служит основанием перпендикуляра, опущенного из начала координат на эту прямую.
Решение:
M(0,0) P(2,5).
Искомая прямая ортогональна вектору MP(2, 5).
Теперь по правилу 2 находим искомое уравнение: 2х+5у-(2*2+5*5)=2х+5у-29=0.
Ответ: 2х+5у-29=0.
№2 (882.БЛ). Запишите общее уравнение прямой, параллельной прямой 4х+2у+5=0 и отсекающей от первого координатного угла треугольник площадью 9 кв. ед.
Решение:
Из параллельности прямых следует
равенство их векторов – нормалей N(4,2).
Найду уравнение прямой в виде у=кх+b т.
к.
![]() ,
и
,
и
![]() ,
и площадь треугольника отсекаемого
искомой прямой равна S=
,
и площадь треугольника отсекаемого
искомой прямой равна S=![]() .
По условию задачи S=9 имею уравнение:
.
По условию задачи S=9 имею уравнение:
S=![]() ,
,
![]() ,
,
C=![]() 12.
12.
Искомое уравнение прямой равно у=-2х+6, отсюда у+2х-6=0.
Ответ: у+2х-6=0.
№3.(5А3.РП). Запишите общее уравнение плоскости, проходящей через точку М(4, -1, 3) параллельно оси ОХ и перпендикулярной к плоскости х-3у+4z-5=0.
Чтобы найти уравнение плоскости нужно найти вектор нормали и точку лежащую на плоскости. Так как плоскость параллельна ОХ т. е. вектору М0(1, 0, 0) и по условию направляющим для нее будет вектор М1(1, -3, 4).
Значит вектор нормали равен М0М1(0, 4, 3).
Составлю уравнение плоскости , для этого найду коофициент
D=-(Ax![]() +By
+By![]() +Cz
+Cz![]() )
)
D=-(0-4+9)=-5.
уравнение плоскости соответственно равно 4у+3z-5=0.
Ответ: 4у+3z-5=0.
№4. (2Д2). Найдите длину отрезка, отсекаемого от оси ординат плоскостью, содержащей прямую
![]() и параллельной вектору а=(1, 0, 2).
и параллельной вектору а=(1, 0, 2).
Чтобы найти расстояние отсекаемое от оси ординат плоскостью найду уравнение плоскости, зная два вектора параллельных плоскости и точку лежащую на этой плоскости пересекающей ось ординат:
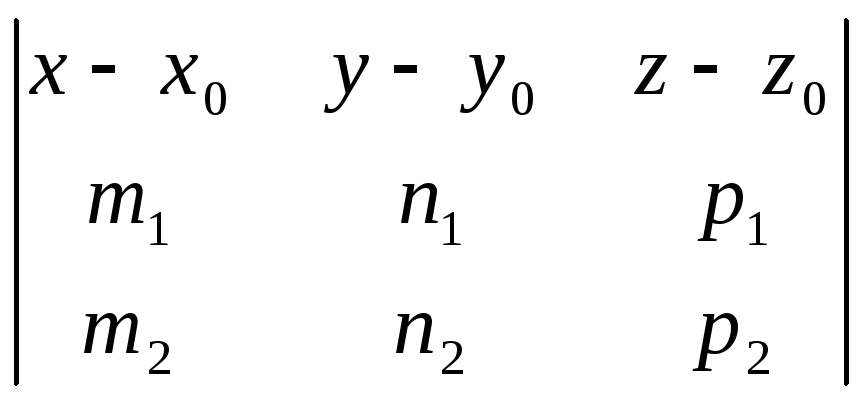 =
=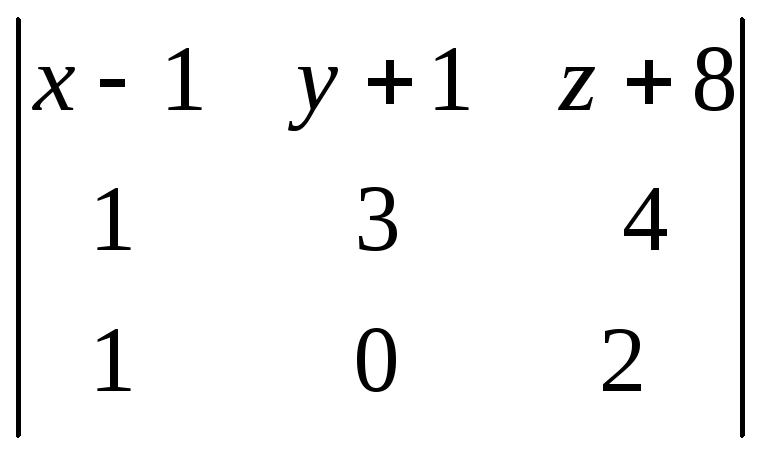 <=>
6(х-1)+4(у+1)-3(z+8)-2(y+1)=0
<=>
6(х-1)+4(у+1)-3(z+8)-2(y+1)=0
6x-6+2y+2-3z-2y=0,
6x+2y-3z-28=0.
Деля все уравнение плоскости на отрезки получу уравнение плоскости в отрезках откуда и найду искомую величину отрезка отсекаемого от оси ординат:
![]() Из уравнения видно что искомой величиной
является 14.
Из уравнения видно что искомой величиной
является 14.
Ответ: 14.
№5.(576). Прямая, проходящая через точку
Р(1, 2, 3) и пересекающая ось аппликат в
точке (0, 0, z![]() ),
параллельна плоскости 2х+у+z+6=0.
Найдите z
),
параллельна плоскости 2х+у+z+6=0.
Найдите z![]() .
.
Решение:
Прямая проходит через две точки Р(1, 2,
3) и (0, 0, z![]() ),
найду геометрический вектор параллельный
прямой и равный N(1, 2, 3- z
),
найду геометрический вектор параллельный
прямой и равный N(1, 2, 3- z![]() ),
найду вектор нормали для плоскости I(2,
1, 1), отсюда следует значение z
),
найду вектор нормали для плоскости I(2,
1, 1), отсюда следует значение z![]() ,
при котором векторы N
,
при котором векторы N
![]() I.
I.
2+2+3- z![]() =0,
=0,
z![]() =7.
=7.
№6(712.РП). Найдите координаты точки
пересечения с плоскостью х=1 прямой(l),
перпендикулярной плоскости 4x+2y+4z+5=0 и
пересекающей две заданные прямые
x+1=y=z(l![]() )
и 2x=2y=z+4(l
)
и 2x=2y=z+4(l![]() ).
).
1.Так как прямая перпендикулярна плоскости то находим ее вектор нормали N(4, 2, 4), а уравнение прямой можно записать как l:
![]()
2. Известно, что
![]() l,
M
l,
M![]()
![]()
![]() 4;
Значит l:
4;
Значит l:![]()
![]()
3. Найду точку пересечения прямой l
c прямой l![]() :
:
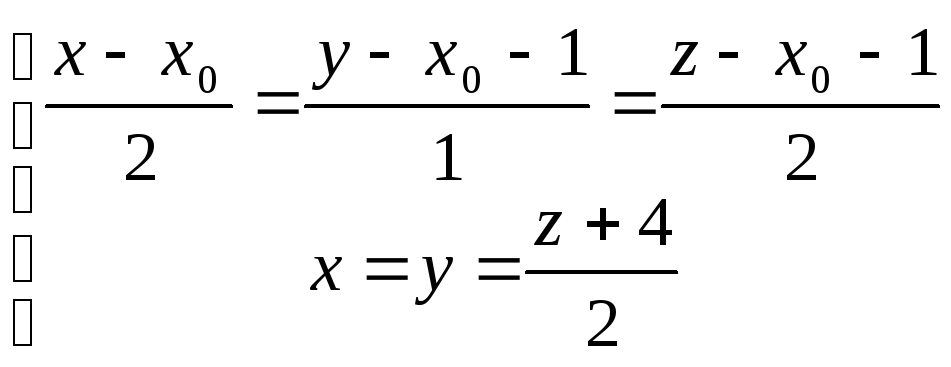
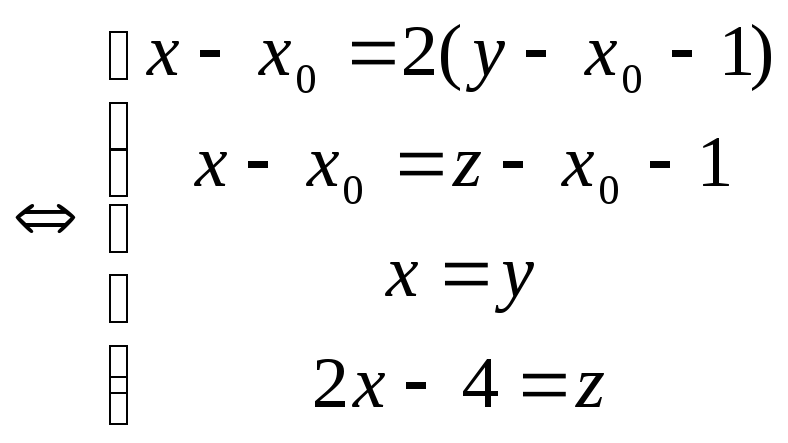
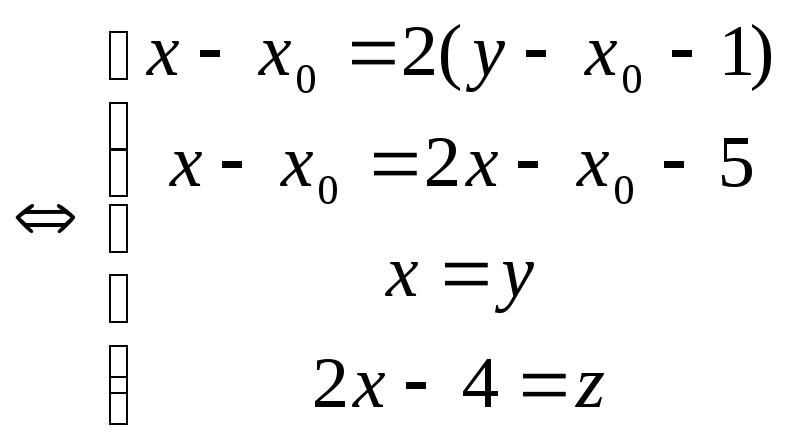
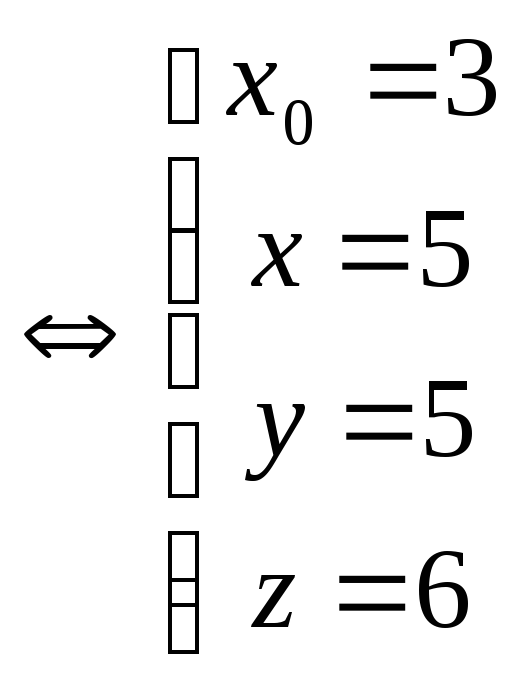 ,
,
т. е.получаю дветочки в которых прямая
l пересекает две оставшиеся прямые
![]()
![]()
4. Найду искомую точку пересечения:
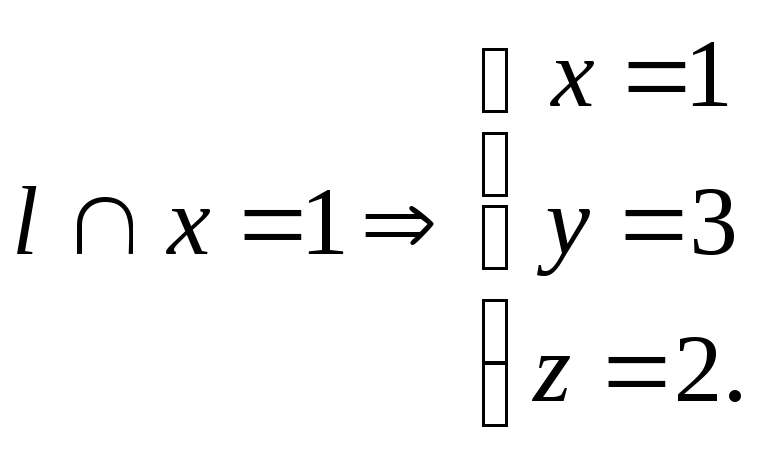
Ответ: M(1, 3, 2).
№7.(8Д1) Найдите радиус окружности, если известно, что она касается двух прямых 3х+4у-16=0 и 3х+4у+24=0.
Возьму точку на прямой М(х0, у0), тогда действуя по формуле найду расстояние
d(M,П), которое равно диаметру окружности:
![]() =
=![]() =8,
следовательно радиус равен 1/2d=8/2=4.
=8,
следовательно радиус равен 1/2d=8/2=4.
Ответ:4.
№8.Дана кривая
![]() .
.
8.1 Докажите что эта кривая- гипербола.
8.2(9С4.Б7). Найдите координаты её центра симметрии.
8.3(385.РП). Найдите действительные и минимальные полуоси .
8.4(9С6.БЛ). Запишите общее уравнение фокальной оси.
8.5 Постройте данную гиперболу.
8.1 Чтобы определить тип кривой составлю характеристическое уравнение квадратичной формы:
![]() -матрица квадратичной формы
-матрица квадратичной формы
![]() =
=![]()
![]() =-9,
=-9,
![]()
Так как собственные числа имеют разные знаки, то данное уравнение определяет кривую гиперболического типа.
Выделяя полные квадраты получаю :
![]()
Положим х1=х-2, а у1=у-4тогда уравнение прямой принимает канонический вид:
![]() =1.
Видим, что действительная ось а=3 а мнимая
b=1
=1.
Видим, что действительная ось а=3 а мнимая
b=1
Координаты точки О1 являющейся центром симметрии гиперболы равны (2, 4).
Уравнением фокальной оси является: y=4.
8.5
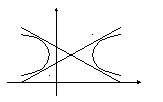

8.2Ответ: (2, 4).
8.3Ответ: действительная ось а=3 а мнимая b=1.
8.4Ответ:y=4.
№9.Дана кривая
![]() .
.
9.1 Докажите что данная кривая -порабола.
9.2(9Т7.РП). Найдите координаты ее вершины.
9.3(258). Найдите значение ее параметра р.
9.4(АР9.РП). Запишите уравнение ее оси симметрии.
9.5 Постройте данную пораболу.
9.1 Чтобы определить тип кривой составлю характеристическое уравнение квадратичной формы:
![]() -матрица квадратичной формы
-матрица квадратичной формы
![]() =
=![]()
![]() =0,
=0,
![]()
Так как произведение собственных чисел равно 0, то данное уравнение определяет кривую параболического типа.
Выделяя полные квадраты получаю :
![]()
![]() .
Видим, что параметр р параболы равен 2,
а вершина параболы О(0, 0), осью симметрии
является прямая y=0.
.
Видим, что параметр р параболы равен 2,
а вершина параболы О(0, 0), осью симметрии
является прямая y=0.
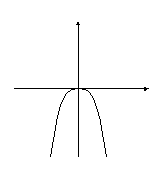

9.2Ответ: (0, 0).
9.3Ответ: р=2.
9.4Ответ: y=0.
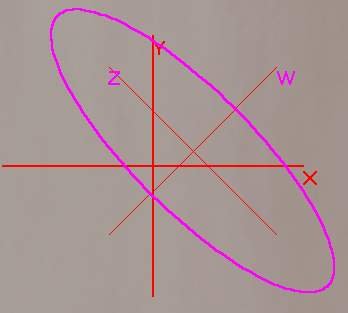
№10.Дана кривая
![]() .
.
10.1 Докажите, что эта кривая –эллипс.
10.2(9А0.БЛ). Найдите координаты центра его симметрии.
10.3(ПД1.РП).Найдите его большую и малую полуоси.
10.4(С82.РП). Запишите уравнение фокальной оси.
10.5. Постройте данную кривую.
10.1 Чтобы определить тип кривой составлю характеристическое уравнение квадратичной формы:
![]() -матрица квадратичной формы
-матрица квадратичной формы
![]() =
=![]()
![]() =9,
=9,
![]() =4
=4
Так как произведение собственных чисел больше 0, то данное уравнение определяет кривую эллиптического типа.
Найду собственные векторы матрицы В.
Для собственного числа
![]() =9
получаю систему:
=9
получаю систему:
![]() , эта система имеет бесконечное множество
решений выбираю значение для собственного
вектора
, эта система имеет бесконечное множество
решений выбираю значение для собственного
вектора
![]() (1,2).
Найду единичный собственный вектор
(1,2).
Найду единичный собственный вектор
![]() .
По свойству собственных векторов
симметричного оператора второй
собственный вектор
.
По свойству собственных векторов
симметричного оператора второй
собственный вектор
![]() =
=![]() .
.
Уравнение кривой в новых координатах
имеет вид: 9![]() .
.
Выделяя полные квадраты получаю :
9![]()
Совершу паралленый перенос осей координат
в новое начало
![]() по формулам :
по формулам :
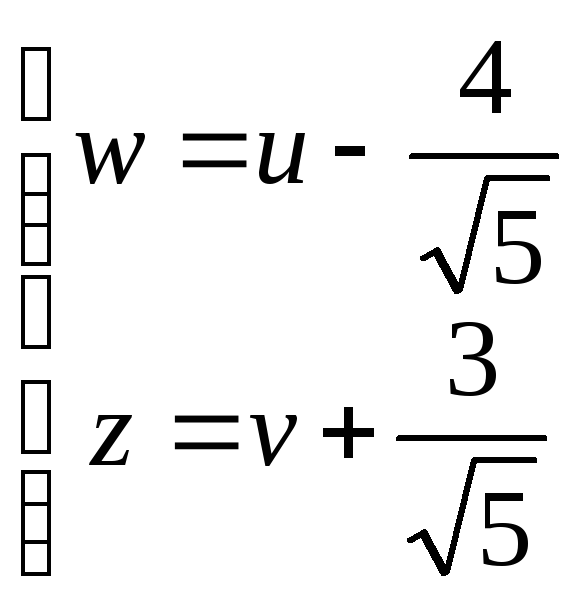 , тогда в системе координат (
, тогда в системе координат (![]() ,
w, z) уравнение прямой принимает канонический
вид:
,
w, z) уравнение прямой принимает канонический
вид:
![]() .
Видим, что 2-большая полуось, а 3-малая.
Центр симметрии имеет координаты
.
Видим, что 2-большая полуось, а 3-малая.
Центр симметрии имеет координаты
О(2,1), уравнение фокальной оси -2x+y+3=0.