2.6. Отношение эквивалентности
Бинарное отношение
называется
отношением эквивалентности, если оно
одновременно обладает тремя свойствами:
рефлексивностью, симметричностью и
транзитивностью, то есть если для любых
выполняется:
1.
― рефлексивность
2. если
,
то
― симметричность
3. если
и
,
то
― транзитивность.
Эквивалентные
отношения обозначаются так
или
,
что означает «
эквивалентно
в отношении
».
Например, быть
равным на множестве чисел,
быть подобным
на множестве геометрических фигур.
Непересекающиеся подмножества, на которые разбивается множество А от-
ношением
эквивалентности, называются классами
эквивалентности.
Таким образом, классы эквивалентности
– это непустые и непересекающиеся
множества, каждое из которых вместе со
своим любым элементом содержит также,
все элементы, эквивалентные эму по
отношению
и не содержит никаких других элементов
данного множества. Множество классов
эквивалентности множества А
относительно
отношения
называется фактор-множеством
и обозначается
.
Пример.
Отношение между целыми числами
и
,
выражаемое равенством
целые
числа называется отношением сравнения
и
по модулю
и записывается, как
.
Это отношение является отношением
эквивалентности. Действительно,
1.
- рефлексивность
2.
- симметричность
3. транзитивность
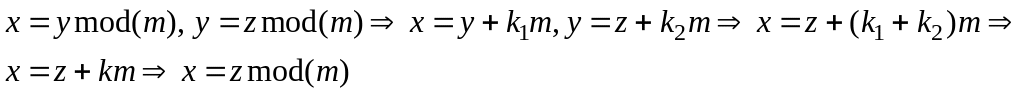
Множество целых
чисел
разбивается этим отношением на
классов
,
,
,
…
.
В частности, при
,
происходит разбиение множества
на множество
четных и нечетных
чисел, при
― на множество чисел, кратных трем и
дающих
при делении на три в остатке 1 и 2.
2.7. Отношение порядка
Бинарное отношение
называется отношением
порядка на
множестве А,
если оно обладает свойствами
антисимметричности и транзитивности.
Для произвольного отношения порядка
принято обозначение
,
означающее предшествование.
Множество
,
которое обладает отношением порядка,
называется упорядоченным.
Рефлексивное
отношение порядка называют отношением
нестрого порядка и обозначают знаком
«
».
Антирефлексивное
отношение порядка называют отношением
строго порядка и обозначают знаком «
».
Говорят, что на множестве задано отношение полного (частичного) порядка, если сравнимы все (не все) элементы данного множества.
Множество , на котором установлено отношение полного (частичного) по-
рядка называется вполне (частично) упорядоченным.
Отношение нестрого порядка должно удовлетворять трем условиям: рефлексивности, антисимметричности и транзитивности.
Отношение нестрого
порядка есть объединение отношения
строгого порядка и отношение
тождественности. Каждому отношению
порядка
на
множестве
можно поставить в соответствие обратное
отношение порядка
.
Например, отношение больше
и меньше
на множестве действительных чисел.
Для связного
отношения
на множестве
существует ему противоположное
,
причем если
отношение нестрого порядка, то
― отношение строго порядка и наоборот
(например,
и
на множестве действительных чисел).
Пусть
– упорядоченное
множество с отношением строго порядка
.
Об упорядоченной паре
говорят, что элемент
предшествует элементу
.
Пусть – вполне упорядоченное множество. Тогда, если для элемента не
нашлось предшествующего, то он называется минимальным (инфинум), то есть не существует элементов меньших чем . Символически это записывается так
.
На множестве натуральных чисел выполняется лишь свойство антисимметри-чности и транзитивности. Поэтому на нем установлено отношение строго порядка: для любой пары натуральных чисел единица является предшествующим числом, то есть минимальным. Можно доказать, что конечное вполне упорядоченное множество содержит единственный минимальный элемент.
Минимальным
(максимальным)
элементом множества
,
на котором задано отношение нестрого
порядка, называют такой элемент
,
что для всякого элемента
,
который сравнивается с
,
имеет место неравенство
.
Например, на
множествах целых, рациональных и
действительных чисел отношения «
»
есть отношения нестрого полного порядка,
а отношения «
»
есть отношения строго полного порядка.
Отношение «
»
есть отношение нестрого частичного
порядка на множестве
(булеан).
Если
― отношение частичного порядка на
множестве
,
то при
и
мы называем
предшествующим
элементом
или предшественником,
а
―
последующим.
У произвольно взятого элемента
может
быть много предшествующих элементов.
Однако если
предшествует
,
и не существует таких элементов
,
для которых
и
,
мы называем
непосредственным предшественником
и пишем
.
Непосредственных предшественников можно условно изобразить с помощью графа, известного как диаграмма Хассе. Вершины графа изображают элементы частично упорядоченного множества , и если , то вершина помещается ниже вершины и соединяется с ней ребром.
Диаграмма Хассе дает полную информацию об исходном частичном порядке.
Пример.
Дано, что отношение «…делитель…»
определяет частичный порядок на множестве
.
Составьте таблицу предшественников и
непосредственных предшественников,
после чего постройте диаграмму Хассе.
элемент |
предшественник |
непосредственный предшественник |
1 |
нет |
нет |
2 |
1 |
1 |
3 |
1 |
1 |
6 |
1,2,3 |
2,3 |
12 |
1,2,3,6 |
6 |
18 |
1,2,3,6 |
6 |
Рис. 10
Линейным порядком на множестве называется отношение частичного порядка, при котором из любой пары элементов можно выделить предшествующий и последующий.
Всякий частичный порядок на конечном множестве может быть доведен до полного.
В случаях, когда речь идет про множество людей, имеют место отношения доминирования.
Бинарное отношение
называют отношением доминирования,
если оно антирефлексивно и антисимметрично.
Говорят, что
доминирует над
(
),
когда
в каком либо смысле преобладает над
.
Например, если внутри организации существует отношение подчинения, то
для двух членов организации один доминирует над другим, если он им руководит.