Можно ли сказать, что определение n-ой степени некоторого числа формально совпадает с определением умножения некоторого числа на число n?
Да, можно. С формальной точки зрения эти определения совершенно одинаковы. И в том и другом случае используется конструкция многократного применения одной и той же операции к одному числу. При умножении – используется операция сложения, при возведении в степень – умножение.
Возведение в степень можно рассматривать как операцию, примененную к двум числам k и n. Определяя подобным образом умножение мы обнаружили, что несмотря на то, что сомножители в операции умножения имеют разный смысл сама операция умножения переместительна (коммутативна). Является ли переместительной операция возведения в степень?
Нетрудно
убедится при помощи простых примеров,
что операция возведения в степень не
является переместительной:
. Здесь мы видим интересный пример того,
как применение одной и той же логической
конструкции для определения одной
операции на основе другой (исходной)
операции может приводить к операциям
обладающими разными свойствами.
Каковы основные свойства операции возведения в степень?
1 -
степень произведения двух
чисел равна произведению степеней этих
числе с тем же показателем.
Доказывается непосредственно из определения.
2. -
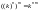степень степени некоторого
числа k
равна степени этого числа с показателем
равным произведению соответствующих
показателей. Доказывается непосредственно из определения.
3 -
произведение степеней числа
k
равно этому числу в степени являющейся
суммой показателей степеней сомножителей.
Доказывается непосредственно из определения.
4 -
Если n
> m,
то частное степеней числа k
равно этому числу в степени равной
разности показателя числителя и
показателя
знаменателя. Доказывается непосредственно из определения.
5. -
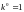при
Любое не равное нулю натуральное число
в нулевой степени равно 1.
Это свойство
является прямым следствием свойства
2. Действительно,
таким образом, видим,
что
Что такое корень n-ой степени из натурального числа k?
Корнем n-ой степени называется такое натуральное число m, что m в степени n равно k. Это искусственная конструкция. Очевидно что эта операция выполнима не всегда.
Что означает, что одно натуральное число больше другого?
Говориться, что число n больше числа m, если в конечном множестве отдельных предметов, которое описывается числом n найдется не равная ему часть,
которая описывается числом m .
Каким образом записывается отношение больше? Как называется знак, при помощи которого записывается отношение больше?
Для записи этого отношения используется знак < или >. При этом возле широкой части знака ставится то число, которое больше из двух, а возле узкой
части знака второе число, которое называется меньшим из двух. Сам знаки называются знаками неравенства, и любой из них называется противоположным по
отношению к другому.
Как называется запись со знаком неравенства показывающая, что одно число больше другого?
Запись (n < m) использующая этот знак, когда по обеим сторонам знака стоят некоторые числа называется неравенством и читается двумя равнозначными
способами: «n меньше m» или «m больше n».
Как называются числа-участники отношения «больше» или «меньше» в том случае, когда отношение истинно?
Если пара чисел находится в отношении больше или меньше, то такие числа называются сравнимыми.
Можно ли отношение «больше» формально определить используя операцию сложения?
Да, можно. Определим, что одно натуральное число n больше другого натурального числа m, если найдется такое натуральное число k, что n = m + k.
Это определение равнозначно определению данному ранее в пункте 17.
Что имеется в виду или какая ситуация описывается, когда говорится о том, что одно натуральное число больше другого на некоторое третье натуральное
число – например: «одиннадцать больше восьми на три»
Такое выражение говорит о том, что во-первых одно число больше другого, а во-вторых, что ко второму надо прибавить три чтобы получить первое.
Сколькими способами можно выстроить в очередь (одно за другим) все натуральные числа?
Число способов выстроить в очередь или упорядочить натуральные числа бесконечно. Каждый из таких способов называется порядком.
Какой порядок (способ выстраивания в очередь) на натуральных числа называется естественным?
Способ, при котором каждое следующее число в очереди на единицу больше предыдущего называется естественным порядком натуральных чисел?
Каковы свойства отношения «больше» по отношению к арифметическим операциям на натуральных чисел?
1. Для любых двух не равных натуральных чисел n и m, либо n < m , либо m < n это свойство называется свойством полной сравнимости
2. Если n < m и m < k, то n < k если число больше большего из двух то оно больше и меньшего из двух (транзитивность)
3. Если n < m , а k – любое число, то n + k < m + k если к обеим частям неравенства прибавить одно и то же число неравенство сохраниться.
Сохранение неравенства при прибавлении любого числа.
4. Если n < m , а k – любое число, то n - k < m - k если из обеих частей неравенства вычесть одно и то же число неравенство сохраниться.
Сохранение неравенства при вычитании любого числа. (в случае, если вычитание выполнимо)
5. Если n < m , а k – любое число, то n * k < m * k если обе части неравенства умножить на одно и то же число неравенство сохраниться.
Сохранение неравенства при умножении на любое число.
6. Если n < m , а k – любое число, то n : k < m : k если обе части неравенства разделить на одно и то же число неравенство сохраниться.
Сохранение неравенства при делении на любое число.( если деление возможно)
7. Если
n
< m
, а
k
0 любое число, то
если
обе части неравенства возвести в одну
и ту же ненулевую степень то неравенство
сохранится.
Сохранение неравенства при возведении в степень.
8. Если
n
< m
, а
k
0 любое число, то
Из
двух степеней натурального числа k
больше та, показатель которой больше.
.
Что имеется в виду, когда говорят, что одно число находится между двумя другими?
Если для двух чисел m и n, m < n, то говорят, что некоторое третье число k находится между ними если одновременно выполняется двойное неравенство :
m < k < n.
Если натуральные числа расположены в естественном порядке, то в каком направлении их можно перечислять бесконечно?
В направлении возрастания.
ВОПРОСЫ ДЕЛИМОСТИ
Какое число называется делителем натурального числа?
Натуральное число q называется делителем натурального числа n, если найдется такое натуральное m, что n = qm. Число m в этом случае называется частным от деления n на q.
Что можно сказать о количестве делителей не равных единице и самому исходному числу у произвольного натурального числа?
Из самого смысла делителя ясно, что количество их ограничено. Хотя бы самим числом n. Можно также увидеть, что количество делителей любого числа не может быть больше половины исходного числа. Действительно, если предположить, что делителей у некоторого числа n больше чем n/2, то самый большой из них должен быть больше чем n/2. Однако в этом случае исходное число не сможет на него разделиться.
Что такое общий делитель двух или нескольких натуральных чисел?
Любое натуральное число, которое является одновременно делителем каждого из двух или нескольких чисел называется общим делителем этих чисел.
Что такое наибольший общий делитель двух или нескольких натуральных чисел? Как он обозначается?
Наибольший из общих делителей двух или нескольких натуральных чисел называется наибольшим общим делителем этих чисел и обозначается НОД( ), где в скобках, через запятую перечисляются исходные числа..
Каково главное свойство наибольшего общего делителя нескольких натуральных чисел?
Главное свойство НОД нескольких натуральных чисел заключается в том, любой другой общий делитель этих чисел является делителем НОД.
Какие числа называются взаимно-простыми?
Числа, НОД которых равен 1 называются взаимно простыми.
В каком случае мы может утверждать, что дробь несократима?
Числовая дробь несократима в том, и только в том случае, когда числитель и знаменатель взаимно-простые.
Может ли любое рациональное число быть представлено в виде несократимой дроби?
Да, может. Это следует из того, что любое число имеет конечное число делителей.
Является ли представление рационального числа в виде несократимой дроби единственным?
Да, представление любого рационального числа в виде несократимой дроби является единственным. Это следует из того, две дроби равны по определению в том и только в том случае, когда одна может быть получена из другой путем умножения числителя и знаменателя на одно и то же число.
Какое число называется кратным некоторого натурального числа?
Кратным некоторого натурального числа m называется любое натуральное число, полученное путем умножения m на любое натуральное число.
Что можно сказать о количестве кратных произвольно заданного натурального числа?
Кратных любого натурального числа бесконечное множество.
Как записывается формула для записи всех кратных данного числа m?
Для
записи всех кратных данного числа m
принята такая форма : K
= m*k,
где k
N
= { 1, 2, 3,…..}
Какое число называется общим кратным двух или нескольких натуральных чисел?
Число являющееся одновременно кратным двух или нескольких натуральных чисел называется их общим кратным.
Что такое наименьшее общее кратное двух или нескольких чисел? Как оно обозначается?
Наименьшее среди общих кратных двух или нескольких натуральных чисел называется наименьшим общим кратным этих чисел и обозначается НОК( ), где в скобках, через запятую перечисляются исходные числа.
Каково главное свойство наименьшего общего кратного нескольких чисел?
Главное свойство НОК нескольких натуральных чисел заключается в том, что любое общее кратное этих чисел делится на НОК этих чисел.
Что такое простое число?
Число называется простым если оно не имеет делителей, отличных от единицы и самого себя.
Как звучит теорема о представлении любого числа в виде произведения степеней простых чисел?
Любое натуральное число представимо в виде произведения степеней простых чисел. Такое представление с точностью до порядка сомножителей единственно.
Как найти представление натурального числа в виде произведения степеней простых чисел?
Для того, чтобы найти представление числа в виде степеней простых чисел необходимо иметь перед собой таблицу простых чисел, расположенную в порядке возрастания. Первым шагом пробуется делителем первое простое число. Если оно не подходит, то пробуется второе число в таблице и так далее. Если число подходит в качестве делителя, то выписываем его, а частное рассматриваем снова как исходное число и возвращаемся к первому шагу. Через конечное число шагов будем иметь произведение некоторого конечного множества простых чисел. Заменяя произведения одинаковых из них соответствующими степенями получим искомое представление.
Как найти НОД нескольких чисел?
Для того чтобы найти НОД нескольких чисел надо найти представление каждого из них в виде произведения степеней простых чисел и затем взять произведение общих для обоих представлений простых чисел, каждое в наименьшей из имеющихся степеней.
Как найти НОК нескольких чисел?
Для того чтобы найти НОК нескольких чисел надо найти представление каждого из них в виде произведения степеней простых чисел и затем взять
произведение всех имеющихся во всех представлениях простых чисел, каждое в наибольшей из имеющихся степеней.
Какова формула для записи всех четных чисел?
K = 2*k, где k N = { 1, 2, 3,…..}
Какова формула для записи всех нечетных чисел?
K = 2*k-1, где k N = { 1, 2, 3,…..}
Какова формула для записи квадратов всех чисел?
K
=
,
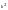где k
N
= { 1, 2, 3,…..}
Какова формула для записи квадратов всех четных чисел?
K
=
, где k
N
= { 1, 2, 3,…..}
Какова формула для записи квадратов всех нечетных чисел?
K
=
, где k
N
= { 1, 2, 3,…..}
Как формулируется основная теорема арифметики или теорема о делении с остатком?
Каковы бы ни были два натуральных числа n и m, обязательно найдутся такие числа q и r, где r < m, что число n может быть представлено в виде
n = m* q + r. Причем показанное представление единственно.
ЦЕЛЫЕ ЧИСЛА