Контрольная работа 1 / 1- 9_Высшая математика_4

Томский межвузовский центр дистанционного образования

Томский государственный университет

систем управления и радиоэлектроники (ТУСУР)

Контрольная работа № 1

Вариант 1.9

по дисциплине «Высшая математика-1»

Линейная алгебра и аналитическая геометрия.

Вариант 1.9

1.Найдите матрицу C = AB-BA , если A = , B = .

Решение. Так как AB ≠ BA , то АВ и BA , находим отдельно.

АВ = =,

BA = =,

C = - =.

Ответ: C =.

2.Вычислите определитель D = .

Решение. Пользуясь теоремой 2 (с.17),вычисление определителя можно свести к вычислению четырёх определителей третьего порядка. Число этих определителей можно снизить до одного, получив, пользуясь свойствами определителя, в какой-либо строке или столбце три нулевых элемента.

D = === -= - (-3) (-6)-

- (-5) (-6) = 12

(Строка 2 просуммирована со строкой 1, умноженной на -1),

(Строка 3 просуммирована со строкой 1, умноженной на -2),

(Строка 4 просуммирована со строкой 1, умноженной на -3);

(Строка 2 просуммирована со строкой 1, умноженной на -1),

(Строка 3 просуммирована со строкой 1, умноженной на -2).

Ответ: D = 12.

3. Решите матричное уравнение

X · =.

Решение. Матричное уравнение можно записать в виде X · A = B.

Обозначим

A =, B =.

Находим det A = = = ¹⁺¹ = 1.

(Строка 2 и 3 просуммирована со строкой 1, умноженной на -2).

Матрица A невырожденная, а потому имеет обратную A^-1.Элементы обратной матрицы находятся по формуле .

= (-1)¹⁺¹ = 7, = (-1)¹⁺² = -1, = (-1)¹⁺³ = -2.

= (-1)²⁺¹ = -4, = (-1)²⁺² = 1, = (-1)²⁺³ = 1.

= (-1)³⁺¹ = -2, = (-1)³⁺² = 0, = (-1)³⁺³ = 1.

Таким образом;

A^-1 = .

Находим X по формуле X = B ∙ A^-1:

X = ∙ = =

= = .

Проверка X ∙ A = B:

X ∙ A = ∙ =

= =

= = .

Матрица X удовлетворяет данному уравнению, следовательно, найдено верно.

Ответ: X =.

4. При каком значении параметра p, если оно существует строки матрицы

A = линейно зависимы.

Решение. Для того чтобы система векторов a_1, a_{2 , …,} a_{n ,} была линейно зависимой, необходимо и достаточно, чтобы хотя бы один из векторов бы линейной комбинацией других. (теорема 1. стр. 23) Итак, находим вектора a = (1, 2, -1, 3, -2,),

b = (2, 4, 5, 4, 3,),

d = (1, p, 6, 1, 5,).

Обозначим λ₁ и λ₂ коэффициенты линейной комбинации, с помощью которых четвёртая строка выражается через первые две, т.е. aλ₁ + bλ₂ = d.

λ₁ (1, 2,-1, 3,-2) + λ₂ (2, 4, 5, 4, 3,) = (1, p, 6, 1, 5).

Получаем систему

λ₁ + 2λ₂ = 1

2λ₁ + 4λ₂ = p

-1λ₁ + 5λ₂ = 6

3λ₁ + 4λ₂ = 1

-2λ₁ + 3λ₂ = 5

-1λ₁ + 5λ₂ = 6

Решая систему 3λ₁ + 4λ₂ = 1 находим λ₁ = 1, λ₁ = 1

-2λ₁ + 3λ₂ = 5

При этих значениях λ₁ и λ₂ первое уравнение превращается в тождество, так как -1 + 2 = 1.

Из второго уравнения находим p = -2 + 4 = 2.

Матрица A является линейно зависимой при p = 2так как четвёртая строка матрицы является линейной комбинацией первых двух строк.

Ответ: p = 2

5. Относительно канонического базиса в R₃ даны четыре вектора: f₁(1, 2, 3), f₂(2, 3, 1), f₃(1, 1, -3), x(2, 4, 1). Докажите, что векторы f_1, f_2, f₃ можно принять за новый базис в R₃. Найдите координаты вектора x в базисе f_i.

Решение. Составим матрицу C, записав в её столбцах координаты векторов f_1, f_2, f₃:

C =

det = = = 1(-1)¹⁺¹ = (-1)(-6) - (-1)(-5) = 1.

Так как det C 0, то векторы f_1, f_2, f₃ линейно независимы, а потому могут быть приняты в качестве базиса в R₃. Матрица C невырожденная, потому имеет обратную C^-1.

= (-1)¹⁺¹ = -10

Таким образом, применяя формулу, находим C^-1.

C^-1 = .

Новые координаты вектора x, находим по формуле

= .

Ответ: координаты вектора x =.

6. Докажите, что система имеет единственное решение. Неизвестное x₃, найдите по формулам Крамера. Решите систему методом Гаусса.

Решение. Вычислим определитель системы

D =

Находим x₃, методом Крамера

D₃ =

.

Решаем систему методом Гаусса. Записываем расширенную матрицу системы и преобразуем её к трёугольному виду, действуя только со строками.

Таким образом, данная система эквивалентна системе

из которой находим х₄ = - 1;

- 3х₃ = 2 – 5 = - 3, х₃ = 1;

х₂ = 7 – 2 – 6 = 1, х₂ = 1;

х₁ = - 3 – 4 + 8 = 1, х₁ = 1.

Получено решение:(1, 1, 1, -1).

Ответ: (1, 1, 1, -1).

7. Дана система линейных уравнений .

Докажите, что система совместна. Найдите её общее решение. Найдите частное решение, если х₃ = х₄ = -1.

Решение. Примем к этой системе метод Гаусса. Запишем расширенную матрицу системы и преобразуем её, действуя только со строками, к виду, из которого легко увидеть базисный минор.

Отсюда следует что ранг основной и расширенной матрицы равен 2, следовательно, система совместна. В качестве базисного минора выберем , т.е. неизвестное х₁ и х₂ приняты в качестве зависимых, а х₃ и х₄ – в качестве свободных.

Данная система эквивалентна системе

Выражаем зависимые переменные через свободные:

- общее решение системы. Пологая, что х₃ = х₄ = -1, находим х₁ = 1, х₂ = 1.

Мы получили частное решение (1, 1, -1, -1).

8. Дана система линейных однородных уравнений

Докажите, что система имеет нетривиальное решение. Найдите общее решение. Найдите какую-нибудь фундаментальную систему решений.

Решение. Исследуя систему методом Гаусса. Запишем её матрицу и, действуя только со строками, упрощаем её, не меняя ранга.

Мы видим, что две последние строки пропорциональны. Одну из них можно вычеркнуть, не меняя ранга матрицы. Ранг матрицы равен двум, следовательно, он меньше числа неизвестных. По теореме 2 (стр. 45) система имеет нетривиальное решение. Обведённый минор можно принять в качестве базисного. При таком выборе базисного минора неизвестные х₁ и х₂ – зависимые, а х₃ и х₄ – свободные. Данная система эквивалентна

Выражаем зависимые переменные через свободные, находим общее решение:

Фундаментальная система решений содержит 4 – 2 = 2 решений (разность между числом неизвестных и рангом). Получим два частных линейно независимых решения, придавая поочерёдно свободным неизвестным значения (1, 0), (0,1)

(2, 0, 1, 0)

(-1, 1, 0, 1)

Эти решения образуют фундаментальную систему решений.

9. Найдите (a, b), если а = 5р + 2r, b = p - r, |p| = , |r| = 1, (p^{^},r) = 45^о.

Решение. (a,b) = (5p + 2r, p - r) = 5(p, p) + 2(r, p) - 5(p, r) - 2(r, r) = 5|p²| - 3|p,r| ∙ cos 45 - 2|r²| = 5∙2 – 3∙ ∙ 1 ∙ - 2 ∙ 1 = 10 – 3 – 2 = 5.

Ответ: 5.

10. Вычислите высоту треугольника ABD, опущенную из точки D, если A(1,2,2); B(3,-2,-2); D(1,-4,-1).

Решение. Поскольку высота треугольника вычисляется по формуле , то сперва, находим S площадь, S = 1/2 |[AB, AD]|

AB = (2, - 4, - 4);

AD = (0, -6, -3).

[AB, AD] = .

|[AB, AD]|=/

.

h =

h = 3.

Ответ: h = 3.

11. Линейный оператор А действует в R₃  R₃ по закону Ах = (3х₁, 2х₁, + х₃, х₁ + 2х₂+х₃), где х(х₁, х₂, х₃) – произвольный вектор. Найдите матрицу А этого оператора в каноническом базисе. Докажите, что вектор х(0, 1, 2) является собственным для матрицы А. Найдите собственное число , соответствующее вектору х. Найдите другие собственные числа, отличные от . Найдите все собственные векторы матрицы А и сделайте проверку.

Решение. Так как А(1, 0, 0) = (3, 2, 1), А(0, 1, 0) = (0, 0, 2), А(0, 0, 1) = (0, 1, 1), то записав в столбцы координаты полученных векторов, найдём матрицу А: А = .

Проверим, что вектор х = (0, 1, 2) является собственным матрицы А. Находим

Ах = ∙ = .

Так как Ах = 2х, то отсюда следует, что вектор х(0, 1, 2) собственный и отвечает собственному числу .

Чтобы найти все другие собственные числа, составляем характеристическое уравнение

|А - Е| = =

.

Нам уже известно, что число = 2 – корень этого уравнения. Разделив многочлен

на (), получим . Другие собственные числа найдём, решая уравнение = 0

Итак собственными числами являются (-1, 3, 2).

Находим собственные векторы, отвечающие этим собственным числам.

. Собственные векторы, отвечающие этому собственному числу, образуют фундаментальную систему решений системы линейных однородных уравнений

,

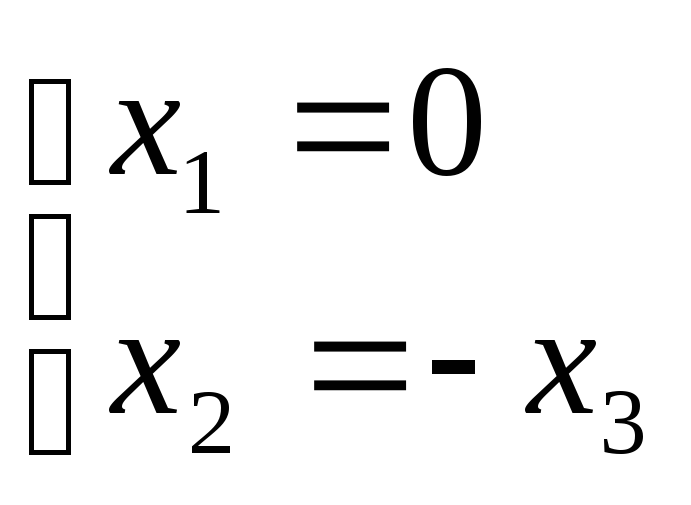- является общим решением системы. Положив, например, х₂ = 2, найдём собственный вектор х = (0, 2, -2).

Проверка: ∙, т. е. вектор (0, 2, -2) является собственным и отвечает собственному числу .

Собственные векторы, отвечающие этому собственному числу, образуют фундаментальную систему решений системы линейных однородных уравнений

. Ранг матрицы этой системы, очевидно, равен двум. Поэтому фундаментальная система решений состоит из одного решения. Таким образом,

- является общим решением системы. Положив, например, х₂ = 5, найдём собственный вектор х = (4, 5, 7).

Проверка: ∙ т. е. вектор (4, 5, 7) является собственным и отвечает собственному числу

Учебное пособие Л. И. Магазинников, А. Л. Магазинникова.

1 марта 2004 г.