Обыкновенные дифференциальные уравнения первого порядка с разделяющимися переменными.
Определение 3.1 Дифференциальные уравнения первого порядка (2.2) и (2.3) называются уравнениями с разделяющимися переменными ,если они представимы в виде
(3.1)
или
(3.2).
В уравнениях (3.1) и (3.2) разделим переменные и проинтегрируем.
или
.
После интегрирования получим либо общий интеграл, либо общее решение.
Если заданы
начальные условия
,
то найдем частное решение, подставив
С
,
найденное по начальным условиям, вместо
С .
Пример 3.1
Решить задачу Коши
.
Решение:
-это
уравнение с разделяющимися переменными,
т.к.
.
Разделим переменные:
и проинтегрируем
или
- общий интеграл.
Решим задачу Коши:
В общий интеграл подставим начальные
условия:1
-0
=2С,
С=
.
Запишем частный интеграл, подставив
С=
в общий интеграл дифференциального
уравнения.
-
частный интеграл.
Геометрический смысл дифференциального уравнения и его решений.
Геометрически
решение данного дифференциального
уравнения
представляет собой семейство равносторонних
гипербол
,
а частный интеграл, соответствующий
решению задачи Коши
-
это гипербола
,
проходящая через заданную точку.(Рис.2)
Пример 3.2
Решить уравнение
.
Решение.
Разделим обе части
уравнения на
,
получим уравнение с разделяющимися
переменными
.
Проинтегрируем это уравнение и получим
- общий интеграл дифференциального
уравнения
.
Потенцируя последнее
равенство, получим общее решение
уравнения
,
.Заметим
, что решение
входит в общее решение при С=0.
К уравнениям с
разделяющимися переменными приводятся
уравнения вида
при помощи подстановки
,
где
-
постоянные.
Подставим
в уравнение
.Получим
,
т.е.
.
Проинтегрируем и получим
.
В общем интеграле вернемся к прежней
переменной
.
Пример 3.3.
Решить задачу Коши
.
Решение.
Пусть
,
тогда
,
или
.
Разделим переменные и проинтегрируем
.
Потенцируем
полученное уравнение:
или
.
-
общее решение.
Найдем частное решение:
.
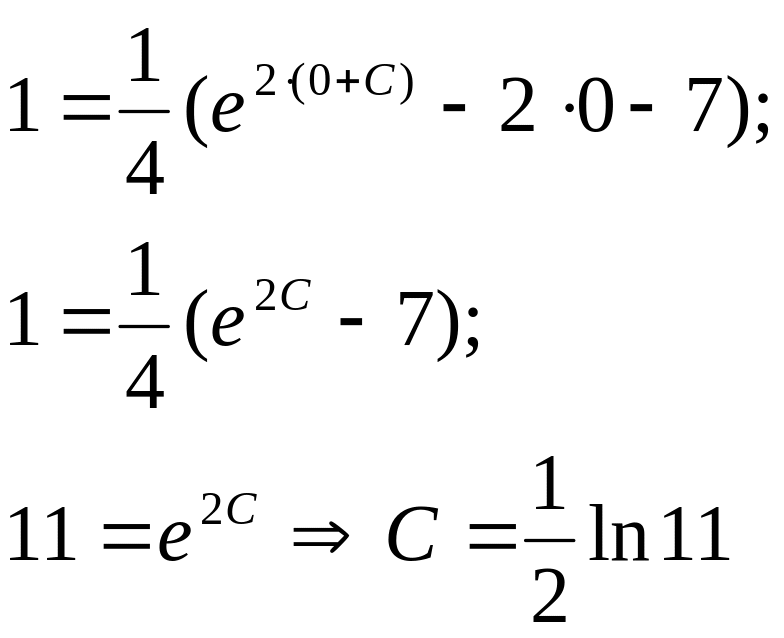Подставим С в общее
решение.
-
частное решение.
Задачи для самостоятельного решения
Найти общее (частное) решение уравнения
3.1.
.
3.2.
,
3.3.
3.4.
;
3.5.
Ответы:
3.1.
;
3.2.
;
3.3.
3.4.
;
3.5.
Однородные дифференциальные уравнения первого порядка.
Определение
4.1.Функция
двух переменных
называется однородной
функцией степени
относительно
и
, если для любого
выполняется равенство:
.
При
является однородной функцией нулевого
порядка.
Определение 4.2.
Однородными
дифференциальными
уравнениями
называются уравнения вида
(4.1),
где
-
однородная функция нулевого порядка.
или
(4.2),
где
и
- однородные функции одинакового порядка
однородности относительно
и
.
Однородные уравнения
(4.1) и (4.2),приводятся к уравнениям с
разделяющимися переменными с помощью
замены
,
при этом
Пример 4.1.
Решить задачу Коши
.
Решение:
.
Проверим эти функции на однородность.
.
и -однородные функции первого порядка, значит уравнение является однородным.
Сделаем замену
,
и подставим в исходное уравнение.
;
;
.
Получили дифференциальное уравнение 1-ого порядка с разделяющимися переменными.
Разделим переменные:
и проинтегрируем
.Тогда
или
.
-
общее решение.
Найдем частное
решение, используя начальные условия
.
Подставим С в общее решение:
-частное
решение.
Пример 4.2. Решить
уравнение
.
Решение.
Убедимся, что это
однородное уравнение
-однородная
функция нулевого порядка.
Для решения
уравнения выполним замену:
;
и подставим в уравнение:
-
уравнение с разделяющимися переменными.
.
Интеграл, стоящий в правой части уравнения разложим на простые дроби и проинтегрируем
,
вернемся к
.
;
-общий
интеграл.
К однородным
дифференциальным уравнениям первого
порядка приводятся уравнения вида:
,
(4.5)
где
-вещественные
постоянные.
Если прямые
и
пересекаются в точке
,
то вводятся новые переменные
.
Если прямые
параллельны, то подстановка
,
приводит к уравнению с разделяющимися
переменными.
Пример 4.3.Решить
уравнение
.
Решение:
Прямые
и
пересекаются, т.к. векторы
не
параллельны (
)
.
Найдем их точку пересечения:
т.е.
.
Введем новые переменные
.
Учитывая, что
Исходное уравнение принимает вид:
или
-
это однородное уравнение вида (4,3).
Выполним подстановку:
,разделим
переменные
или
-общий
интеграл.
Задачи для самостоятельного решения.
Найти общее (частное) решение уравнения
4.1-
4.2-
4.3-
4.4-
Ответы:
4.1-
4.2-
4.3-
4.4-
