
- •Пример 2 Центральное растяжение - сжатие (стержневая система)
- •Решение
- •Пример 3 Кручение вала круглого поперечного сечения
- •Пример 4 Плоский изгиб
- •Задача 5 Геометрические характеристики плоского сечения
- •Решение
- •1. Главными центральными осями плоского сечения называют оси проходящие через центр сечения, относительно которых центробежный момент сечения равен нулю.
- •4. Наконец можно перейти к определению положения главных центральных осей плоской фигуры и вычислению осевых моментов относительно этих осей.
- •Задача №6
- •Решение
- •3. Необходимые для решения задачи перемещения определим, используя интеграл Мора:
- •Двутавры стальные горячекатаные сортамент гост 8239-89
- •7. Приведем, как пример, проверку условия прочности в сечении, где , (это сечение над опорой ):
Задача 5 Геометрические характеристики плоского сечения
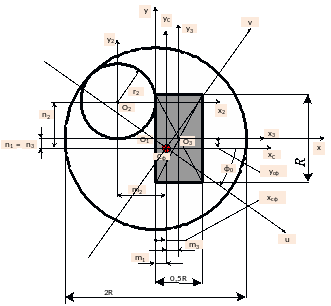
Для плоской фигуры, представленной на рисунке 5.1а), определить положение главных центральных осей и вычислить осевые моменты фигуры относительно этих осей.
Плоская фигура - это тонкая однородная пластина, ослаблена отверстием (на рисунке показано белым цветом) и усилена плоской накладкой (на рисунке отмечена густой штриховкой).
Рис. 5.1а)
|
Рис. 5.1б)
|
Рис. 5.1в)
|
Рис. 5.1г)
|
Рис. 5.1
Решение
1. Главными центральными осями плоского сечения называют оси проходящие через центр сечения, относительно которых центробежный момент сечения равен нулю.
Алгоритм решения задачи предполагает:
- определение положения центра сечения;
- расчет геометрических характеристик сечения относительно удобных центральных осей;
- расчет положения главных центральных осей и определение осевых моментов сечения относительно этих осей.
Как правило, для упрощения решения задачи сложное сечение делят на части - простые фигуры, для которых известны или могут быть достаточно легко определены геометрические характеристики относительно удобных осей координат.
Исходное
сечение можно рассматривать как
совокупность трех фигур: из круга (фигура
1 на рис. 5.1б) вырезают круг меньшего
диаметра (фигура 2 на рис. 5.1в) и накладывают
прямоугольник (фигура 3 на рис. 5.1г).
Удобные для решения задачи системы
координат
 показаны на рисунках.
показаны на рисунках.
2. Положение центра плоского составного сечения определяется координатами
|
(5.1) |
здесь площади частей плоской фигуры:

т.к.
 .
.
Статические
моменты частей фигуры относительно
осей





Находим
координаты центра составной фигуры в
координатных осях
 ,
учитывая, что фигура
,
учитывая, что фигура
 исключается из фигуры
исключается из фигуры
 .
.


|
Рис. 5.2
3.
Для расчета осевых и центробежного
моментов составной фигуры относительно
центральных осей
 необходимо знать соответствующие
моменты составляющих частей относительно
этих осей:
необходимо знать соответствующие
моменты составляющих частей относительно
этих осей:
|
(5.2) |
При
расчете этих моментов воспользуемся
формулами перехода от одной системы
координатных осей к другой ей параллельной.
Наиболее простой вид эти формулы
принимают, когда одна из координатных
систем является центральной (см. рис.
5.3 , где оси
центральные , т.е.
 .
.
здесь
|
Рис. 5.3 |
- для фигуры


- для фигуры 2


- для фигуры 3


Теперь находим:
- для первой фигуры оси главные центральные, тогда




-
для второй фигуры оси
 главные центральные, тогда
главные центральные, тогда





-
для третьей фигуры
оси
 главные центральные, тогда
главные центральные, тогда



Применяя формулы (5.2), находим:


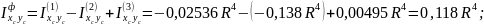
4. Наконец можно перейти к определению положения главных центральных осей плоской фигуры и вычислению осевых моментов относительно этих осей.
Оси
 - центральные оси фигуры, но они не
являются главными центральными, т.к.
- центральные оси фигуры, но они не
являются главными центральными, т.к.
 .
Положение главных центральных осей
.
Положение главных центральных осей
 определяется углом
определяется углом
 , для определения которого воспользуемся
зависимостью
, для определения которого воспользуемся
зависимостью
|
(5.4) |
Получаемые
из (5.4) два значения угла
отличаются на
 и определяют положение главных центральных
осей. как легко видеть, меньший из этих
углов по абсолютной величине не превышает
и определяют положение главных центральных
осей. как легко видеть, меньший из этих
углов по абсолютной величине не превышает
 .
Обычно пользуются меньшим углом
(положительным или отрицательным.
Проведенную под этим углом главную ось
обозначают буквой
.
Обычно пользуются меньшим углом
(положительным или отрицательным.
Проведенную под этим углом главную ось
обозначают буквой
 .
.
а) б) с) д) Рис. 5.4 |
В рассматриваемом примере


Из
возможных вариантов решения (см. рис.
5.4) принимаем вариант 5.4б). Оси
и
 показаны на рис. 5.2.
показаны на рис. 5.2.
Правильность
вычислений можно проверить , если
определить центробежный момент сечения
относительно осей
 .
Если угол
определен правильно, то центробежный
момент должен получиться равным нулю:
.
Если угол
определен правильно, то центробежный
момент должен получиться равным нулю:


что и требовалось доказать.
Теперь рассчитаем осевые моменты сечения относительно главных центральных осей:



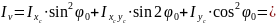


Легко
убедиться, что
 Это свойство осевых моментов сечения
относительно выбранных осей при их
повороте на угол
.
Это свойство осевых моментов сечения
относительно выбранных осей при их
повороте на угол
.
Значения осевых моментов сечения относительно главных центральных осей можно найти и по алгебраическим формулам, если известны моменты сечения относительно произвольных центральных осей :
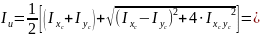




 .
.



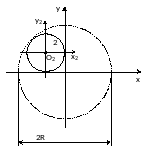









 координаты начала новых осей
координаты начала новых осей
 в старых осях. В рассматриваемой задаче
(рис. 5.2):
в старых осях. В рассматриваемой задаче
(рис. 5.2):

