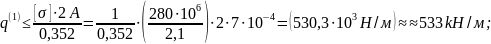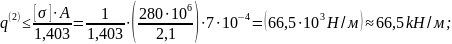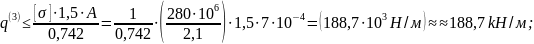- •Пример 2 Центральное растяжение - сжатие (стержневая система)
- •Решение
- •Пример 3 Кручение вала круглого поперечного сечения
- •Пример 4 Плоский изгиб
- •Задача 5 Геометрические характеристики плоского сечения
- •Решение
- •1. Главными центральными осями плоского сечения называют оси проходящие через центр сечения, относительно которых центробежный момент сечения равен нулю.
- •4. Наконец можно перейти к определению положения главных центральных осей плоской фигуры и вычислению осевых моментов относительно этих осей.
- •Задача №6
- •Решение
- •3. Необходимые для решения задачи перемещения определим, используя интеграл Мора:
- •Двутавры стальные горячекатаные сортамент гост 8239-89
- •7. Приведем, как пример, проверку условия прочности в сечении, где , (это сечение над опорой ):
Пример 1 Центральное растяжение - сжатие
Ступенчатый стержень нагружен тремя силами. Условия нагружения - центральное растяжение - сжатие.
Дано:
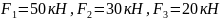 ;
;
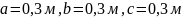 ;
;
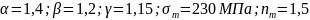 ;
;
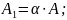
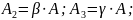
Необходимо:
определить реакцию связи;
определить продольное усилие на каждом участке вала и построить эпюру продольного усилия;
назначить площадь поперечных сечений стержня на каждом участке, удовлетворяя условию прочности, при стремлении минимизировать массу конструкции;
найти линейные перемещения характерных сечений стержня и построить эпюру перемещений.
Решение
1. Из условия уравновешенности системы сил, действующей на стержень, находим реакцию связи (рис.1.1)
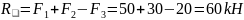 .
.
2.
Далее, используя метод сечений, определяем
продольное усилия на участках стержня
и строим эпюру продольного усилия
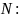
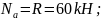
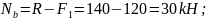
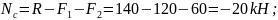
3.
Условие прочности при центральном
растяжении - сжатии должно выполняться
и на участке
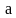 ,
и на участке
,
и на участке
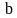 ,
и на участке
,
и на участке
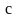 :
:
|
(1.1) |
Используя
условия (1.1) находим минимальное значение
параметра
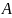 ,
который определяет связанные конструктивно
площади сечений
,
который определяет связанные конструктивно
площади сечений
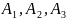 :
:
из условия прочности на участке "a"
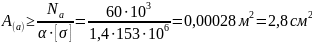 ;
;
из условия прочности на участке "a"
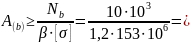 5,45
5,45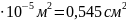 ;
;
из условия прочности на участке "a"
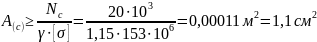 ;
;
Принимаем
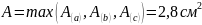 .
.
Тогда на участках стержня площади сечений будут такими:
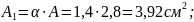
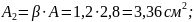
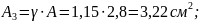
|
Рис 1.1
3. Определим удлинение каждого участка стержня
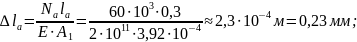
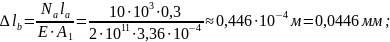
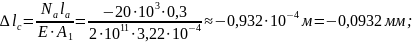
Рассчитаем перемещения характерных сечений стержня
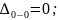
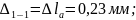
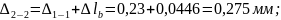
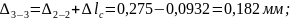
Строим эпюру линейных перемещений сечений стержня (см. рис.1.1).
Пример 2 Центральное растяжение - сжатие (стержневая система)
Абсолютно
твердое тело BCD
закреплено в плоскости тремя стержнями,
имеющими различную площадь поперечного
сечения
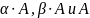 .
.
Необходимо
определить максимально допустимое
значение внешней нагрузки
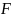 или
или
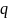 при
выполнении условий прочности для всех
прикрепляющих стержней.
при
выполнении условий прочности для всех
прикрепляющих стержней.
Геометрические размеры и допускаемые напряжения известны.
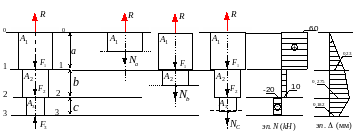
Рис. 2.1 |
|
Решение
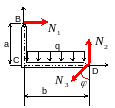
Очевидно, что усилия в прикрепляющих стержнях зависят от интенсивности распределенной нагрузки и геометрических параметров конструкции. Понимая это, можно записать систему неравенств (условий прочности), которым должно удовлетворять разыскиваемое решение:
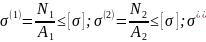
(2.1)
Наложенные на тело
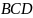 связи, стержни 1, 2, 3, заменяем реакциями
связей
связи, стержни 1, 2, 3, заменяем реакциями
связей
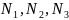 (рис. 2.1) и из условий уравновешенности
системы сил {
(рис. 2.1) и из условий уравновешенности
системы сил {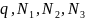 }
определяем усилия
}
определяем усилия
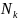 через
.
через
.
Рис. 2.1 |
здесь
|
Решение системы уравнений (2.2) дает результат:
|
|
|
(2.4) |
|
|
Теперь из условий (2.1) получаем допустимые значения :
]; - из условия прочности для стержня 2:
- из условия прочности для стержня 3:
|
|
Условия прочности для всех прикрепляющих стержней будут выполнены, если
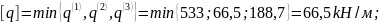
Проверим решение задачи.
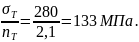 Если
Если
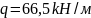 ,
то:
,
то:
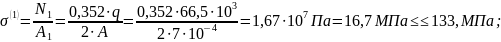
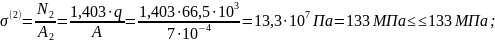
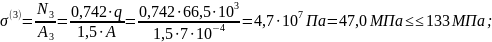
Условие прочности для прикрепляющих стержней выполняется.
Пример 3 Кручение вала круглого поперечного сечения
Ступенчатый брус круглого поперечного сечения нагружен внешними моментами, приложенными в трех сечениях.
Необходимо:
-
построить эпюру крутящего момента
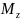 ;
;
- из условия прочности определить безопасные значения диаметров на каждом участке бруса, принимая во внимание их взаимозависимость:
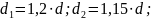 ;
;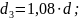 допускаемое напряжение принять
допускаемое напряжение принять
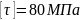 .
.
- построить эпюру углов поворота сечений относительно заделки;
- проверить выполнение условия жесткости на всех участках вала.
Дано:
а=0,6
м; b=0,4
м; c=0,3
м;
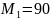 Н·м;
Н·м;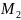 =20
Н·м;
=20
Н·м;
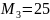 Н·м;
Н·м;
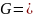 0,7
0,7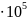 МПа;
МПа;
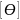 =1,3град/м.
=1,3град/м.
Решение
1.
Определим реакцию связи - момент в
заделке
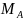 .
.
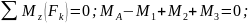
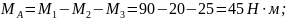
2. Используя метод сечений определим крутящий момент в сечениях на участках вала (см. рис. 3.1):
уч
"a"
;
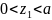
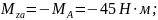
уч
"b"
;
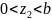
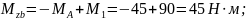
уч
"c"
;
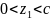
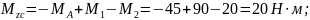
3.
Строим эпюру крутящего момента и из
условия прочности на каждом участке
стержня определяем безопасное значение
параметра
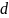 :
:
- условие прочности сечения
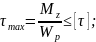
где
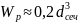 -полярный момент сечения;
-полярный момент сечения;
- из условия прочности на участке "a"
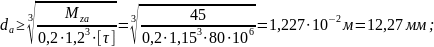
- из условия прочности на участке "b"
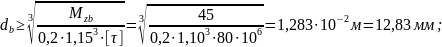
- из условия прочности на участке "c"
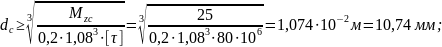
Значение
параметра
,
при котором удовлетворяется условие
прочности на всех участках вала
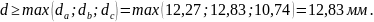
Принимаем
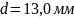 .
Тогда участки стержня должны иметь
следующие диаметры:
.
Тогда участки стержня должны иметь
следующие диаметры:
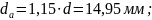
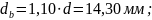
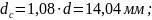
4. Теперь построим эпюру углов поворота сечений вала относительно заделки и проверим выполнение условия жесткости по погонному углу поворота.
Взаимный
угол поворота двух сечений вала, отстоящих
друг от друга на расстоянии
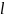 при
при
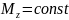 определяется по формуле
определяется по формуле
Определяем:
- угол поворота сечения относительно сечения
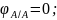
- угол поворота сечения 1 относительно сечения
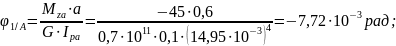
- угол поворота сечения 2 относительно сечения 1
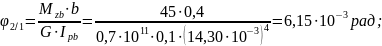
- угол поворота сечения 3 относительно сечения 2
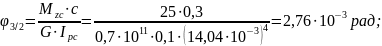
- угол поворота сечения 2 относительно сечения
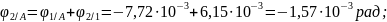
- угол поворота сечения 3 относительно сечения
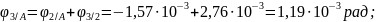
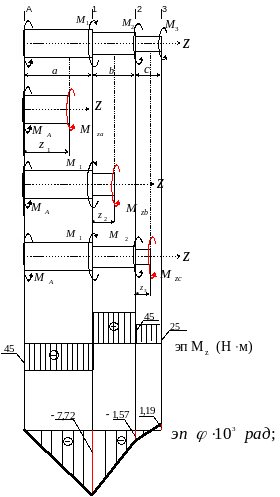
Строим
эпюру углов поворота сечений вала
относительно заделки (сечение
)
- эпюра
 на рис. 3.1.
на рис. 3.1.
5. Проверим выполнение условия жесткости по погонному углу поворота для рассматриваемого вала. Условие жесткости имеет вид
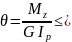 ];
];
Допускаемое значение погонного угла поворота в радианах на метр равно
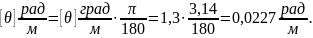 ]
]
Проверяем условие жесткости на каждом участке вала:
- на участке "a"
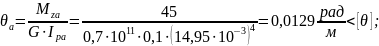
Рис. 3.1 |
|
- на участке "b"
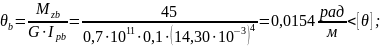
- на участке "c"
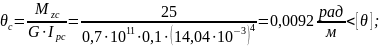
Полученные результаты позволяют сделать вывод: спроектированный по условию прочности вал удовлетворяет и условию жесткости.

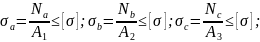
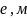
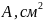
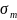 ,
МПа
,
МПа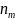
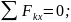
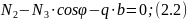
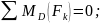
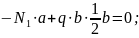
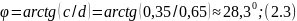
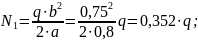
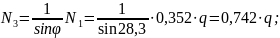
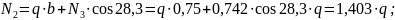
 ];
- из условия прочности для стержня 1:
];
- из условия прочности для стержня 1: