2.5. Задачи для самостоятельной работы
Задача
1. С помощью
линий уровня исследовать поведение
функции и построить ее график.
1.
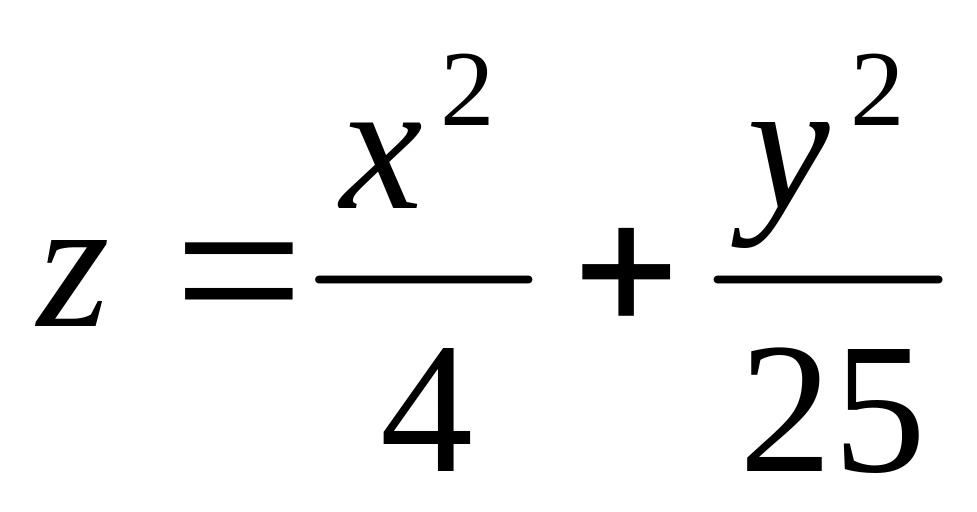 . 2.
. 2.
 . 3.
. 3.
 .
.
4.
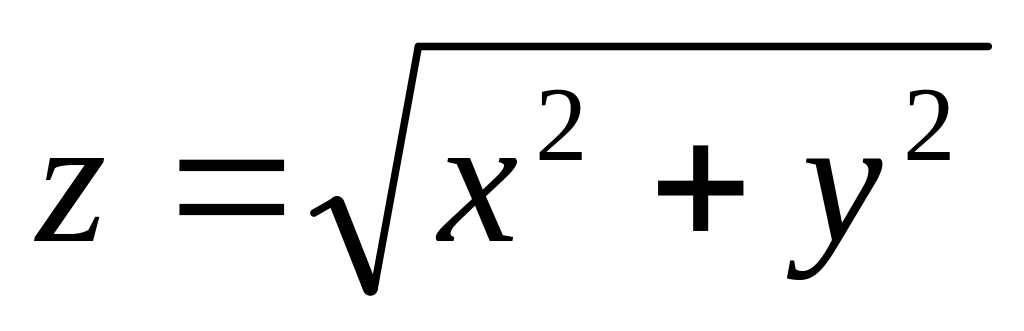 . 5.
. 5.
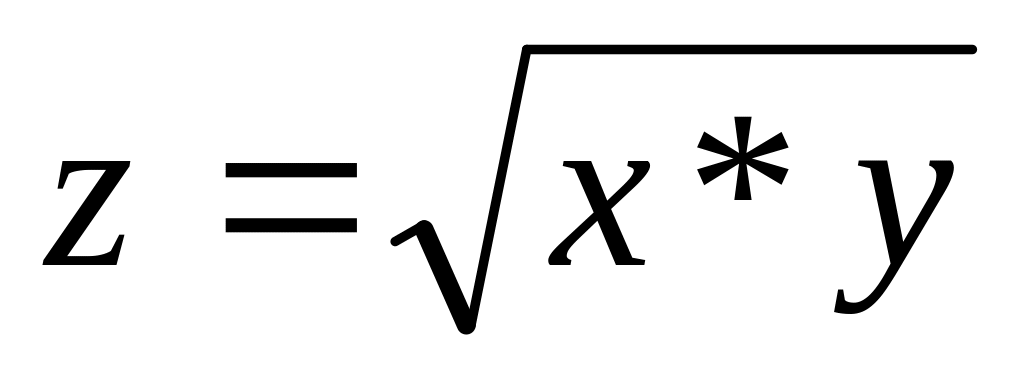 . 6.
. 6.
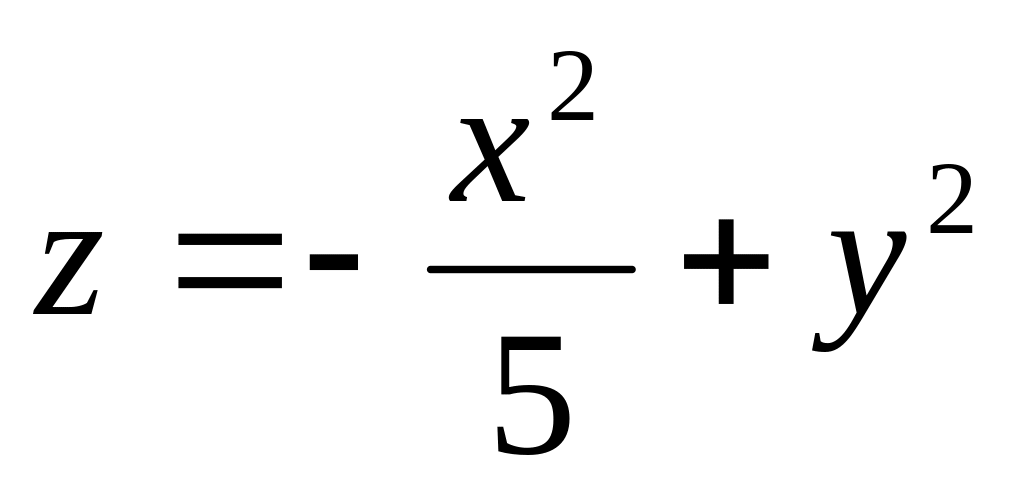 .
.
7.
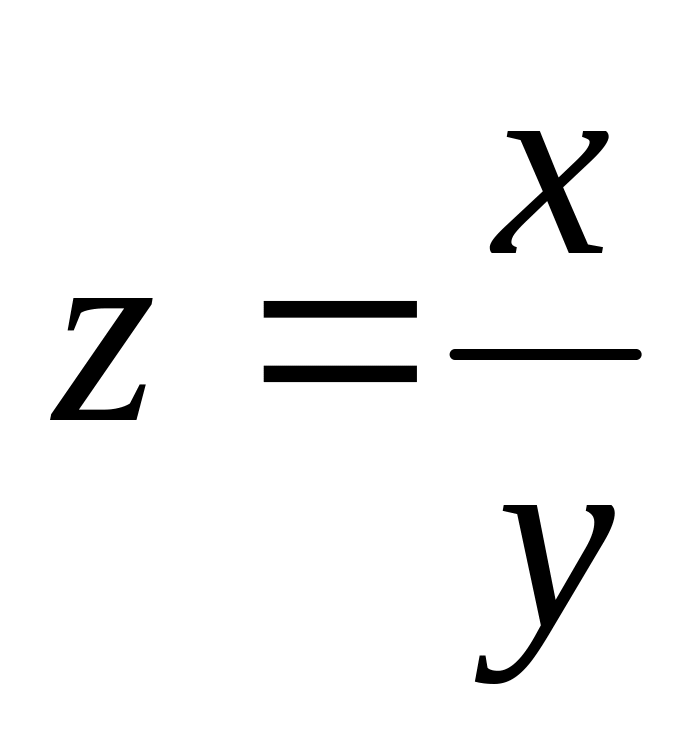 . 8.
. 8.
 . 9.
. 9.
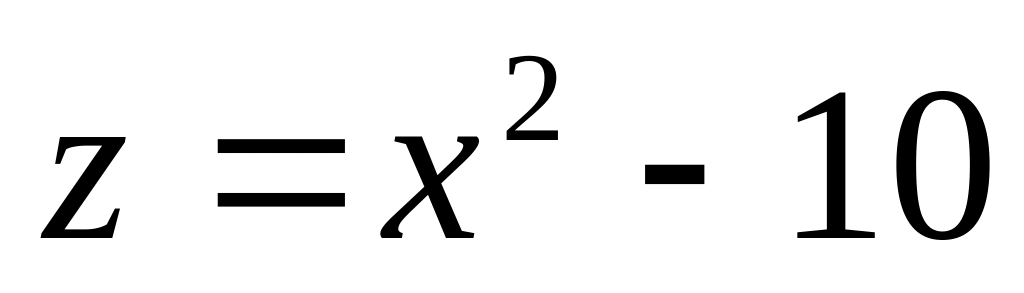 .
.
10.
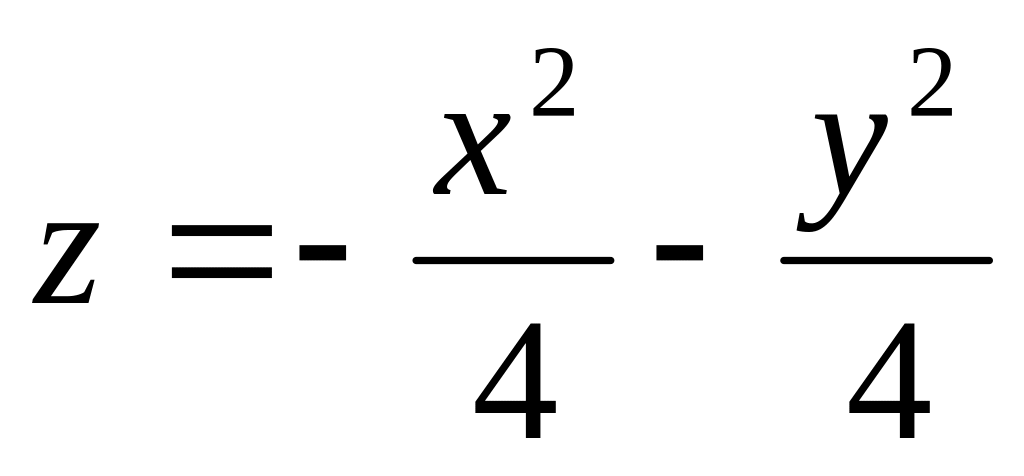 . 11.
. 11.
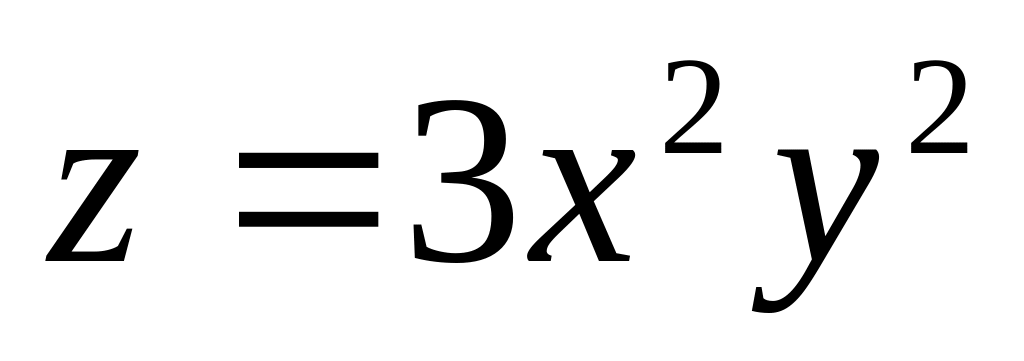 . 12.
. 12.
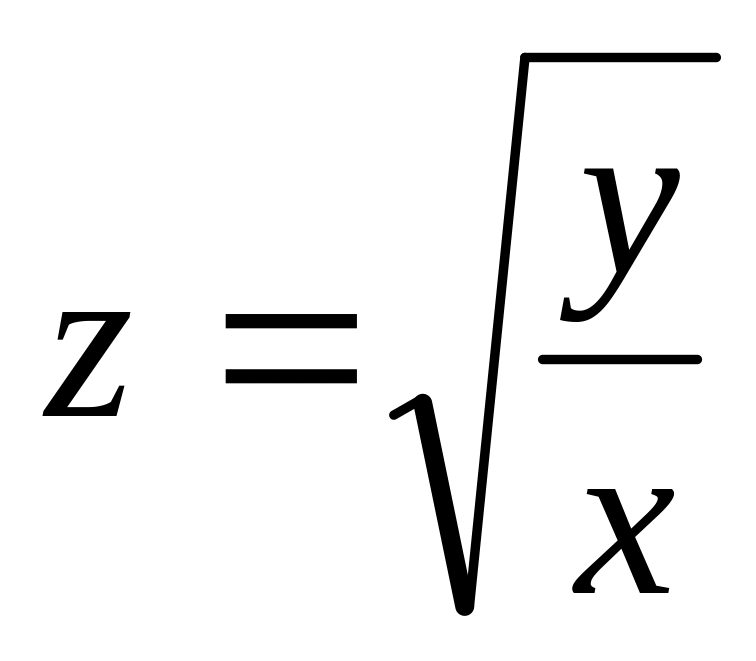 .
.
13.
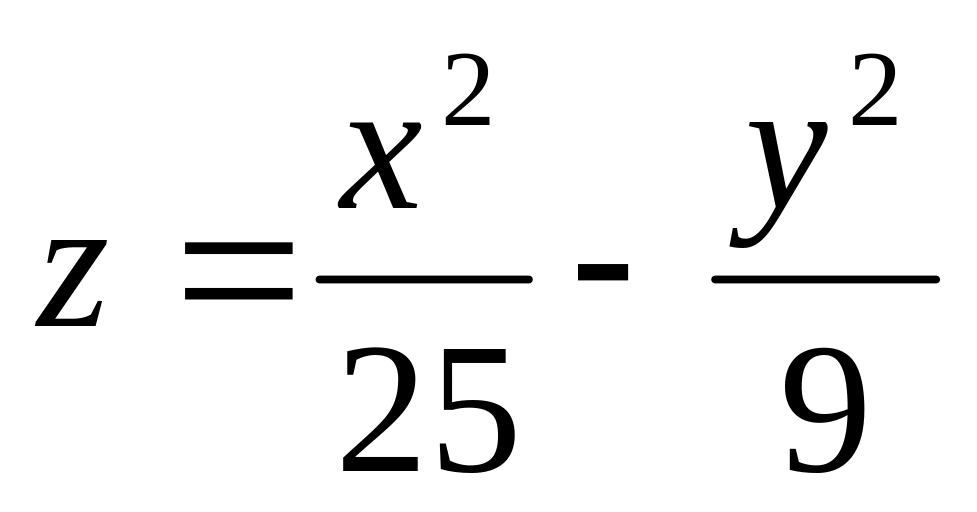 . 14.
. 14.
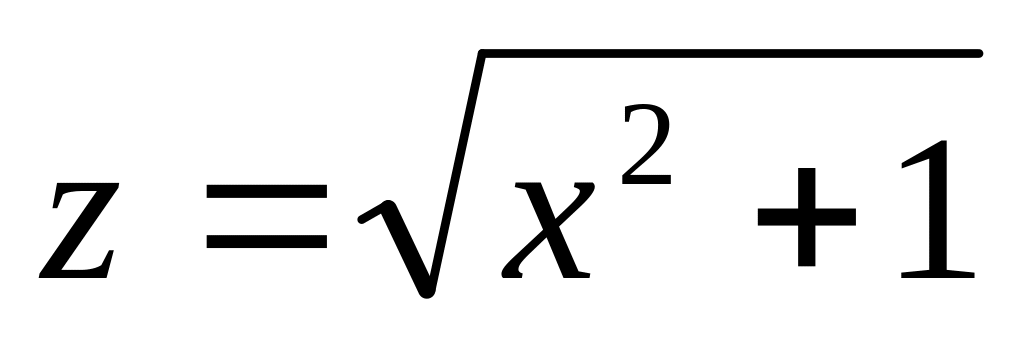 . 15.
. 15.
 .
.
Задача
2. Для указанной
функции найти полные дифференциалы
первого и второго порядка в точке
 .
.
1.
 ,
Р(1,2,3); 2.
,
Р(1,2,3); 2.
 ,
Р(1,-1,2);
,
Р(1,-1,2);
3.
 ,
Р(2,3,4); 4.
,
Р(2,3,4); 4. ,
Р(1,1,1);
,
Р(1,1,1);
5.
 ,
Р(1,2,2); 6.
,
Р(1,2,2); 6.
 ,
Р(3,1,2);
,
Р(3,1,2);
7.
 ,
Р(1,1,2); 8.
,
Р(1,1,2); 8.
 ,
Р(1,2,3);
,
Р(1,2,3);
9.
 ,
Р(1,-1,0); 10.
,
Р(1,-1,0); 10.
 ,
,
 ;
;
11.
 ,
Р(1,4,2); 12.
,
Р(1,4,2); 12.
 ,
Р(3,3,1);
,
Р(3,3,1);
13.
 ,
Р(1,3,4); 14.
,
Р(1,3,4); 14.
 ,
,
 ;
;
15.
,
Р(2,2,3).
Задача
3. Для указанной
функции найти производную по направлению
вектора
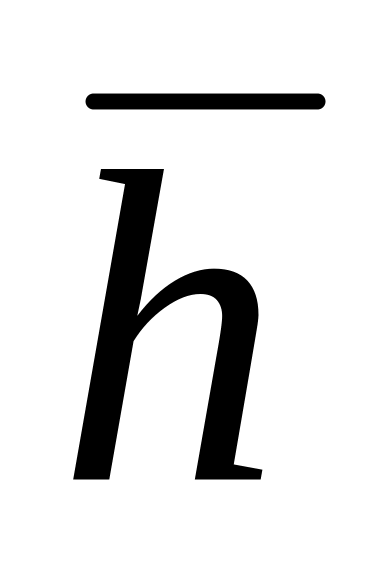 в точке
в точке
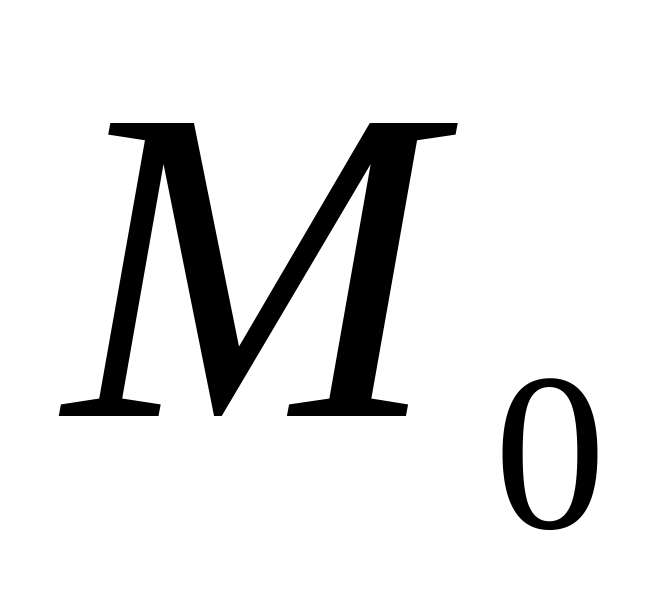 .
.
1.
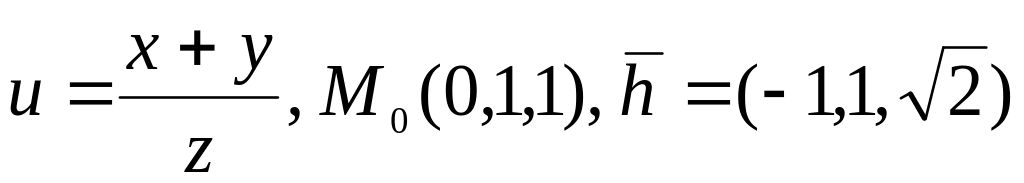 .
.
2.
 .
.
3.
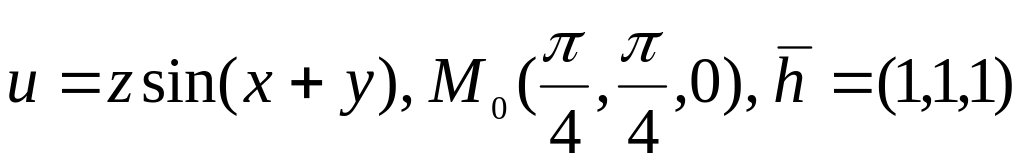 .
.
4.
 .
.
5.
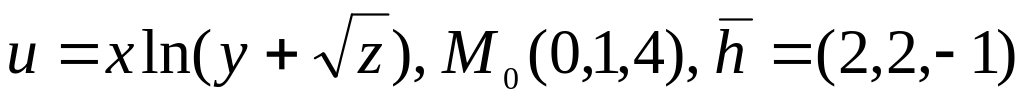 .
.
6.
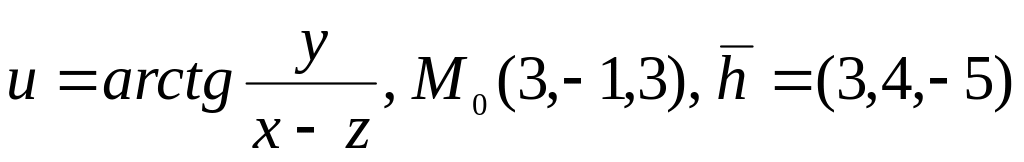 .
.
7.
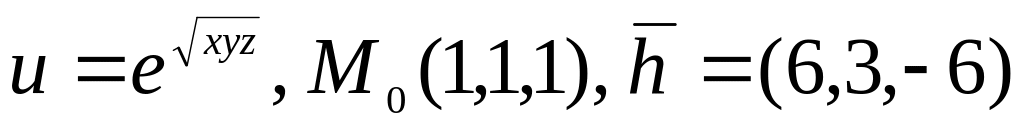 .
.
8.
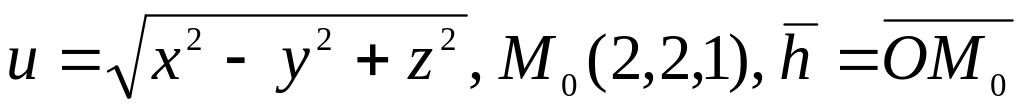 .
.
9.
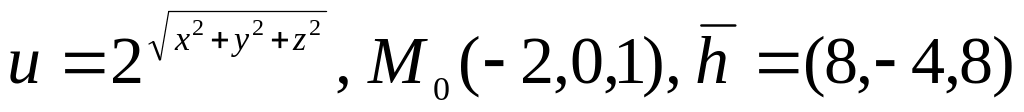 .
.
10.
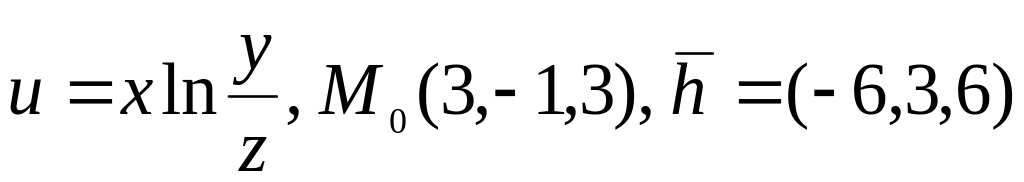 .
.
11.
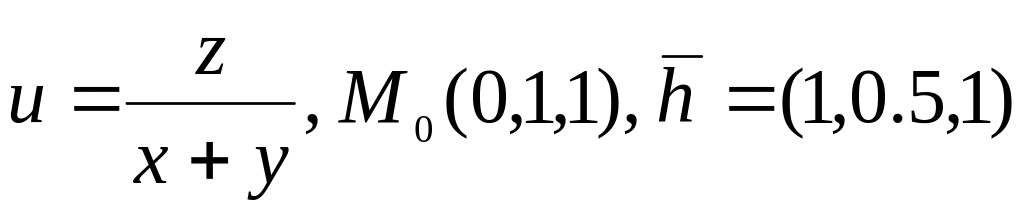 .
.
12.
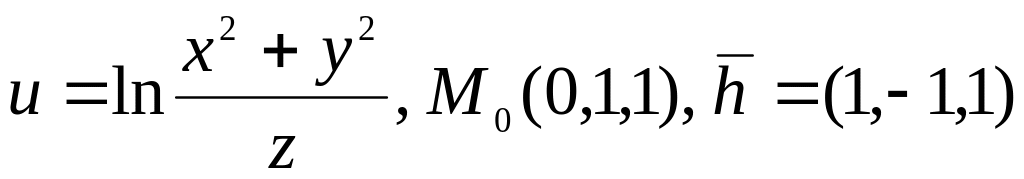 .
.
13.
.
14.
 .
.
15.
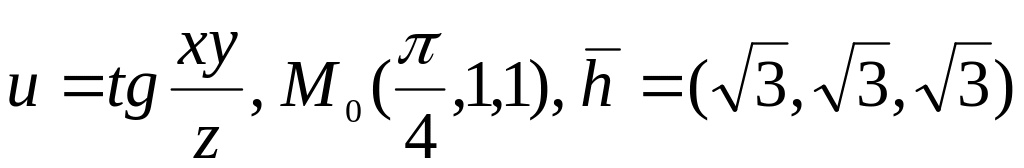 .
.
Задача
4. Найти
критические точки функции и исследовать
их характер.
1.
 ; 2.
; 2.
 ;
;
3.
 ; 4.
; 4.
 ;
;
5. ; 6.
; 6.
 ;
;
7.
 ; 8.
; 8.
 ;
;
9.
 ; 10.
; 10.
 ;
;
11.
 ; 12.
; 12.
 ;
;
13.
 ; 14.
; 14.
 ;
;
15.
 .
.
Содержание отчета по работе
1.
Исходное задание и цель работы.
2.
Распечатка контрольного примера и
результатов машинного расчета.
4.5
Выводы по работе.
Контрольные вопросы


 ;
; ;
;