
Упражнения
7.1. Доказать свойства:
наибольший общий делитель многочленов равен их общему делителю наибольшей степени;
наименьшее общее кратное многочленов равно их общему кратному наименьшей степени;
 для любого
;
для любого
; тогда и только
тогда, когда
тогда и только
тогда, когда
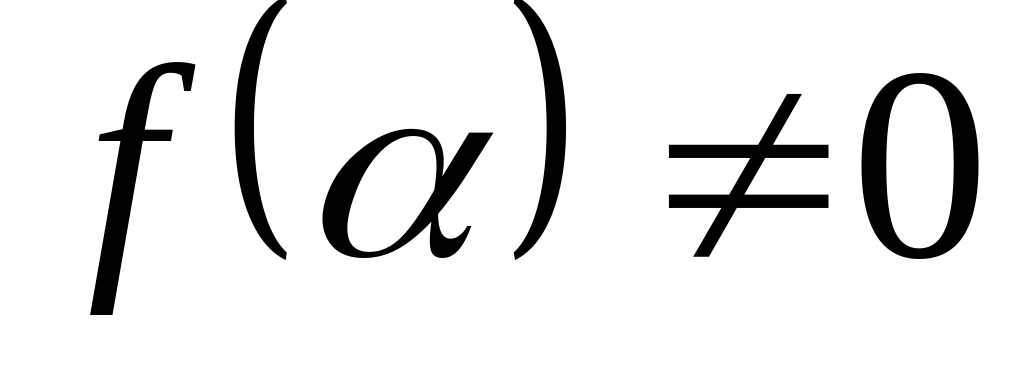 ;
;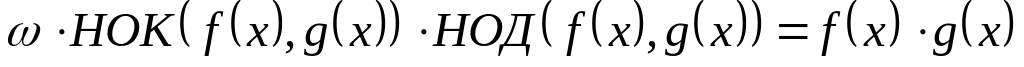 ,
где
-
произведение коэффициентов при старших
степенях многочленов
и
;
,
где
-
произведение коэффициентов при старших
степенях многочленов
и
;если
 ,
то
,
то
 ;
;пусть
 -
конечное множество чисел. Многочлен
-
конечное множество чисел. Многочлен
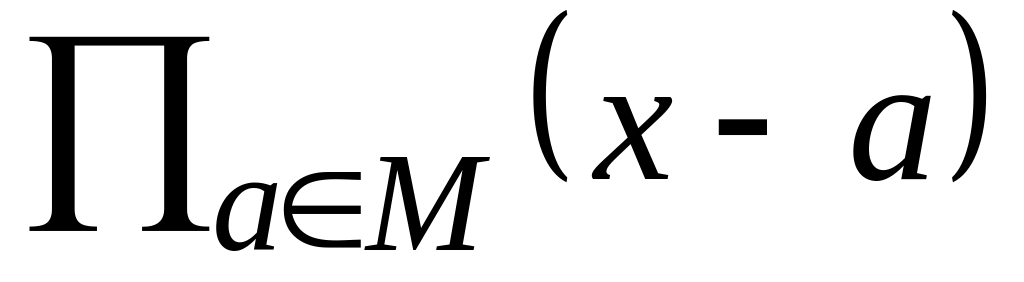 взаимно простой с
тогда и только тогда, когда
взаимно простой с
тогда и только тогда, когда
 для всех
для всех
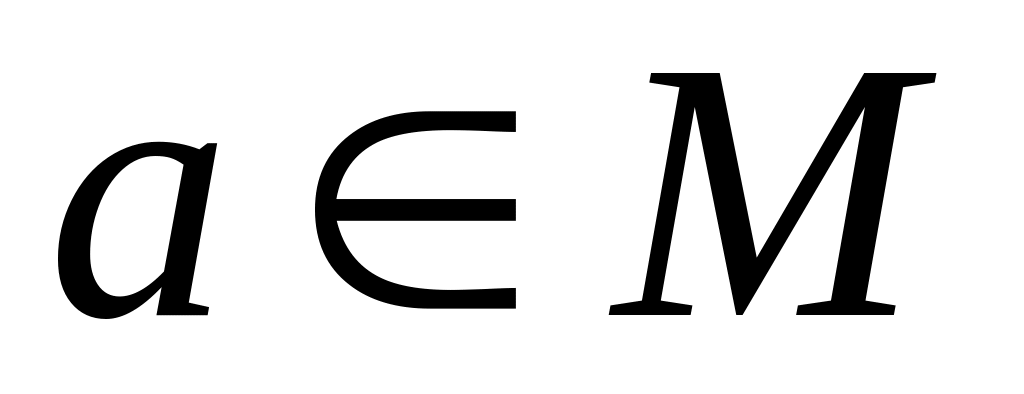 ;
;если , то
 ;
;если и
 ,
то
,
то
 ;
;если , то и ;
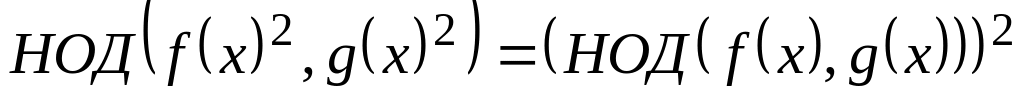 .
.
7.2. Найти наибольший общий делитель многочленов алгоритмом Евклида (если поле не указано, то подразумевается поле рациональных чисел):
 и
и
 ;
; и
и
 ;
; и
и
 ;
;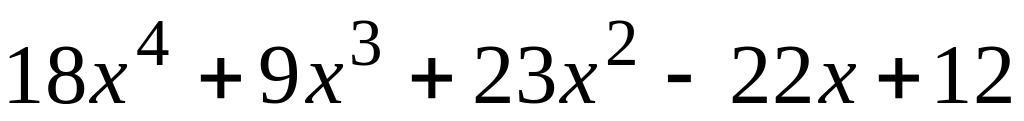 и
и
 ;
; и
и
 ;
; и
и
 ;
; и
и
 над
;
над
; и
и
 над
.
над
.
7.3. Найти наибольший общий делитель многочленов над полем рациональных чисел:
 и
и
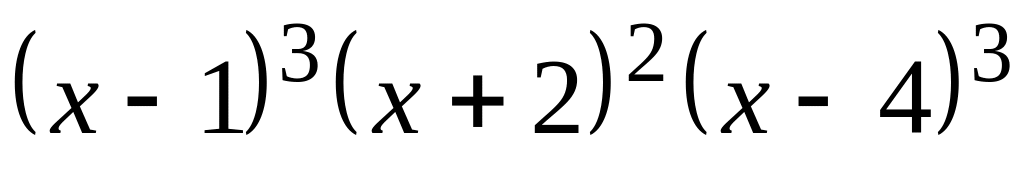
 ;
; и
и
 ;
;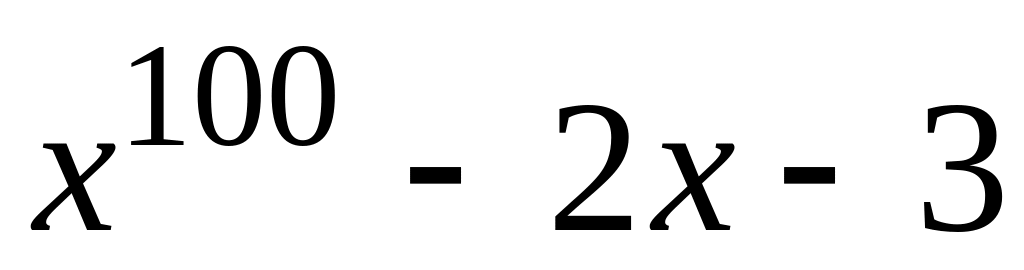 и
и
 ;
;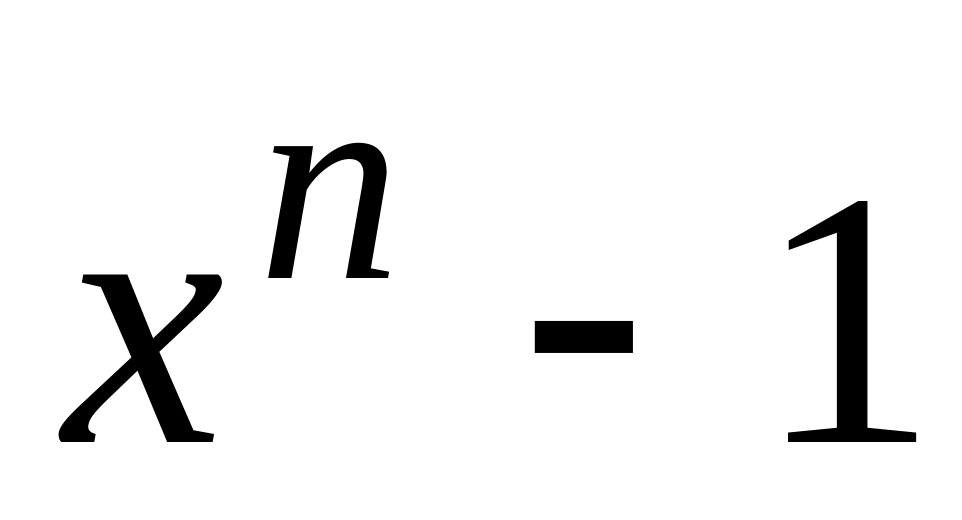 и
и
 .
.
7.4. Найти наименьшее общее кратное многочленов над полем рациональных чисел:
и ;
 и
и
 ;
; и
и
 .
.
7.5*.
Для многочленов с рациональными
коэффициентами
![]() и
и
![]() найти наибольший общий делитель и
коэффициенты Безу расширенным алгоритмом
Евклида.
найти наибольший общий делитель и
коэффициенты Безу расширенным алгоритмом
Евклида.
7.6. Расширенным алгоритмом Евклида найти наибольший общий делитель многочленов и коэффициенты Безу:
и ;
 и
и
 ;
; и
и
 ;
; и
и
 ;
;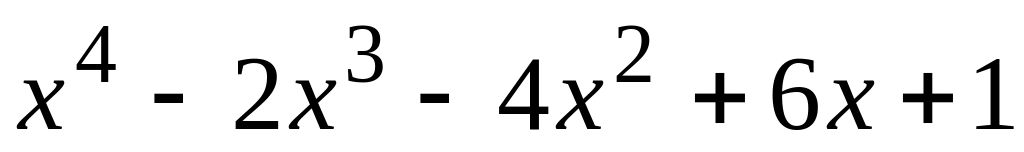 и
и
 ;
; и
и
 ;
;и
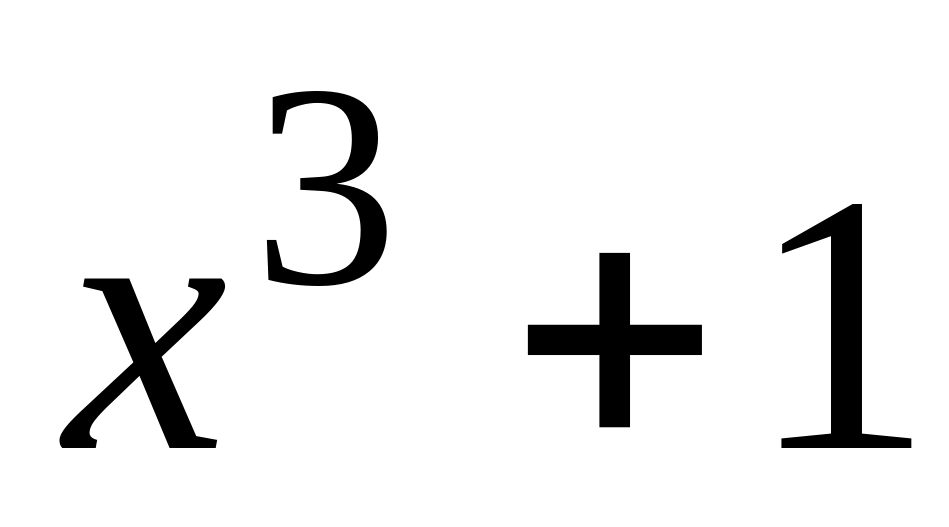 над
;
над
; и
и
 над
.
над
.
7.7*. Методом
неопределенных коэффициентов найти
коэффициенты Безу для взаимно простых
многочленов
![]() и
и
![]() .
.
7.8*. Найти
многочлены
![]() и
и
![]() минимальной степени, удовлетворяющие
равенству
минимальной степени, удовлетворяющие
равенству
![]() .
.
7.9. Найти коэффициенты Безу методом неопределенных коэффициентов:
и ;
и
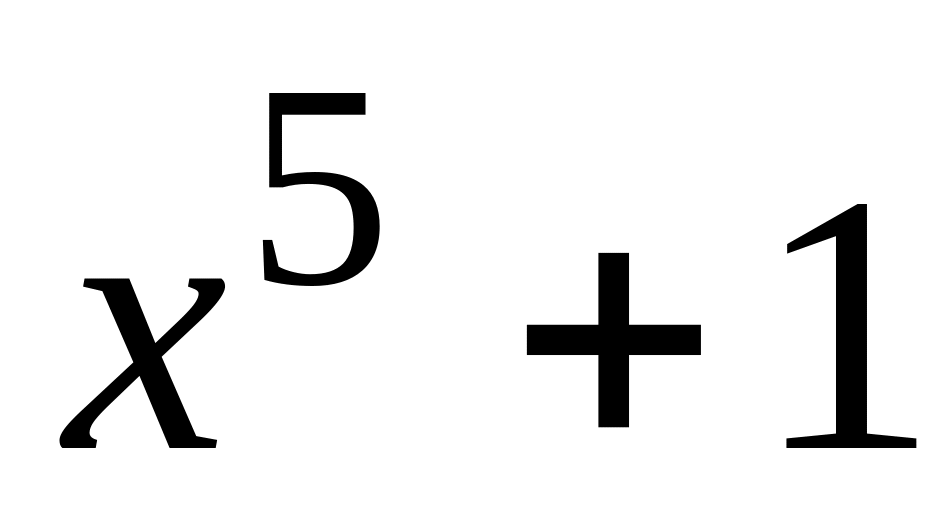 ;
;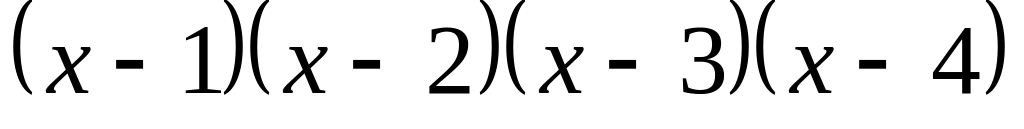 и
и
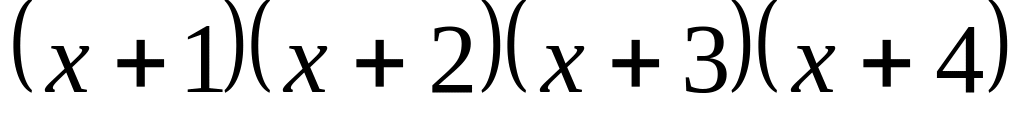
 и
и
 над
;
над
; и
и
 над
.
над
.
7.10*.
Освободиться от иррациональности в
знаменателе
![]() .
.
7.11. Освободиться от иррациональности в знаменателе:
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
7.12*.
Пусть
![]() .
Доказать, что найдутся такие многочлены
.
Доказать, что найдутся такие многочлены
![]() и
,
для которых
и
,
для которых
![]() .
.
7.13. Представить в виде суммы дробей:
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
8. Интерполяционный многочлен
Задача построения многочлена наименьшей степени, который в заданных точках, называемыми узлами интерполяции, принимает заданные значения, называется задачей интерполяции. Решение задачи интерполяции называют интерполяционным многочленом.
Пусть
![]() (
(![]() )
– узлы интерполяции, а
)
– узлы интерполяции, а
![]() - значения. Положим
- значения. Положим
![]() ,
где
,
где
![]() .
Очевидно, что
.
Очевидно, что
![]() ,
при
,
при
![]() ,
и
,
и
![]() .
Многочлен
.
Многочлен
![]() называют интерполяционным
многочленом в форме Лагранжа.
называют интерполяционным
многочленом в форме Лагранжа.
Разностью
первого порядка
многочлена
в узлах
![]() назовем
назовем
![]() .
Индуктивно определим разность
порядка
многочлена
в узлах
.
Индуктивно определим разность
порядка
многочлена
в узлах
![]() через разности
через разности
![]() порядка по формуле:
порядка по формуле:
![]() .
Разность порядка
выражается через значения многочлена
в узлах
.
Разность порядка
выражается через значения многочлена
в узлах
 ,
и, следовательно, разность не зависит
от порядка расположения ее аргументов.
,
и, следовательно, разность не зависит
от порядка расположения ее аргументов.
Если степень
многочлена
равна
,
то разность
![]() порядка
есть многочлен степени
порядка
есть многочлен степени
![]() при
при
![]() .
Если
.
Если
![]() ,
то разность порядка
равна нулю. Из определения разности
порядка
выводим равенство, позволяющее выразить
многочлен через соответствующие разности
,
то разность порядка
равна нулю. Из определения разности
порядка
выводим равенство, позволяющее выразить
многочлен через соответствующие разности
![]() .
При решении задачи интерполяции
.
При решении задачи интерполяции
![]() ,
и, значит, получаем представление
интерполяционного
многочлена в
форме
Ньютона
,
и, значит, получаем представление
интерполяционного
многочлена в
форме
Ньютона
![]() .
.
