6 Определение качества процесса регулирования
Задача
Определить качество процесса регулирования
для автоматической системы, описываемой
передаточной функцией
.
Решение
Передаточная функция замкнутой системы будет равна
.
Корни характеристического полинома
равны
,
.
следовательно, степень устойчивости
.
Можно оценить время регулирования
.
Зная корни характеристического полинома, можно определить колебательность переходного процесса
.
количество
колебаний
за время переходного процесса
не превышает
.
период колебаний переходного процесса равен
.
Время максимального перерегулирования определяется по формуле
.
Величина максимального перерегулирования
оценивается по формуле
.
Индивидуальные условия к задачам
Таблица 1 – Исходные данные к задачам раздела 1 и 2
Вариант |
Передаточная функция элемента для
нахождения весовой
|
Передаточная функция элемента для
нахождения переходной
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|
|
31 |
|
|
32 |
|
|
33 |
|
|
34 |
|
|
35 |
|
|
функции
функции
Исходные данные к задаче раздела 3
Структурные схемы линейной САУ
1.
2.
3.
4.
5.
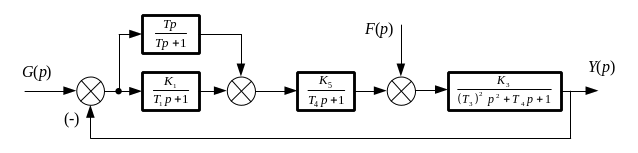
6.
Таблица 2 - Параметры структурной схемы САУ
Вариант |
Параметр |
|||||||||||
K |
K1 |
K2 |
K3 |
K4 |
K5 |
T |
T1 |
T2 |
T3 |
T4 |
T5 |
|
1 |
0,1 |
10 |
20 |
1 |
2 |
1 |
0,15 |
0,012 |
0,07 |
0,1 |
0,25 |
0,01 |
2 |
0,2 |
9 |
6 |
2,8 |
0,3 |
1 |
0,16 |
0,017 |
0,06 |
0,2 |
0,3 |
0,02 |
3 |
0,3 |
4 |
30 |
1 |
8 |
1,5 |
0,17 |
0,016 |
0,05 |
0,3 |
0,18 |
0,03 |
4 |
0,4 |
20 |
6 |
1,5 |
6 |
1,6 |
0,18 |
0,4 |
0,4 |
0,4 |
0,1 |
0,04 |
5 |
0,5 |
7 |
10 |
2,1 |
0,2 |
0,8 |
0,08 |
0,01 |
0,3 |
0,5 |
0,3 |
0,05 |
6 |
0,05 |
6 |
6 |
6 |
0,5 |
0,2 |
0,09 |
0,02 |
0,2 |
0,6 |
0,47 |
0,06 |
7 |
0,06 |
7,8 |
2,6 |
5 |
3 |
1,4 |
0,2 |
0,03 |
0,1 |
0,7 |
0,3 |
0,07 |
8 |
0,07 |
8,5 |
8,5 |
2 |
2 |
2,3 |
0,25 |
0,04 |
0,016 |
0,8 |
0,16 |
0,08 |
9 |
0,08 |
10 |
6 |
3 |
9 |
2 |
0,3 |
0,05 |
0,015 |
0,9 |
1,0 |
0,09 |
10 |
0,09 |
10 |
1,5 |
6 |
0,6 |
0,15 |
0,01 |
0,06 |
0,017 |
0,75 |
0,2 |
0,1 |
11 |
0,7 |
5 |
5 |
5 |
0,9 |
4,2 |
0,35 |
0,07 |
0,018 |
0,45 |
0,15 |
0,12 |
12 |
0,6 |
2 |
4 |
20 |
1,5 |
0,5 |
0,02 |
0,08 |
0,012 |
0,25 |
0,2 |
0,15 |
13 |
0,04 |
2,9 |
8 |
7 |
2,6 |
0,4 |
0,19 |
0,09 |
0,5 |
0,15 |
0,5 |
0,16 |
14 |
0,03 |
2 |
12 |
8 |
2,1 |
0,3 |
0,4 |
0,014 |
0,04 |
0,15 |
0,35 |
0,17 |
15 |
0,8 |
12 |
1,7 |
10 |
3,3 |
0,004 |
0,015 |
0,03 |
0,18 |
0,25 |
0,25 |
0,18 |
16 |
0,9 |
15 |
1,1 |
12 |
10 |
2,5 |
0,5 |
0,025 |
0,08 |
0,13 |
0,18 |
0,19 |
17 |
0,15 |
14 |
2,3 |
5,5 |
8 |
4,5 |
0,55 |
0,035 |
0,09 |
0,05 |
0,1 |
0,2 |
18 |
0,25 |
13 |
2,4 |
6,5 |
0,2 |
1,8 |
0,03 |
0,045 |
0,095 |
0,06 |
0,15 |
0,25 |
19 |
0,35 |
12 |
3,3 |
4 |
0,3 |
1,3 |
0,04 |
0,055 |
0,25 |
0,04 |
0,07 |
0,3 |
20 |
0,45 |
5,5 |
3,2 |
9 |
0,8 |
1,2 |
0,08 |
0,065 |
0,28 |
0,13 |
0,2 |
0,35 |
21 |
0,1 |
10 |
20 |
1 |
1,5 |
1 |
0,15 |
0,012 |
0,07 |
0,1 |
0,25 |
0,01 |
22 |
0,5 |
7 |
10 |
2,1 |
0,2 |
0,8 |
0,08 |
0,01 |
0,3 |
0,5 |
0,3 |
0,05 |
23 |
0,15 |
14 |
2,3 |
5,5 |
8 |
4,5 |
0,55 |
0,035 |
0,09 |
0,05 |
0,1 |
0,2 |
24 |
0,8 |
12 |
1,7 |
10 |
3,3 |
0,004 |
0,015 |
0,03 |
0,18 |
0,25 |
0,25 |
0,18 |
25 |
0,2 |
9 |
6 |
2,8 |
0,3 |
1 |
0,16 |
0,017 |
0,06 |
0,2 |
0,3 |
0,02 |
26 |
0,7 |
5 |
5 |
5 |
0,9 |
4,2 |
0,35 |
0,07 |
0,018 |
0,45 |
0,15 |
0,12 |
27 |
0,04 |
2,9 |
8 |
7 |
2,6 |
0,4 |
0,19 |
0,09 |
0,5 |
0,15 |
0,5 |
0,16 |
28 |
0,3 |
4 |
30 |
1 |
8 |
1,5 |
0,17 |
0,016 |
0,05 |
0,3 |
0,18 |
0,03 |
29 |
0,6 |
2 |
4 |
20 |
1,5 |
0,5 |
0,02 |
0,08 |
0,012 |
0,25 |
0,2 |
0,15 |
30 |
0,35 |
12 |
3,3 |
4 |
0,3 |
1,3 |
0,04 |
0,055 |
0,25 |
0,04 |
0,07 |
0,3 |
31 |
0,5 |
7 |
10 |
2,1 |
0,2 |
0,8 |
0,08 |
0,01 |
0,3 |
0,5 |
0,3 |
0,05 |
32 |
0,03 |
2 |
12 |
8 |
2,1 |
0,3 |
0,4 |
0,014 |
0,04 |
0,15 |
0,35 |
0,17 |
33 |
0,05 |
6 |
6 |
6 |
0,5 |
0,2 |
0,09 |
0,02 |
0,2 |
0,6 |
0,47 |
0,06 |
34 |
0,03 |
2 |
12 |
8 |
2,1 |
0,3 |
0,4 |
0,014 |
0,04 |
0,15 |
0,35 |
0,17 |
35 |
0,45 |
5,5 |
3,2 |
9 |
0,8 |
1,2 |
0,08 |
0,065 |
0,28 |
0,13 |
0,2 |
0,35 |
Приложение
Таблица 3 – Фрагмент таблицы преобразования Лапласа
№ п\п |
Оригинал функции
|
Изображение функции по Лапсаллсу
|
1 |
|
1 |
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
Основные свойства преобразования Лапласа
1. Теорема сложения
Изображение суммы нескольких функций равно сумме изображений этих функций
и наоборот
2. Изображение функции, умноженной на константу
Константа выносится за знак изображения
,
и наоборот
.
3. Изображение производной функции
При нулевых
начальных условиях изображение от
производной функции n-го
порядка равно произведению переменной
на изображение исходной функции
,
и наоборот
.
При ненулевых начальных условиях преобразование имеет следующий вид
,
где
- значение функции
при
.
4. Изображение от функции с запаздыванием
Изображение от функции с
запаздыванием τ равно произведению
множителя
на изображение исходной функции
,
и наоборот
.
5. Теорема Лапласа о начальном значении
.
6. Теорема Лапласа о конечном значении
.