ФГБОУ ВПО «Мордовский государственный университет им. Н. П. Огарева»

Институт механики и энергетики

Кафедра электрификации и автоматизации производства

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ

КОНТРОЛЬНОЙ РАБОТЫ

по дисциплине «Теория автоматического управления»

Саранск 2015

Содержание

1 Определение весовой функции ω(t)……………………………………………3

2 Определение переходной функции h(t)……………………………………….4

3 Структурные преобразования…………………………………………………5

4 Определение устойчивости системы управления алгебраическим критерием………………………………………………………………………….8

4.1 Определение устойчивости системы управления критерием Гурвица….8

4.2 Определение устойчивости системы управления критерием Рауса……..9

5 Определение устойчивости системы управления частотным критерием….9

5.1 Определение устойчивости системы управления критерием Михайлова..9

5.2 Определение устойчивости системы управления критерием Найквиста..10

6 Определение качества процесса регулирования……………………………12

Индивидуальные условия к задачам…………………………………………..13

Приложение………………………………………………………………………19

1 Определение весовой функции ω(t)

Задача

Модель элемента задана в виде передаточной функции . Требуется построить график весовой функции данного элемента.

Решение

Весовая функция звена есть его реакция на дельта-функцию.

.

Чтобы выполнить обратное преобразование Лапласа, воспользуемся таблицей преобразований (см. Приложение 1). В таблице имеется выражение, которое совпадает по структуре с выражением в фигурных скобках

.

Приведем выражение в фигурных скобках к табличному виду, для этого необходимо применить основные теоремы Лапласа (Приложение 1), в данном случае теорему линейности, согласно которой все константы могут быть вынесены за знак обратного преобразования Лапласа.

Получили выражение в фигурных скобках, в точности соответствующее табличному, где .

Тогда .

Задаваясь значениями t от 0 до ∞, можно получить график весовой функции. Однако даже при использовании вычислительной техники такой процесс является утомительным и зачастую так и не приводит к нужному результату. Поэтому следует вначале рассчитать начальное и конечное значения функции по предельным теоремам Лапласа (Приложение 1).

Найдем начальное значение весовой функции согласно

.

Разделим каждое слагаемое числителя и знаменателя на максимальную степень переменной р и воспользуемся свойствами пределов: предел частного равен частному пределов, предел суммы равен сумме пределов и .

Исходя из этого имеем, что .

Аналогично получим конечное значение функции, согласно

.

Получены значения и .

Составим таблицу и построим график функции. Данный расчет удобно выполнить в Приложении Microsoft Office в табличном редакторе Excel.

2 Определение переходной функции h(t)

Задача

Модель элемента задана в виде передаточной функции . Требуется построить график переходной функции данного элемента.

Решение

Переходная функция звена есть его реакция на единичную ступенчатую функцию.

.

Выполним обратное преобразование Лапласа в соответствии с рекомендациями, изложенными в примере 1.

.

Рассчитаем начальное и конечное значения функции по предельным теоремам Лапласа:

;

.

Теперь можно определить момент окончания расчета. Это может быть любой момент времени, когда становится понятен характер изменения сигнала.

Составим таблицу и построим график функции. Данный расчет удобно выполнить в Приложении Microsoft Office в табличном редакторе Excel.

3 Структурные преобразования

Задача

Преобразовать схему и найти передаточные функции системы в разомкнутом и замкнутом состоянии по управляющему и возмущающему воздействиям, передаточные функции ошибок по управляющему и возмущающему воздействиям, характеристическое уравнение САУ в замкнутом состоянии.

Решение

Для получения передаточной функции разомкнутой системы уберем главную обратную связь (ГОС). Далее проведем преобразования для упрощения схемы.

Первый шаг преобразования

,

и, кроме того, сделан перенос назад внешнего воздействия .

Второй шаг преобразования

Третий шаг упрощения

,

.

Здесь динамическое звено W₁₄(p) является передаточной функцией разомкнутой системы по управляющему воздействию W_р(p).

Передаточная функция по возмущающему воздействию определяется по формуле

.

Для определения передаточной функции замкнутой системы восстанавливаем ГОС.

Главная передаточная функция САУ имеет вид

.

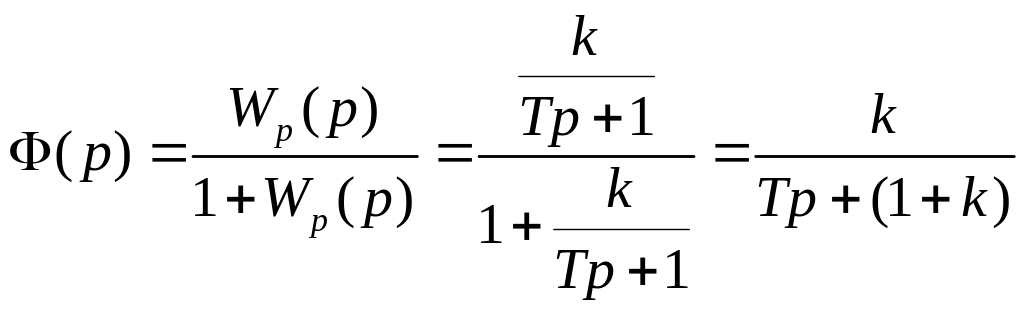Передаточная функция замкнутой системы для ошибки по задающему воздействию

.

Передаточная функция замкнутой системы по возмущающему воздействию определяется при условии равенства нулю задающего воздействия и равна

.

Передаточная функция для ошибки по возмущающему воздействию будет той же, что передаточная функция замкнутой системы по возмущающему воздействию , но с обратным знаком

.