5.4. Показатели колеблемости
Изучение колебаний уровней динамического ряда имеет важное значение для анализа и регулирования сезонных социальных процессов. Различают три основных типа колебаний.
Пилообразная или маятниковая колеблемость состоит в попеременных отклонениях уровней от тренда в одну и в другою сторону (рис. 5).
Рис. 5. Пилообразная колеблемость
Циклическая долгопериодическая колеблемость состоит в том, что отклонения уровней от тренда сначала постепенно увеличиваются, затем постепенно уменьшаются, и меняя свой знак на противоположный вновь начинают увеличиваться (рис. 6). Такая колеблемость свойственна, например, солнечной активности и связанными с ней процессами на Земле.
Рис. 6. Циклическая долгопериодическая колеблемость
Случайно распределенная во времени колеблемость возникает при наложении нескольких колебаний с различными циклами, но может проявляться в результате хаотичных колебаний основного действующего фактора (рис. 7).
Рис. 7. Случайно распределенная во времени колеблемость
Основными показателями силы колебания уровней являются: амплитуда отклонений уровней отдельных периодов или моментов от тренда, среднее абсолютное отклонение уровней от тренда, среднеквадратическое отклонение уровней от тренда. Относительное линейное отклонение от тренда и коэффициент колеблемости вычисляются путем деления соответствующих абсолютных показателей на средний уровень за весь изучаемый период.
Среднее линейное отклонение вычисляется из соотношения:
,
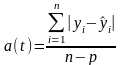где yi – фактический уровень;
-
выровненный уровень (тренд);
n – число уровней;
p – число параметров тренда (для линейной формы тренда p=2).
Среднеквадратическое отклонение вычисляется из соотношения:
.
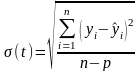5.5. Прогнозирование на основе тренда и колеблемости
Прогнозирование возможных в будущем значений признаков изучаемого объекта - одна и основных задач статистических методов исследования. Ведущую роль здесь играет расчет прогнозов на основе тренда и колеблемости динамического ряда. Методика статистического прогноза по тренду и колеблемости основана на их экстраполяции, т.е. на предположении, что параметры тренда и колебаний сохраняются до прогнозируемого периода. Это справедливо, если система развивается эволюционно в достаточно стабильных условиях. Обычно рекомендуют, чтобы срок прогноза не превышал одной трети длительности базы расчета тренда.
В качестве первого шага прогнозирования вычисляется точечный прогноз – значение тренда при подстановке в его уравнение номера соответствующего года. На втором шаге рассчитывается средняя ошибка прогноза положения тренда на соответствующий год:
,
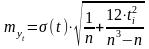где ti – номер года прогноза.
Пример 6. По данным таблицы 6 (числа зарегистрированных преступлений, связанных с незаконным оборотом наркотиков в Российской Федерации (в единицах) за год с 1996г. по 2010 г.) рассчитать параметры уравнения тренда, построить график, спрогнозировать число преступлений, связанных с незаконным оборотом наркотиков в 2011 году.
Решение. Промежуточные результаты сведем в таблицу.
Таблица 9
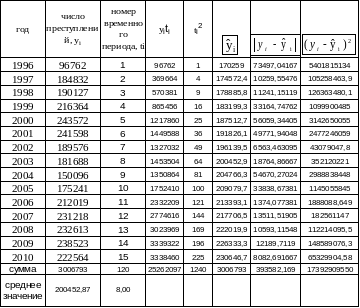
По формулам подсчитаем параметры уравнения тренда:
;
.
Таким образом, уравнение тренда имеет следующий вид:
Построим график динамического ряда с линией тренда (для упрощения построений воспользуемся табличным процессором MS Excel).
Рис. 8. Графическое изображение динамического ряда и линии тренда
Для расчета прогноза на 2011 год необходимо подставить в уравнение тренда номер временного периода для этого года – 16. Окончательно получаем точечный прогноз по числу раскрытых краж:
Средняя ошибка прогноза составит:
.
Для получения прогноза с уровнем надежности 0,9 следует среднюю ошибку умножить на величину t-критерия Стьюдента, равную 1,77 (при числе степеней свободы k=15-2=13). Следовательно, с вероятностью 0,9 можно утверждать, что ожидаемое значение данных преступлений составит 234960 64122,68 или от 170837,41 до 299082,78 случаев.