4. Числовые характеристики статистического распределения

Средние величины и их применение в юридической статистике.

С помощью средних величин можно сравнивать интересующие нас совокупности юридически значимых явлений по тем или иным количественным признакам и делать из этих сравнений необходимые выводы. Например, сопоставить судебную практику назначения уголовных наказаний в двух районах, схожих по уровню и структуре преступности. Средняя величина в статистике представляет собой обобщенную характеристику совокупности однородных явлений по какому-либо одному количественно варьирующему признаку.

Средние статистические величины имеют несколько видов, но все они относятся к классу степенных средних, т. е. средних, построенных из различных степеней вариантов: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая.

В юридической статистике самое широкое применение находит средняя арифметическая. Она используется при оценке нагрузки оперативных работников, следователей, прокуроров, судей, адвокатов, других сотрудников юридических учреждений; расчете абсолютного прироста (снижения) преступности, уголовных и гражданских дел и других единиц измерения; обосновании выборочного наблюдения и т. д.

Средней арифметической вариационного ряда называется сумма произведений всех вариант на соответствующие частоты, деленная на сумму частот:

,

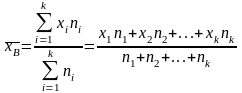где х_i – варианты дискретного ряда или середины интервалов непрерывного ряда распределения;

n_i – частоты вариант в вариационном ряду.

Средняя величина дает общую характеристику усредняемого признака, но не показывает, насколько она типична для данной совокупности.

Показатели вариации признака.

Показатели вариации (изменения, колебаний) позволяют измерить изменение величины количественного признака от одного объекта исследуемой совокупности к другому.

Размах вариации – это разность между максимальным и минимальным значениями признака

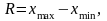
где R - размах вариации;

х_max – максимальное значение признака;

х_min – минимальное значение признака.

Следует отметить, что размах вариации весьма неустойчив и поэтому может служить лишь для грубой оценки.

Выборочная дисперсия Dв характеризует рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения. Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонений вариант от их среднего арифметического значения :

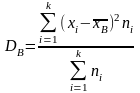
Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии:

Коэффициент вариации:

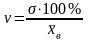
Коэффициент вариации является критерием типичности средней. Если коэффициент вариации меньше 10%, то изменчивость вариационного ряда принято считать незначительной, от 10% до 20% относится к средней, больше 20% и меньше 33% к значительной и если коэффициент вариации превышает 33%, то это говорит о неоднородности информации и необходимости исключения самых больших и самых маленьких значений.

Пример 4. В таблице 5 представлены данные о наказании за умышленное убийство за 1996 г.⁵ Вычислить числовые характеристики (среднее арифметическое, выборочную дисперсию и выборочное среднее квадратическое отклонение) данного интервального ряда распределения.

Таблица 5

Сроки лишения свободы, xi	До 1 года	1 - 2	2 - 3	3 - 5	5 - 8	8 - 10	10 - 15
Число осужденных, ni	10	3	16	78	516	1259	2921

Рассчитаем средний срок лишения свободы, то есть среднюю арифметическую. Для этого преобразуем интервальный ряд в дискретный. Найдем середины интервалов:

Дальнейшее вычисление проводится по формуле для подсчета средней арифметической.

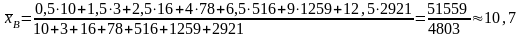(г.)

Вычислим значение выборочной дисперсии и выборочного среднего квадратического отклонения.

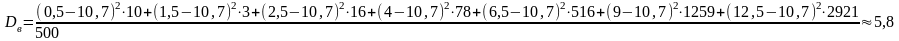
Найдем коэффициент вариации 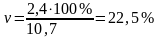. Он показывает, что изменчивость вариационного ряда значительна.