Основы юридической статистики

Вопросы лекции

1. Понятие юридической статистики 1

2. Первичная обработка материалов массовых статистических наблюдений 2

3. Графическое представление статистического распределения 4

4. Числовые характеристики статистического распределения 7

5. Ряды динамики 10

5.1. Понятие о рядах динамики и их виды 10

5.2. Показатели, характеризующие тенденцию динамики 12

5.3. Расчет параметров тренда 14

5.4. Показатели колеблемости 17

5.5. Прогнозирование на основе тренда и колеблемости 18

6. Статистические взаимосвязи 20

6.1. Функциональная и корреляционная зависимости 20

6.2. Условия применения корреляционно-регрессионного анализа 22

6.3. Задачи корреляционно-регрессионного анализа 23

6.4. Парная линейная корреляция 24

1. Понятие юридической статистики

Статистика – это общественная наука, изучающая количественную сторону массовых общественных явлений и процессов в неразрывной связи с их качественной стороной, в конкретных условиях места и времени.¹

Массовые общественные явления и процессы представляют собой, например, производство и потребление товаров, внутреннюю и внешнюю торговлю, рождаемость и смертность, доходы и расходы населения и т.д. Каждое из этих явлений и процессов состоит из большого количества однородных единиц, которые вместе взятые в конкретных условиях места и времени представляют собой статистическую совокупность. Изучение статистической совокупности с учетом индивидуальности каждой ее единицы и составляет основную задачу статистической науки. Как отрасль практической деятельности статистика предполагает сбор, обработку, анализ и публикацию данных, характеризующих наблюдаемый объект. Статистика позволяет определить меру взаимосвязи между явлениями и процессами.

В основе статистической методологии лежит совокупность количественных и качественных приемов анализа изучаемых явлений и процессов. Она широко использует математику, как наиболее точный инструмент исследования.

Общая теории статистики является методологической наукой, которая разрабатывает и определяет общие принципы и методы статистического исследования.

Отраслевые статистики – статистика промышленности, труда, транспорта, юридическая статистика и т.д. используют методы общей статистики. Юридическая статистика – отрасль статистической науки, имеющая дело с количественными показателями правовой и иной юридически значимой деятельности.²

2. Первичная обработка материалов массовых статистических наблюдений

Исходным пунктом исследования, проводимого с использованием статистических методов, является статистическое наблюдение, то есть научно организованный сбор информации о признаках исследуемых объектов. Статистическое наблюдение, проведенное на основе официального учета или путем специально организованного изучения, дает большое число сведений. Но эти данные разрозненны, для дальнейшего изучения их нужно систематизировать. Научная разработка и систематизация материалов статистического наблюдения является первым этапом проведения первичной обработки и называется статистической сводкой.

Составными элементами сводки являются: 1) разработка системы показателей, характеризующих преступность или другое социально-правовое явление в целом и ее отдельные группы (показатели могут быть количественными или качественными); 2) статистическая группировка полученных данных; 3) подсчет групповых и общих итогов; 4) оформление результатов в виде статистических таблиц или графиков.

В юридической статистике применяются три вида группировок: типологическая, вариационная (или структурная) и аналитическая.

Под типологической группировкой понимают расчленение изучаемой совокупности преступлений, преступников или других явлений, имеющих юридическое значение, на отдельные качественно однородные совокупности по важнейшим существенным качественным признакам. Например, это деление преступлений по категориям тяжести (небольшой тяжести, средней тяжести, тяжкие и особо тяжкие), личности виновных (мужчины и женщины, взрослые и несовершеннолетние, ранее судимые и несудимые) и т. д. Качественные признаки нередко переплетаются между собой, образуя сложную типологическую группировку деяний.

Вариационная, группировка статистических данных может производиться, чтобы изучить изменение структуры типически однородных групп преступлений, правонарушителей, гражданских исков и других показателей. При такой группировке однородная совокупность расчленяется по величине изменяющегося (варьирующегося) признака. Если в основе типологической группировки лежат качественные признаки, то в основу вариационной положены количественные (возраст правонарушителей, сроки наказания, суммы ущерба, суммы иска и т. д.).

Аналитическая группировка юридически значимых показателей позволяет обнаружить взаимосвязь и зависимость изучаемых явлений и процессов. В определенной мере эта задача решается и типологической, и структурной группировками. Но аналитическая группировка данных специально предназначена для решения этой задачи.

Пример 1. Пусть имеются данные о возрасте 100 рецидивистов, осужденных за грабеж и разбой:

18, 20, 32, 23, 20, 24, 22, 18, 29, 23, 19, 21, 18, 23, 18, 24, 27, 31, 19, 25, 27, 21, 28, 25, 16, 17, 27, 21, 19, 20, 19, 25, 18, 27, 22, 23, 19, 31, 32, 27, 19, 22, 30, 17, 22, 19, 18, 24, 20, 22, 17, 29, 21, 27, 17, 31, 25, 20, 24, 19, 26, 28, 21, 18, 26, 21, 20, 23, 26, 23, 19, 25, 21, 20, 18, 25, 33, 18, 33, 19, 33, 28, 31, 22, 30, 19, 26, 18, 29, 20, 29, 19, 23, 32, 17, 20, 33, 21, 33, 19.

Проведем вариационную группировку данных. После их упорядочивания в порядке возрастания получим следующий ряд:

16, 17, 17, 17, 17, 17, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 20, 20, 20, 20, 20, 20, 20, 20, 20, 21, 21, 21, 21, 21, 21, 21, 21, 22, 22, 22, 22, 22, 22, 23, 23, 23, 23, 23, 23, 23, 24, 24, 24, 24, 25, 25, 25, 25, 25, 25, 26, 26, 26, 26, 27, 27, 27, 27, 27, 27, 28, 28, 28, 29, 29, 29, 29, 30, 30, 31, 31, 31, 31, 32, 32, 32, 33, 33, 33, 33, 33.

Операция упорядочивания ряда числовых данных по возрастанию (убыванию) называется его ранжированием. После сводки материалы наблюдения принимают следующий вид, для большего удобства записываемый в виде таблицы.

таблица 1

Наблюдаемые значения возраста (х₁=16, х₂=17, ..., х₁₈=33) называются вариантами, а последовательность вариант, записанная в возрастающем порядке, - вариационным рядом или рядом распределения.

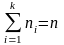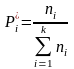Числа наблюдений в начале примера – это числа лиц n₁, n₂, ..., n₁₈ называются частотами. Относительной частотой называется отношение числа наблюдений данной варианты (n_i) к общему числу наблюдений ( ), т.е. . Отметим, что сумма относительных частот равна единице: .

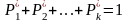Вычислим относительные частоты.

таблица 2

Теперь можно, например, подсчитать, сколько в России преступников, совершивших преступление в возрасте 18 лет. Доля 18-летних преступников 0,1. Умножив общее число лиц, нарушивших уголовный закон, на 0,1 получим искомое число.

Перечень вариант и соответствующих им частот называют статистическим распределением выборки. При соблюдении всех правил проведения выборочного исследования статистическое распределение выборки является экспериментальным отражением соответствующего закона распределения случайной величины и может служить основанием для анализа действующих факторов и закономерностей.

Вариационные ряды бывают дискретные и интервальные (непрерывные). Вариационный ряд называется дискретным, если в нем указаны конкретные значения варьируемого признака. Вариационный ряд называется интервальным (непрерывным), если предполагается, что варианты могут принимать любое значение в рамках указанных интервалов.

При построении интервального ряда необходимо выбрать оптимальное число групп. Малое число групп снижает разнообразие значений признака, а большое число групп может исказить форму распределения случайными колебаниями частот. Длина интервала должна быть постоянной для всех групп.

Количество интервалов также зависит от объема выборки. В качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал.

Рекомендуемое число интервалов для выборок разного объема:

таблица 3

Объем выборки	10-20	30-50	60-90	100-200	300-400
Число интервалов (k)	5	6-7	8	9	10