
- •Практическая работа 1. Факторный анализ доходов от грузовых перевозок методом цепных подстановок
- •Методические указания по проведению факторного анализа доходов от грузовых перевозок методом цепных подстановок
- •Практическая работа 2. Оценка целесообразности внедрения поточного производства в колесно-роликовом цехе вагоноремонтного депо
- •Методические указания по расчёту длительности производственного цикла и производительности при различных видах организации производства во времени
- •Практическая работа 3. Управление качеством. Выборочный метод.
- •Методические указания к решению задач по управлению качеством
- •Практическая работа 4. Оптимизация производственной программы с применением симплекс-метода
- •Методические указания к решению задач по оптимизации производственной программы
- •Библиографический список
- •Содержание
Методические указания к решению задач по оптимизации производственной программы
Введем условные обозначения:
i - номер машины;
j - номер производимого изделия;
bi - количество ресурсов (машино-часов) машины с номером i;
Найти max F=c1+c2+c3+...cj+...+cn
при условиях:
a11x1+a12x2+a13x3+...a1jxj+ ...+a1nxn<=b1
a21x1+a22x2+a23x3+...a2jxj+ ...+a2nxn<=b2
.......................................................................
an1x1+an2x2+an3x3+...anjxj+...+annxn<=bn
x1 > =0, x2 >=0, x3 >=0,…, xn >=0
Алгоритм симплекс-метода состоит из двух этапов. На первом этапе осуществляется построение допустимой производственной программы.
1. Построение канонической формы. Для каждого ограничения вводим
 --
дополнительную переменную.
--
дополнительную переменную.
2. Строится базис допустимого плана относительно этих переменных.
3. Рассчитываются симплекс- множители
 (23)
(23)
и показатели индексной строки
 (24)
(24)
На втором этапе выполняются итеративные процедуры оптимизации базиса задачи.
4. Выполняется проверка решения на оптимальность. Для задач на максимум целевой функции (прибыли) должно выполняться условие:
 (25)
(25)
Если условие оптимальности не выполняется, переход к п. 5; иначе получен оптимальный и допустимый план.
5. Выбор ключевого столбца. Из показателей индексной строки выбирается значение с наибольшим отклонением от условия оптимальности. Соответствующая переменная на следующей итерации входит в базис задачи. Выбор ключевой строки. Находится минимальное отношение показателей столбцов xiи aij при условии , что aij>=0.
6. Симплекс- преобразования:

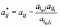 (26)
(26)
 (27)
(27)
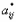 -
значение элемента в новом базисе;
-
значение элемента в новом базисе;
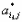 -
значение элемента ключевой строки в
новом базисе;
-
значение элемента ключевой строки в
новом базисе;
 -
значение элемента в текущем базисе;
-
значение элемента в текущем базисе;
 -
значение элемента ключевой строки в
текущем базисе;
-
значение элемента ключевой строки в
текущем базисе;
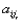 -
значение элемента ключевого столбца в
текущем базисе;
-
значение элемента ключевого столбца в
текущем базисе;
 -
значение ключевого элемента в текущем
базисе.
-
значение ключевого элемента в текущем
базисе.
Переход к п. 4.
Решение типового примера. Пусть на производстве имеется возможность четырех видов изделий, например, g1, g2, g3, g4. Для их производства привлекаются три вида ресурсов: b1, b2, b3. Для производства рассчитаны коэффициенты затраты ресурсов на выпуск каждого изделия, aij. Производственная система заинтересована в максимизации прибыли, поэтому в качестве критерия оптимальности используется прибыль на одно изделие cj. В качестве неизвестных примем выпуск изделий xj
Тогда, в соответствии с общей задачей линейного программирования можем составить математическое описание задачи производства четырех изделий при трех видах ресурсов:
.3x1+4x2+3 x3+1 x4 =max F
2x1+4x2+0 x3+8 x4<=12
7 x1+2 x2+2 x3+8 x4<=8
5 x1+8 x2+4 x3+3 x4 <=48
x1 >=0, x2 >=0, x3 >=0, x4 >=0
1. Построение канонической формы. Для каждого ограничения вводим Xj>=0 - дополнительную переменную. Поскольку у нас три ограничения, необходимо ввести три дополнительные переменные: X5, X6, X7. В результате имеем систему уравнений относительно ограничений и неравенств относительно переменных.
2 X1+4 X2+0 X3+8 X4+1 X5+0 X6+0 X7=12
7 X1+2 X2+2 X3+8 X4+0 X5+1 X6+0 X7=8
5 X1+8 X2+4 X3+3 X4+0 X5+0 X6+1 X7=48
X1 >=0, X2 >=0, X3 >=0, X4 >=0, X5 >=0, X6 >=0, X7 >=0.
2. Строится базис допустимого плана относительно этих переменных. Для этого приравняем 0 значения всех переменных относительно возможного выпуска изделий 1, 2, 3, 4 вида, т.е. X1= X2= X3= X4=0. Тогда имеем план выпуска изделий пятого вида в количестве 12 машино - часов/1час на единицу=12 единиц, соответственно изделий шестого вида составит 8 единиц, седьмого вида - 48 единиц.
На основе базиса допустимого плана построим специальную форму для решения задачи симплекс-методом. Здесь в столбце ci приведены показатели целевой функции переменных, входящих в базис задачи: с5=0, с6=0, с7 =0, в столбце pi - наименования самих показателей, X5, X6, X7 ,В столбце Xi приведены значения показателей: X5=12, X6=8, X7 =48. Первая строка таблицы содержит значения показателей cj. Вторая строка содержит наименования переменных канонической формы. Последняя - индексная строка содержит данные коэффициентов, рассчитываемых в п. 3.
ci |
pi, |
xi |
3 |
4 |
3 |
1 |
0 |
0 |
0 |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|||
0 |
x5 |
12 |
2 |
4 |
0 |
8 |
1 |
0 |
0 |
0 |
x6 |
8 |
7 |
2 |
2 |
6 |
0 |
1 |
0 |
0 |
x7 |
48 |
5 |
8 |
4 |
3 |
0 |
0 |
1 |
zj-cj |
F |
|
|
|
|
|
|
|
|
Остальные показатели на белом фоне представляют затраты машинного времени на выпуск единицы продукции.
3. Рассчитываются симплекс- множители (zj) и показатели индексной строки zj-cj,: где zj рассчитывается по формуле:
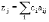 (28)
(28)
Рассмотрим таблицу, полученную на шаге 2, и заполним последнюю строку. Начнем с клетки относительно переменной x1: z1=c5*a51+ c6*a61+c7*a71. Имеем: z1=0*2+0*7+0*5=0; z1-c1=0-3=-3, и т.д.
ci |
pi, |
xi |
3 |
4 |
3 |
1 |
0 |
0 |
0 |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|||
0 |
x5 |
12 |
2 |
4 |
0 |
8 |
1 |
0 |
0 |
0 |
x6 |
8 |
7 |
2 |
2 |
6 |
0 |
1 |
0 |
0 |
x7 |
48 |
5 |
8 |
4 |
3 |
0 |
0 |
1 |
zj-cj |
F=0 |
-3 |
-4 |
-3 |
-1 |
0 |
0 |
0 |
|
Далее заполним клетку F= c5*x5+ c6*x6+c7*x7 = 0*12+0*8+0*48=0.
4.1. Выполняется проверка решения на оптимальность. Для задач на максимум целевой функции должно выполняться условие zj-cj>=0. В нашей таблице условие оптимальности не выполняется.
5.1. Выбор ключевого столбца. По данным индексной строки выбираем показатель z2-c2=-4 как имеющий наибольшее отклонение от условия оптимальности. Это ключевой столбец. Соответствующая переменная, X2, на следующей итерации войдет в базис задачи. Выберем ключевую строку из отношения: min{xi/a i2}={12/4;8/2;48/8}=12/4.Следовательно, строка с переменной x5 является ключевой. Клетка на пересечении ключевой строки (x5) и ключевого (X2) столбца называется ключевой. Ее значение равно 4.
6.1. Выполняются симплекс – преобразования по формулам 26 и 27.
Начнем преобразование таблицы с клеток ключевой строки x5 . Все ее элементы разделим на значение, равное 4, ключевой клетки. В связи с этим имеем: 12/4=3; 2/4=1/2; 4/4=1; 0/4=0; 8/4=2; 1/4=1/4 и.т.д. Занесем эти значения в клетки первой строки для переменной х2 следующей таблицы.
Рассчитаем значения клеток для строки с переменной х6: 8-12*2/4=2; 7- 2*2/4=6; 2-4*2/4=0 (все элементы этого столбца оказываются равными 0); 2-0*2/4=2 (все элементы ключевого столбца оказываются равными прежнему значению, кроме значения ключевой клетки, которая равна 1); 6-8*2/4=2; 0-1*2/4=-1/2; 1-0*2/4=1 (все элементы этого столбца оказываются равными прежнему значению); и.т.д.
Далее проводятся аналогичные расчеты для всех остальных клеток.
Получаем следующую таблицу.
ci |
pi, |
xi |
3 |
4 |
3 |
1 |
0 |
0 |
0 |
|||||
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
||||||||
4 |
x2 |
3 |
1/2 |
1 |
0 |
2 |
1/4 |
0 |
0 |
|||||
0 |
x6 |
2 |
6 |
0 |
2 |
2 |
-1/2 |
1 |
0 |
|||||
0 |
x7 |
24 |
1 |
0 |
4 |
-13 |
-2 |
0 |
1 |
|||||
zj-cj |
F=12 |
-1 |
0 |
-3 |
7 |
1 |
0 |
0 |
||||||
4.2. Выполняется проверка решения на оптимальность. В нашей таблице условие оптимальности для показателей индексной строки относительно переменных x3 и x1 не выполняется.
5.2. По данным индексной строки выбираем показатель z3-c3=-3, как имеющий наибольшее отклонение от условия оптимальности. Это ключевой столбец. Соответствующая переменная, X3, на следующей итерации войдет в базис задачи. Выберем ключевую строку: min{ xi/ ai3}={2/2;24/4}=2/2. Обратим внимание, что не рассматриваются коэффициенты меньше или равные нулю. Итак, строка с переменной x6 является ключевой. Клетка на пересечении ключевой строки и ключевого столбца будет на этот раз ключевой (2) . Теперь необходимо ввести переменную X3в базис задачи и вывести переменную x6.
6.2. Для ранее рассчитанной таблицы выполняются уже знакомые симплекс - преобразования относительно всех элементов. Получаем следующую таблицу.
ci |
pi, |
xi |
3 |
4 |
3 |
1 |
0 |
0 |
0 |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|||
4 |
x2 |
3 |
1/2 |
1 |
0 |
2 |
1/4 |
0 |
0 |
3 |
x3 |
1 |
3 |
0 |
1 |
1 |
-1/4 |
1/2 |
0 |
0 |
x7 |
20 |
-11 |
0 |
0 |
-17 |
-1 |
-2 |
1 |
zj-cj |
F=15 |
8 |
0 |
0 |
10 |
1/4 |
3/2 |
0 |
|
4.3. Выполняется проверка решения на оптимальность.
В нашей таблице условие оптимальности для показателей индексной строки относительно всех переменных выполняется, следовательно, получен оптимальный план.
Анализ оптимального плана решения задачи.
1. Рассмотрим содержание оптимального плана. Как следует из него, необходимо выпускать изделия второго (х2) и третьего (х3) вида в количестве 3 и 1 единиц. Это обеспечивает массу прибыли в 15 у.е. Остальные изделия в оптимальный план не попали. Значения соответствующих переменных х1=х4=0.
Вернемся к исходной модели:
2 X1+4 X2+0 X3+8 X4<=12
7 X1+2 X2+2 X3+8 X4<=8
5 X1+8 X2+4 X3+3 X4<=48
X1 >=0, X2 >=0, X3 >=0, X4 >=0
Подставим значения неизвестных в оптимальном плане в систему неравенств модели. Имеем: 12=12; 8=8; 28<48; X1 =0, X2 >0, X3 >0, X4 =0.
Как видно из расчетов, первые два неравенства выполняются как равенства, т.е. ресурсы используются полностью, а третье неравенство выполняется как строгое - имеются излишние ресурсы в количестве: 48-28=20. Этому соответствует значение дополнительной переменной х7=20. Если в базисе оптимального плана имеются дополнительные переменные со значениями более 0, то они всегда указывают на соответствующий излишек ресурсов (машино-часов).
2. Рассмотрим показатели индексной строки относительно переменных х1,х2,х3,х4. Если переменная находится в базисе оптимального плана, то значение соответствующего коэффициента в индексной строке равно нулю, что мы и видим для переменных х2 и х3. Экономический смысл показателей индексной строки для переменных, не вошедших в оптимальный план, выражается в потерях, которые может иметь производство, если захочет изготавливать соответствующие изделия. Иными словами, если производство первого изделия войдет в базисный (уже неоптимальный) план, то мы понесем убыток в 8 единиц прибыли: F=15-8=7 у.е.
3. Коэффициенты в индексной строке для дополнительных переменных характеризуют эффективность используемых ресурсов и называются двойственными оценками ресурсов. Чем выше оценка, тем эффективнее используется ресурс. Двойственная оценка характеризует прирост прибыли на единицу прироста соответствующего ресурса. Например, ресурсы второго вида наиболее эффективны для производства. Каждая единица прироста этого ресурса обеспечивает увеличение целевой функции на 3/2 единицы. Если ресурсы второго вида увеличатся на две единицы, то значение F составит: F=15+2*3/2=18 у.е. Двойственная оценка недоиспользуемых ресурсов всегда равна нулю, что и видно для нашего третьего ресурса. Прирост ресурсов третьего вида привел бы к росту их недоиспользуемых остатков.
