- 
= 6Z теңдеуі мына бетті анықтайды:
С) гиперболалық параболоид
- = 6z теңдеуі мына бетті анықтайды: А) екінші ретті бетті В)параболоид С)эллипстік параболоид Д) конус Е) цилиндр Ж) эллипсоид
сандық
қатарының мүшелері:
А) а3
=
-
F)
а1
=
-1
сандық
қатарының мүшелері:
D)
а1
=
7/2 Е)
а2
=
3
түзуі:
Е) 
(5;
2; -1) векторына G) 
түзуіне
параллель
= 1 түзуі А)
Оу
өсінен 3-ке тең кесінді қияды
=
А)
4
С)
оң сан
Д)
бүтін сан
A)
B)
C)бүтін
сан
D)оң
сан
E)-1
F)1
шегі:
А)1-ден
кіші С)0-ден үлкен Е)0,5-ке тең
A)128/2 B)0 C)64 D)62 E)192/3
A)2
B)-3
C)теріс
сан
D)1
E)0
А)
а = 2
анықталмаған
интеграл тең: A)
C)
E)
берілген гиперболаның эксцентриситетін
тап : A)
берілген гиперболаның эксцентриситетін тап :A)
Бүтін
сан
-
де
функциясының ең үлкен мәнін табыңдар:
А)
160/В)
320/2
дербес туындысы:A)
0 E) нақты сан
және 
түзулері:B)
бұрыш жасайдыE) перпендикуляр
қатарының бесінші мүшесі: A)рационал
сан B)
C)
D)4 E)теріс сан F)
G)оң сан
қатарының бесінші мүшесі:
А)
4
В)
оң
сан
қатарының бесінші мүшесі: Е) рационал сан F) 4
қатарының бесінші мүшесі:D)4
F)
G)Оң сан
қатарының тоғызыншы мүшесі:
А) 
В) рационал сан
қатарының тоғызыншы мүшесі: Е) F) оң сан
-
нің ќандай мәнінде қандай төмендегі
екі жазықтықтың біріне - бірі перпендикуляр
болады:
A)
36
В)
С)
-
нің қандай мәнінде төмендегі екі
жазқтықтың біріне - бірі перпендикуляр
болады:
,
.
А)
5
В)10/2
С)
Сандық қатарының мүшелері: 
сандық қатарының мүшелері:
А)
а1
=
-1
F)
а3
=
7/2
сандық қатарының мүшелері:
В)
а3
=
7/2
уневерсал ауыстырып қолдану арқылы
табылатын интеграл:B)
C)
E)
функциясы
үшін f
((0,0))
дербес туындысы; A)
2 B)
C) теріс сан D) 0 E) рационал сан F) оң сан
функциясының
алғашқы функциясы;
A) 14x
B) 2x
C)
D)
E)
F)
G)
функциясының алғашқы фунциясы:
, 
.
А+В матрицасын табу керек:А)
D)
,
векторлардың скаляр көбейтіндісін
табыңдар. A)
-9
C)-18/2
H)-27/3
:
В) бүтін сан
+ 
A)
4/10
B)
0,4
C)
2/10
D)
0,2
E)
0,8
F)
8/10
G)
0
=
A)
рационал сан С) оң сан Е) 3/2
=
В)бүтін
сан D)теріс
сан F)
-1
= 
, 
= 
векторларының скаляр көбейтіндісін
табу керек А)
-9/3
В)
-3
С)
-6/2
= 
векторының модулін тап А)
/2
В)
=
векторының
модулін тап:
В)
= 
векторының модулін тап:B)
C)
=
векторының
ұзындығын табыңдар:
А)3
F)
G)
= Е)
теріс сан
= 
,
= 
векторларының скаляр көбейтіндісін
табыңдар: Д)
34/2 Е) 17
=
,
= 
векторлардың
скаляр көбейтіндісін табу:
С) 0/8 D)
0
= :B)
= 1
берілген гиперболаның эксцентриситетін
тап:
С) 5/4 Е) 1,25
= 1 гиперболоиды: А)
әртүрлі жарты өстермен
В)
оz өсі бойымен созылған
С)
( 0; 0; 2) нүктесі арқылы өтеді
Д)
оу өсі бойымен созылған
Е)
екі қуысты
F)
ох өсі бойымен созылған
0X өсінен 2-ге тең кесінді қияды
A)
кіші жарты ось b=3
B)
эксцентриситет ε=1
C)
эксцентриситет ε=2
D)фокустар
арасындағы қашықтық 2c=8
E)
улкен жарты ось а=5
A)5/4
B)0,25
C)0,5
D)1
E)0
A)Бүтін сан
B)
18 C) бүтін сан
D)
z
теңдеуі мына бетті анықтайды
А) элиппстік параболоид B) төбесі
координата басы болатын параболоид
С) параболалық цилиндр D)конус E) эллипсоид
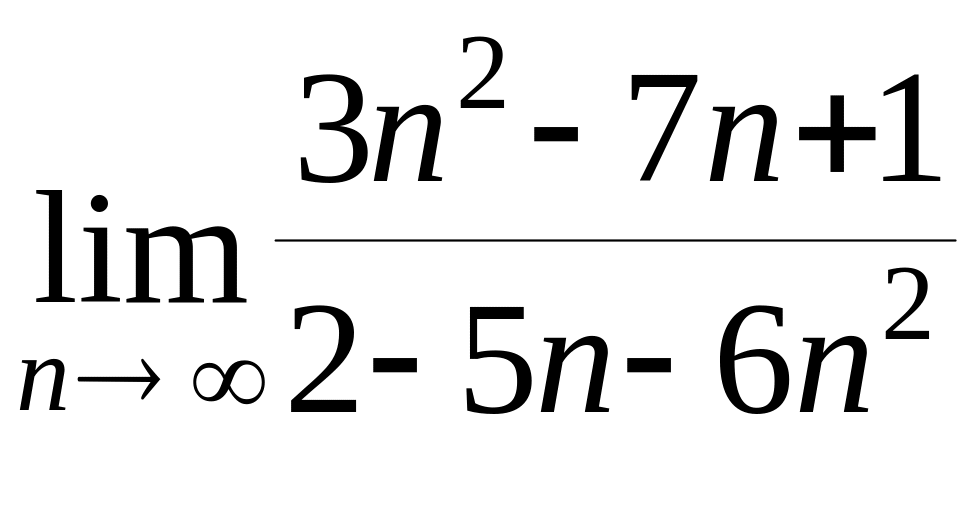А)
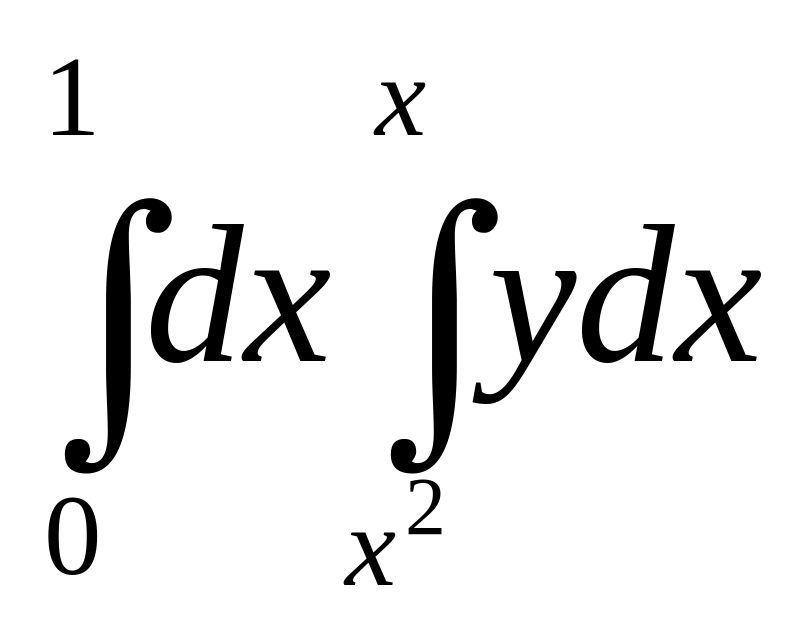А)
1/15 В) рационал сан С) оң сан
айқын емес функциясы үшін 
дербес туындысы: В)бүтін
сан
F)оң
сан
айқын емес функциясы үшін 
дербес туындысы:A)-2
B)1 C)-1 D)теріс сан E)бүтін сан F)8 G)оң сан
айқын
емес функциясы үшін
дербес туындысыА)
-1 В) теріс сан
айқын
емес функциясы үшін
дербес
туындысы: А)
бүтін сан
В)
2
анықталған
интеграл тең A)
1/4 B)0,25 D)2/8
анықталған
интеграл тең. A)
1/5 B)0,2 E)3/15
анықталған
интеграл тең: A)
B)
C)
анықталған интеграл тең: A) ¼ B)0,25 D)2/8
анықталмаған
интегралы тең: A)
B)
D)
берілген
гиперболаның эксцетриситетін тап; Е)
5/4
берілген эллипстің эксцентриситетін
тап:E)
0,8 F) 8/10
болғанда
функциясының туындысы
тең: A)8
D)
G)
бұрыш жасайды
В
оң сан D бүтін сан F теріс сан
векторлардың
скаляр көбейтіндісін табу керек:
A)8/2
B)12/3
және
түзулері;
C)
перпендикуляр D) 90
бұрыш
жасайды E) әртүрлі бұрыштық коэффициентке
ие
векторлардың
скаляр көбейтіндісін табу керек; B)
13
векторлардың
скаляр көбейтіндісін табыңдар. D)-3
G)
H)-9/3
векторларынан
ќўралєан параллелограмныѕ ауданы: 2,
4/2, 6/3
векторларының векторлық көбейтіндісі
деп төмендгі шарттарды қанағаттандыратын
векторын атайды:
векторларының
скаляр көбейтiндiсiн тап B)8
E)16/2
H)24/3
векторының
модулiн тап. A)
C)
H)
векторының
модулін тап:
А)
В)
векторының
модулін тапА)
В)
A)
векторының
ұзындығы тең А)
2В)
С)
векторының
ұзындығын табыңдар. A)
7
D)14/2
G)28/4
векторының
ұзындығын табыңдар. C)14
D)28/2
E)42/3
векторының
ұзындығын табыңдар. C)25
E)50/2
H)75/3
векторының
ұзындығын табыңдар.
A)
5
C)10/2
G)20/4
векторының
ұзындығын табыңдар.
A)
7
D)14/2
G)28/4
векторының
ұзындығын табыңдар.
B)13
D)26/2
H)39/3
векторының
ұзындығын табыңдар.
: 11,
33/3,
66/6
Векторының ұзындығын табыңдар.B)13 d)26/2 h)39/3
векторының
ұзындыєын табыңдар.: А)6
В)
С)
гиперболасы
үшін;
A) фокустар арасындағы қашықтық с=20 B)
фокустар арасндағы қашықтық
с=2
C)асимптоталар
теңдеуі y=
D) b=16 E) a=2 F) b=2
гиперболоиды:
А)
бірдей жарты өстермен /В)
өсі
бойымен созылған /Д)
бір қуысты
дәрежелік
қатарының жинақтылық радиусы тең: D)1
G)2/2
H)8/8
дәрежелік
қатарының жинақтылық радиусын табыңыз:
C)
D)
G)
дифференциалдық
теңдеуінің реті тең; A)
дифференциалдық
теңдеуін шешіңіз: D)
G)
H)
дифференциалдық
теңдеуінің реті тең: A)1
C)
E)
дифференциалдық
теңдеуінің реті тең: D)3
E)
G)
Дифференциалдық теңдеуінің реті тең: a)1 c) e)
дифференциалдық
теңдеуінің шешімін табыңыз B)
E)
G)
дифференциалдық
теңдеуінің шешімін табыңыз B)
D)
E)
дифференциалдық
теңдеуінің шешімін табыңыз: A)
F)
G)
дифференциалдық
теңдеуінің шешімін табыңыз: A)
D)
E)
дифференциалдық
теңдеуінің шешімін табыңыз: D)
E)
H)
дифференциалдық теңдеуінің шешімін табыңыз: A) F) G)
дифференциалдық теңдеуінің шешімін табыңыз: B) E) G)
дифференциалдық теңдеуінің шешімін табыңыз: B) D) E)
екi
нүктенiң арақашықтығын тап. A)5
C)10/2
H)15/3
екі
нүктенің арақашықтығын тап;
A)
екі
нүктенің арақашықтығын тап: C
D
E
есептеңіз:
½,
,
0,5
есептеңіз:
E)
8/3
G)
/3
H)
16/6
жазыктыгындагы
жаткан нукте: (1;2;1), (0;1;2), (1;-2;-1)
жазықтығы:
А)
Ох өсінен 2-ге тең кесінді қияды В) Оу
өсінен 3-ке тең кесінді қияды Д) Ох өсінен
2-ге тең кесінді қияды
жазықтығында
жатқан нүкте А)
жазықтығының модулін тап: A)(0;1;0) B) (0;3;1) C) (1;-1;2) D)(1;2;-1) E)(1;2;1) F)(0;1;2)
және 
векторларының векторлық көбейтіндісі
деп төмендегі шарттарды қанағаттандыратын
векторларын атайды:B)
векторына да, 
векторына да перпендикулярF) ұзындығы
және
векторларынан құрылған паралелограммның
ауданына теңG) осы векторлармен реттелген
оң үштік құрайды
және
векторлары m - нің қай мәнінде перпендикуляр
болады:
B)2
D)
E)
және
нүктелері арқылы өтетін түзудің теңдеуі:
А)
В)
Е)
және
нүктелері берілген.
векторының ұзындығы: А)
5 В) бүтін сан
және нүктелері берілген. кесіндісінің ортасының абсциссасы А) оң сан С)3,5
және 
түзулері :D)
параллельE) 
бұрыш жасайды
F)
бағыттаушы векторына ие
және
түзулерінің арасындағы бұрыш табу
формуласын көрсетіңіз:A)
B)
C)
және
түзулерінің паралльлелдік шартын
көрсетіңіз:
,
,
және
нүктелері
берілген.
кесіндісінің ортасының ординатасы А)
0 В) бүтін сан
және
түзулері:
А)
перпендикулярВ) 900
бұрыш жасайды
интегралын
есептеңіз: А)
G)
H)
интегралын
есептеңіз: C)
E)
G)
интегралын есептеңіз: А) G) H)
интегралын
табыңыз: C)
E)
H)
интегралын
табыңыз: D)
G)
H)
интегралын
табыңыз: A)
C)
E)
интегралын табыңыз: C) E) H)
интегралын
табыңыз: D)
G)
H)
интегралын
табыңыз: E)
F)
G)
интегралын табыңыз: A) C) E)
интегралын
табыңыз: A)
C)
F)
комплекстік
саны мынандай тригонометриялық түрде
жазылады: A)
B)
E)
Коши
есебін шешіңіз:
A)
E)
H)
қатарларының
қайсысы жинақты қатар болады: A) 2 G)4/2
H)8/4
қатарының бесінші мүшесі А)
4
В)
рационал сан
қатарының
бесінші мүшесі А)
оң санВ)
С)
4
қатарының
тоғызыншы мүшесі:
А)
B)
C)
D)
E) теріс сан
қисығына х=-1 нүктеде жүргізілген
жанаманың бұрыштық коэффициенті: 1 
:
бүтін
сан
матрицасы
берілген.
алгебралыќ
толыќтауышты есептеѕіз: 6, 18/3, 12/2
матрицасының рангы:C)
1-ден
артықD)
3G)
2-ден артық
нїктесінен
тїзуіне дейінгі ќашыќтыќ неге теѕ: 3,5,
7/2, 35/10
-
нің қандай мәнінде қандай төмендегі
екі жазықтықтың біріне - бірі перпендикуляр
болады:
:
A)
36
D)
G)
нүктесінде
-нің
мәні, егер
А)
-1
нүктесінен
түзуіне дейінгі қашықтықты табыңыз. A)
1 В)
С)
нүктесінен
түзуіне дейінгі қашықтықты табыңыз. A)
4 В)
С)
параболасымен
шектелген фигураның ауданын есептеңіз:
A)
D)
G)
сандық
қатарының мүшелері;
B)
C)
сандық қатардың мүшелері: В)
С)
Сандық қатардың мүшелері: В)
F)
сандық
қатарының мүшелері:
A)
B)
C)
D)
Е)
векторлардың аралас көбейтіндсін табу: A) 0 B) 57/3 C) 17 D) 19/2 E) 51/3 F)34/2
сандық
қатарының мүшелері
А)
B)
C)
D)
E)
F)
Сандық қатарының мүшелері:
C) 
D)
E)
сандық
қатарының мүшелері: А)
В)
С)
D)
Е)
сандық
қатарының мүшелері; B)
C)
E)
сандық қатрының мүшелері: A)
B)
сфеасы үшін: A)R=81
B)центрі
(0;0;0) нүктеде
сызыќтыќ
теѕдеуініѕ
-ін
есепте: -50, -100/2 ,
-150/3
сызықтық
біртекті дифференциалдық теңдеуінің
жалпы шешімін табыңыз:
A)
C)
G)
сызықтық
біртекті дифференциалдық теңдеуінің
жалпы шешімін табыңыз. A)
C)
F)
тендеуінің
жалпы шешімін табыңыз A)
C)
F)
теңдеуі мына бетті анықтайды: А)
эллипсиод
В)
гиперболалық параболоид
С)
эллипстік параболоид D) тармағы 0z өсімен
оң бағытталған параболоид
Е)
төбесі координата басы болатын параболоид
y=
функциясының
туындысы: А)
теңдеуіне
сәйкес біртекті сызықты теңдеуінің
жалпы шешімін көсетіңіз: A)
C)
E)
y=5x+7
және y=2/3x+1 түзулерінің арасындағы
бұрыштың аралығы: D)
[
теңдеуінің
жалпы шешімін табыңыз: A)
D)
G)
H)
теңдкуінің
жалпы шешімін табыңыз: D)
G)
H)
тїзуініѕ
бўрыштыќ коэффициентін табыѕыз: 2/3,
,
тїзуініѕ
бўрыштыќ коэффициентін аныќтаѕыз: 5/4,
1,25,
10/8
тїзуініѕ
бўрыштыќ коэффициентін табыѕыз: 7/2,
3,5, 14/4
түзуі
А)
Оу өсіне параллель
түзуі
А)
Ох өсімен 450
бұрыш жасайды В) Оу өсінен 3-ке тең кесінді
қиядыА)
нүктесі арқылы өтеді
түзуі: A)Oy
өсінен
6-ға тең кесінді қияды
B)
X+y-8=0
жалпы теңдеуге тең
C)
Х+2y-3=0 жалпы
теңдеуге ие
түзуі:D)
түзуіне параллельE)
нүктесі арқылы өтеді
түзуінде
жатқан нүкте: D
(1;5) E (0;7)
5(y```
-3y``*
=0
дифференциалдық теңдеуінің реті тең:
D) 4*
E) 4*
F)
түзууіА)
бұрыштық коэффициентке тең В) Ох өсімен
1350
бұрыш жасайды
универсал ауыстырып қолдану арқылы
табылатын интеграл: А)
функцияның
кему аралығын табыңыз:
B)
C)
E)
функциясы
берілген
А(2;1) нүктесіндегі
нің
мәні; A)-8 B)-
F)-2
функциясы
берілген.
A(1;1) нүктесіндегі
нің
мәні: A)4 B) 2
C)
D)
E)
F) 8