Федеральное Агентство по образованию

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра физики

ОТЧЕТ

Лабораторная работа по курсу "Общая физика"

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ

Преподаватель Студент группы

___________ /____________. / __________ / /

___________201_ г. __________ 2011 г.

2011

1. ЦЕЛЬ РАБОТЫ

Целью работы является изучение работы колебательного контура, свободных затухающих электромагнитных колебаний и их характеристик.

2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА

Схема установки представлена на рис.3.1. Колебания в контуре возбуждаются с помощью генератора импульсного напряжения.

Рис.2.1 Принципиальная электрическая схема установки

Схема смонтирована на съемной панели лабораторного макета. В качестве резистора в RP1 в колебательном контуре используется переменное сопротивление, максимальное значение которого находится в зависимости от номера съемной панели (470 Ом, 680 Ом и др.) и устанавливается поворотом ручки потенциометра по часовой стрелке в крайнее положение. При повороте ручки против часовой стрелки в крайнее положение значение сопротивления RP1=0. В этом случае активное сопротивление колебательного контура складывается из сопротивления соединительных проводов контура и активного сопротивления катушки индуктивности, . В дальнейшем это сопротивление необходимо рассчитать по результатам измерений.

Возбуждение контура производится периодически от генератора импульсного напряжения I, регистрируются колебания на осциллографе III. Каждый импульс, подаваемый с генератора на колебательный контур, возбуждает один цуг затухающих колебаний.

Измерения амплитуды и периода колебаний осуществляется непосредственно с помощью осциллографа.

3. Основные расчетные формулы

Логарифмический декремент затухания определяется по формуле:

, (3.1),

Сопротивление и индуктивность найдем из системы уравнений

δ₁= R_x/(2*L) (3.2)

δ₂ = (R_x+RP₁)/(2*L) ,

где δ₁- коэффициент затухания для R_x, δ₁- коэффициент затухания для R_x+RP_1, L – индуктивность конура, R_x, R_x+RP₁ - сопротивление

Определим длительность периода по формуле:

Рассчитаем собственную частоту:

ω₀ = √(1/ L*C (3.3)

И частоту собственных затухающих колебаний контура:

(3.3)

Определим длительность периода по формуле:

(3.4)

При слабом затухании ()добротность равна:

. (3.5)

Сопротивление контура, при котором наступает апериодический процесс, называется критическим и определяется из условия ,

. (3.6)

4. Результаты работы и их анализ.

Измеренные значения и результаты их обработки приведены в таблице 4.1.

Таблица 4.1

Результаты измерений

Значение активного сопротивления контура R	Номер измеряемой амплитуды n	Значение амплитуды Un, В	Значение логариф-мического декремента затухания	Среднее значение		Период затухающих колебаний , с
R=RX	1	0,713			0	0,000939
	2	0,597	0,178	0,19	0,1776	0,000955
	3	0,493	0,191	0,19	0,369	0,00097
	4	0,401	0,207		0,5755	0,00097
	5	0,328	0,201		0,7765	0,00097
R=RX+RP1	1	0,367			0	0,00097
	2	0,205	0,582		0,5824	0,000986
	3	0,116	0,569	0,58	1,1518	0,000986
	4	0,0638	0,598		1,7496	0,00097
	5	0,0365	0,558		2,308	0,00097

Проверим справедливость экспоненциального характера убывания амплитуды со временем:

Построим график зависимости ,

δ – угол наклона касательной (физический смысл в данном уравнении коэффициент затухания).

Построим линеаризованный график для R₁ и для R₂

Рисунок 4.1. Зависимость от nT, для R₁ и для R₂

Находим угловой коэффициент прямой по формуле:

δ₁ =Δ()/ Δ(nT)= 200,5 (с^-1)

δ₂ = 592,7 (с^-1)

Теперь ,зная δ₁ и δ₂, определим величину индуктивности

Т.к. составим систему уравнений, для L и R_x

δ₁= R_x/(2*L)

δ₂ = (R_x+RP₁)/(2*L)

Решая эту систему уравнений находим L = 0.5 Гн и R_x= 204 Ом

Рассчитаем собственную частоту и частоту собственных затухающих колебаний контура, зная что С =0.047 мкФ

ω₀ = √(1/ L*C) = 6459 (рад/с)

для δ₁

ω₁ = 6456 (рад/с)

для δ₂

ω₂ =6432 (рад/с)

Определим длительность периода по формуле:

Для R₁

T_ан1= 0,000972(с)

Для R₂

T_ан2= 0,000976 (с)

Найдем среднее значение периодов:

= 0.000961 (с)

=0.000976 (с)

Сравним измеренные , и вычисленные , значения периодов, вычислив отличия в процентах:

= =1.1%

== 0%

Оценим значение критического значения R_кр по формуле

R_кр=6588 (Ом)

И определим добротность колебательного контура

Q₁ = 16,2

Q₁ = 5.4

Видно, что добротность уменьшается

5. ВЫВОДЫ

В данной работе был изучен колебательный контур свободных электромагнитных затухающих колебаний, рассчитаны параметры данного контура: индуктивность L = 0.50 Гн, активное сопротивление катушки индуктивности R_x= 204 Ом, собственная частота и частота собственных затухающих колебаний контура ω₁ = 6456 (рад/с), ω₂ =6432 (рад/с), определена добротность колебательного контура Q₁ = 16,2 Q₁ = 5.4. В справедливости закона экспоненциального характера убывания амплитуды можно убедиться анализируя график, линейность графика от (n*T) и свидетельствует о выполнимости закона

6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какова цель работы? Дайте определение понятиям «затухающие колебания», «свободные колебания»

Ответ: Целью данной работы является изучение работы колебательного контура, свободных затухающих электромагнитных колебаний и их характеристик.

Затухающими колебаниями называются колебания, энергия которых уменьшается с течением времени. Свободные колебания - колебания, совершающиеся в системе при отсутствии внешнего воздействия за счет первоначально внесенной энергии, отклоняющие эту систему от состояния устойчивого равновесия

2. Какие колебания называются периодическими и являются ли затухающие колебания периодическими?

Ответ: Затухающие колебания не являются периодическими, так как максимальное значение колеблющейся величины Uj, достигаемое в некоторый момент времени t_s, в последующем (при t> t_s ) никогда не повторяется. Однако при затухающих колебаниях колеблющаяся величина обращается в нуль, достигает максимальных и минимальных значений через равные промежутки времени.

3. С помощью какой системы можно получить свободные электромагнитные колебания?

Ответ: Для возбуждения и поддержания электромагнитных колебаний используют колебательный контур, который представляет собой замкнутую цепь, состоящую из последовательно соединенных конденсатора емкостью С, катушки индуктивности L и омического сопротивления R. Причем омическое сопротивление включает в себя сопротивление соединенных проводов, сопротивление провода катушки индуктивности и сопротивление включенного в контур резистора.

4. Изменение каких физических величин осуществляется в контуре по колебательному закону?

Ответ: Изменение напряжения осуществляется в контуре по колебательному закону.

5. Как возникают в контуре электромагнитные колебания?

Ответ: Рассмотрим как возникают колебания в контуре. В начальный, момент с помощью генератора одиночных импульсов конденсатор заряжается до некоторой разности потенциалов U на его обкладках. При этом обкладкам конденсатора сообщен заряд ± q. Энергия электрического поля конденсатора Wq⁼ CU /2. Если теперь генератор отключить, а конденсатор замкнуть на катушку с индуктивностью L, то начнется его разрядка и в катушке возникнет ток. Это возрастающий от нуля ток приводит к возникновению магнитного поля. Следовательно, энергия электрического поля между обкладками конденсатора постепенно переходит в энергию магнитного поля катушки. В момент разрядки конденсатора ток в катушке достигает максимального значения и энергия магнитного поля Wi = LI 12. Когда полностью разрядился конденсатор, то, казалось бы, ток в катушке должен прекратиться. Но уменьшению тока в катушке препятствует явление самоиндукции, поддерживающее ток в прежнем направлении. Этот убывающий ток продолжает переносить заряды от одной обкладки конденсатора к цругой в том же направлении и перезаряжает конденсатор. Перезарядка заканчивается, когда ток становится равным нулю. В этот момент энергия магнитного поля катушки переходит в энергию электрического поля конденсатора. В следующий момент начинает разряжаться конденсатор, при этом ток течет в обратном направлении Разрядный ток возрастает, пока конденсатор не разрядится j полностью, а затем убывает, но вследствие явления самоиндукции снова перезаряжается конденсатор и контур возвращается в исходное состояние. Этим завершается один период колебаний в контуре Взаимное превращение энергии электрического и магнитного полей сопровождается потерями энергии на нагревание проводников. И если энергия не пополняется извне, то колебания в контуре затухают- амплитуда тока каждого последующего колебания меньше амплитуды предыдущего колебания. Чем больше омическое сопротивление контура, тем быстрее затухают колебания в нем.

6. Чем обусловлено затухание колебаний в контуре?

Ответ: Потерей энергии колебательного контура на омическое сопротивление проводников.

7. Какими параметрами контура определяется частота собственных незатухающих колебаний и частота собственных затухающих колебаний? Как соотносятся между собой эти частоты?

Ответ: Частота собственных колебаний определяется L и C.

8. Какая характеристика является количественной характеристикой убывания амплитуды затухающих колебаний? Какими параметрами контура она определяется?

Ответ: Добротность является количественной характеристикой убывания амплитуды затухающих колебаний. Она определяется частотой, индуктивностью и ёмкостью

9. Что характеризует коэффициент затухания и как он определяется в данной работе?

Ответ: Амплитуда затухающих колебаний уменьшается с течением времени тем быстрее, чем больше коэффициент затухания , в данной работе он определяется как δ₁= R_x/(2*L)

10. Как влияет коэффициент затухания на (условный) период затухающих колебаний в контуре?

Ответ: С увеличением коэффициента затухания период затухающих колебаний уменьшается.

11. По какому закону изменяется со временем амплитуда затухающих колебаний? Каким образом подтверждается справедливость этого закона?

Ответ: Амплитуда затухающих колебаний изменяется по экспоненциальному закону. Справедливость данного закона можно проверить в линейности графика Линейность графика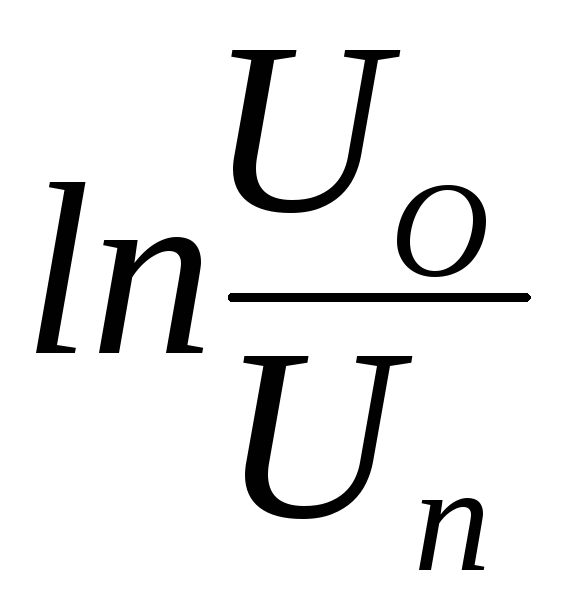 от (n*T)

12. Что называется временем релаксации?

Ответ: Промежуток времени , в течение которого амплитуда затухающих колебаний уменьшается в раз, называется временем релаксации.

13. На какие характеристики колебаний и как влияет величина активного сопротивления колебательного контура?

Ответ Чем больше активное сопротивление, тем быстрее затухнут первоначальные колебания, уменьшатся амплитуды тока и напряжения

14. К изменению каких характеристик колебаний и колебательного контура приведет изменение индуктивности контура?

Ответ: Изменение индуктивности контура приведет приведёт к изменению реактивного сопротивления и собственной частоты колебательного контура.

15. Какое условие необходимо выполнить при подборе элементов (R, L, C) электрического колебательного контура, чтобы изменение напряжения на конденсаторе осуществлялось по колебательному закону?

Ответ: Необходимо выполнить условие

16. Добротность колебательной системы, как она определяется?

Ответ: Добротность пропорциональна числу колебаний, совершаемых за промежуток времени, в течение которого амплитуда колебаний уменьшается в раз.

17. Как нужно изменить параметры контура, чтобы при однократной зарядке конденсатора, его разрядка осуществлялась по апериодическому закону?

Ответ: Необходимо подобрать такое значение индуктивности и ёмкости чтобы:

18. Как изменяются логарифмический декремент затухания и добротность контура, если известно, что при изменении параметров контура (R, L, C) число колебаний, за которое амплитуда уменьшается в е раз, увеличилось на десять колебаний?

Ответ: Логарифмический декремент затухания уменьшиться на 0,1, а добротность контура увеличится на 10.

19. Выполняется ли в реальном колебательном контуре закон сохранения электромагнитной энергии?

Ответ: Да, если учитывать все потери к колебательном контуре.

20. Почему при выводе основного уравнения свободных затухающих колебаний в контуре, где протекают переменные токи, используют закон Ома и правила Кирхгофа, полученные для постоянного тока?

Ответ: Потому что что размеры контура l не слишком велики (т.е. l<c/, где с – скорость света, с которой распространяются электромагнитные колебания; l – длина контура;  - частота колебаний), то можно считать, что мгновенное значение тока будет практически одинаково во всех точках контура. Удовлетворяющие такому условию токи называются квазистационарными.

21. Вывести основное уравнение свободных затухающих колебаний в электрическом колебательном контуре.

Ответ: Дифференциальное уравнение, описывающее свободные затухающие колебания линейной системы – электрического колебательного контура:

где U_L – падение напряжения на индуктивности, U_С – падение напряжения на емкости, U_R – падение напряжения на резисторе, или

Учитывая, что , и разделив этоуравнение на L, получим следующее уравнение

Так как величина заряда на обкладках конденсатора пропорциональна разности потенциалов на них (q=CU), то уравнение, описывающее изменение напряжения на конденсаторе, будет аналогично предыдущему уравнению, т.е.

Введя обозначения , , получим

где - коэффициент затухания, - частота собственных незатухающих колебаний контура. Данное уравнение является линейным дифференциальным уравнением второго порядка с постоянными коэффициентами и описывает свободные затухающие колебания.

При условии решение уравнения имеет вид

где - начальная фаза, - частота свободных затухающих колебаний, - амплитуда затухающих колебаний.