Физические основы оптоэлектроники (Контрольная №2 вариант№4. по метод. Давыдов В.Н.спец.210405)

Федеральное агентство по образованию

Томский межвузовский центр дистанционного образования

Томский государственный университет

систем управления и радиоэлектроники (ТУСУР)

Контрольная работа №2

(Вариант № 4)

по дисциплине «Физические основы оптоэлектроники»

(Учебное пособие «Физические основы оптоэлектроники»,

Автор : В.Н. Давыдов

Томск - 2004 г.

Выполнил:

студент ТМЦДО

22.10.2011 г.

2011 г

Задание №1

Рассчитать величину активного сопротивления, находящегося при температуре Т=300 К, если амплитуда теплового шума, регистрируемого на нём вольтметром с полосой пропускания , составляет .

Решение.

Эта задача на использование теоремы Найквиста: уровень шумового напряжения, образующего на активном сопротивлении в заданной полосе частот, равен:

_{Из данного вырвжения выразим величину активного сопротивления:}

Ом.

Таким образом, ответ на поставленный вопрос таков: величина активного сопротивления равна R Ом.

Ответ: R Ом.

Задание №2

Определить суммарное время жизни неравновесных носителей заряда (фотон+фотон) в германиевом образце n-типа проводимости с концентрацией донорной примеси находящемся при температуре Т=300 К, если известно, что внутренняя квантовая эффективность генерации оптического излучения в этом образце составляет 0,68.

Решение.

Исходными выражением для определения параметров внутренней квантовой эффективности является выражение, в котором неизвестными величинами являются время жизни излучательной рекомбинации и время жизни без излучательной рекомбинации :

Время жизни излучательной рекомбинации зависит от уровня легирования полупроводника по закону:

Из табличных данных известно, что время излучательной рекомбинации в собственном германии составляет

Поэтому по выражению будим иметь:

Суммарное время жизни выразим и подставим числовые значения из формулы:

Ответ:

Задача №3

Определить величину модуля упругости нематика, если известно, что величины диэлектрической проницаемости этого вещества вдоль оси молекулы и перпендикулярно ей при температуре равны соответственно, а напряжение перехода Фредерикса в нём составляет 1,4 В.

Решение.

Для решения данной задачи воспользуемся выражением, из него выразим модуль упругости К:

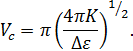
где -анизотропия диэлектрической проницаемость жидкого кристалла.

.

Будем решать задачу в системе СГСЕ, а полученный результат переведём в систему СИ.

Подстановка в данное выражение численных значенийпараметров жидкого кристалла даёт величину модуля упругости:

Ответ: