1.3 Расчет спектральной плотности дискретизированного сигнала.

Спектральную плотность дискретной последовательности найдём по следующей формуле, применив ППФ:

Для облегчения расчетов произведем нормировку делением на число отсчетов, в этом случае формула приобретает упрощенный вид:

Рис.1.5- График спектральной плотности аналогового и цифрового сигнала

Анализируя рисунок 1.5 можно сделать очень важный вывод: при дискретизации сигнала во временной области спектральная плотность становится периодической функцией частоты с периодом, равным _д. В то время как континуальный сигнал имеет апериодический спектр.

1.4 Расчет коэффициентов с помощью дискретного преобразования Фурье.

Найдем прямое дискретное преобразование Фурье (ПДПФ), установив однозначную связь между временными отсчетами сигнала и отсчетами его спектральной плотности. Коэффициенты рассчитаем по формуле:

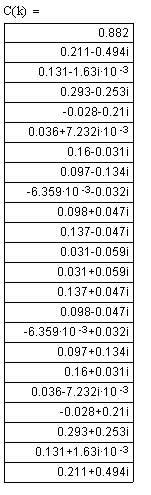, где ,

Рис 1.6 – Отчеты спектральной плотности, полученные по ДПФ

1.5 Восстановление исходного сигнала по дпф

По найденным коэффициентам ДПФ восстановим исходный сигнал.

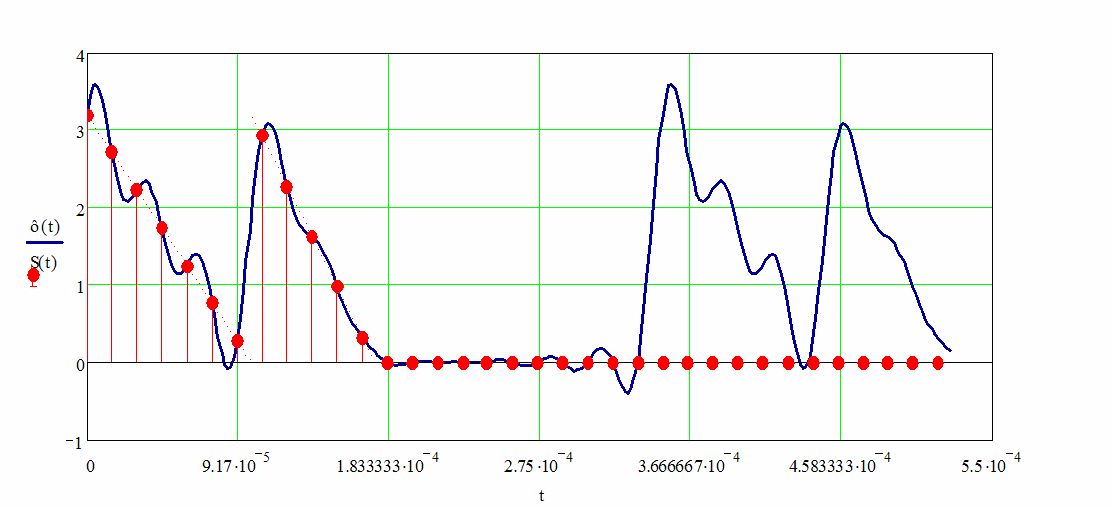
Рис. 1.7 - Аналоговый сигнал, восстановленный по коэффициентам ДПФ

Восстановленный сигнал является периодической функцией времени. Он точно проходит по отсчетам выборки на первом периоде. Очевидно, что при большем значении N восстановление будет точнее.

1.6 Z-преобразование дискретной последовательности

Прямое Z-преобразование последовательности определяется формулой

.

Функцию называютZ-образом последовательности .

Для того чтобы на основании Z – образа последовательности отчетов было возможно получить спектральную плотность, необходимо сделать замену вида

На рисунке 1.8 изображен модуль спектральной плотности дискретизированного сигнала, полученной на основе Z – преобразования (с учетом нормирования относительно числа степеней свободы N=23).Для сравнения на этом же рисунке изображен модуль спектральной плотности аналогового сигнала.

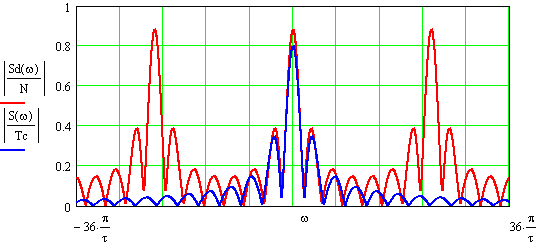
Рис. 1.8 – Модули спектральных плотностей исходного аналогового и дискретизированного сигналов.

1.7 Восстановление аналогового сигнала с использованием ряда Котельникова.

Восстановленный сигнал представляет собой сумму функций Котельникова с весами, равными отчетам сигнала.

Рис. 1.9 Аналоговый сигнал, восстановленный по ряду Котельникова

Как видно из рисунка 1.9, восстановленный сигнал остался апериодическим, а его форма напоминает исходную.

2 Синтез цф Чебышева по заданной ачх цифрового фильтра

2.1 Определение параметров ачх аналогового фильтра прототипа

Проектируемый цифровой ФНЧ должен удовлетворять следующим условиям:

1.Частота срезапо уровню 3 дБ должна быть

2.Затухание в полосе задержания не менее

3.Неравномерность АЧХ в полосе пропускания не более

Переведем цифровые критерии в аналоговый эквивалент по формуле

Полагая ,пересчитаем в аналоговые частоты

Сравним между собой соотношения цифровых и аналоговых частот

Чтобы обеспечить затухание  = 24дБ, надо выбрать фильтр порядка n = 3.

АЧХ аналогового ФНЧ Чебышева описывается следующим выражением:

где -параметр, характеризующий неравномерность АЧХ в полосе пропускания;

-полином Чебышева первого рода порядка n.

Напишем полином порядка n=3

Т₃(х)=4х³-3х

Таким образом, АЧХ анализируемого фильтра выглядит следующим образом

Рис.2.10 - АЧХ фильтра Чебышева третьего порядка