1. Новые контрольные / математика-5

Томский межвузовский центр дистанционного образования

Томский государственный университет систем управления и радиоэлектроники (ТУСУР)

Кафедра промышленной электроники (ПрЭ)

Контрольная работа №5

по дисциплине «Высшая математика»

Учебное пособие А.А.Ельцов «Интегральное исчисление. Дифференциальные уравнения»

Выполнил:

студент ТМЦДО

специальности 210405

Группы

2010

Вариант №7

Задание 1.

Найти неопределенные интегралы:

;

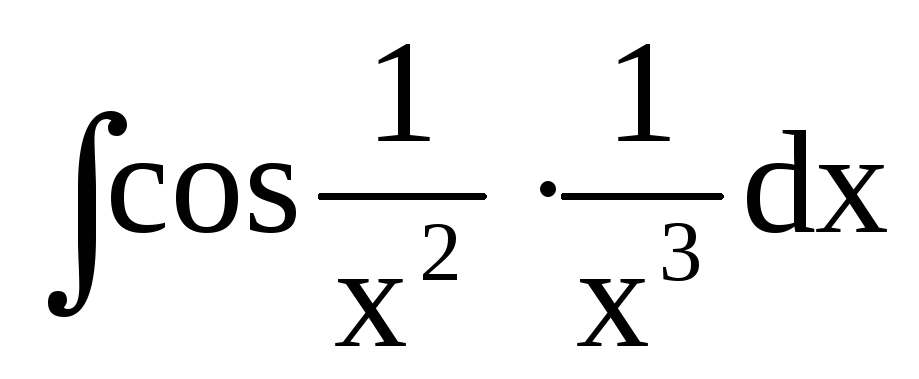Решение:

1. Пусть , тогда , значит .

2. Пусть , тогда , значит .

3. Пусть , тогда , значит .

4. Пусть , тогда , значит .

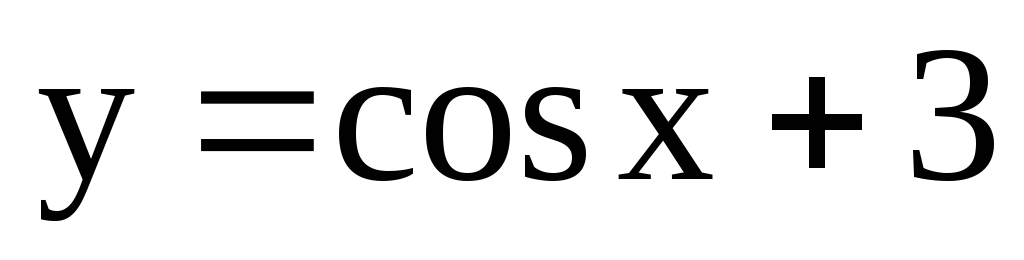5. Пусть , , тогда , . Используя формулу интегрирования по частям, получим: .

6. Пусть , тогда , значит

.

7. Пусть , тогда , значит

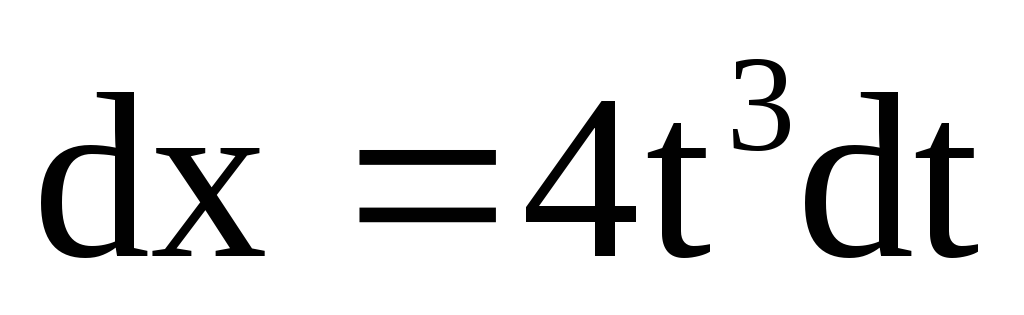. Пусть , тогда , значит . Следовательно,

.

8. Пусть , тогда и , значит . Пусть , тогда , следовательно, .

9. Представим дробное выражение в виде суммы дробей:

. Приведя дроби к общему знаменателю, . Приводя подобные слагаемые, получаем систему уравнений:

.

Таким образом, получаем , значит

.

Найдем каждое слагаемое. Для первого интеграла сделаем замену , тогда , значит . Для второго интеграла сделаем замену , тогда , значит .

Для третьего интеграла сделаем замену , тогда , значит

. Для четвертого интеграла сделаем замену , тогда , значит .

Итак, .

Задание 2.

Вычислить определенные интегралы:

;

Решение:

1. Пусть , , тогда , . Используя формулу интегрирования по частям, получим:

.

2. Сначала преобразуем выражение с помощью тригонометрических формул: . Теперь найдем интеграл

.

Задание 3.

Вычислить несобственные интегралы или установить их расходимость:

;

Решение:

1. 

.

При , тогда .

2. Заметим, что в точке х=0 функция имеет бесконечный разрыв; тогда

. Следовательно, интеграл расходится.

Задание 4.

Выяснить сходимость несобственных интегралов:

;

Решение:

1. Преобразуем подынтегральную функцию 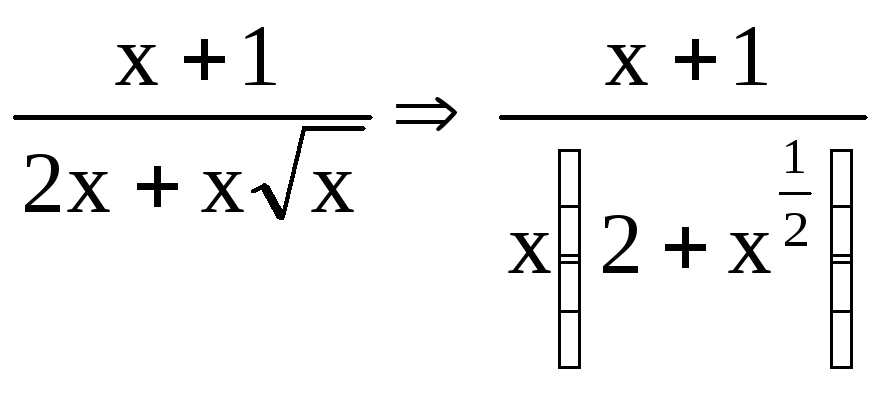. Находя порядок малости подынтегральной функции относительно функции , получаем:

Таким образом, порядок малости подынтегральной функции относительно функции равен 1,5 и, следовательно, интеграл сходится.

2. Подынтегральная функция имеет особенность в точке х=0. Находя порядок роста подынтегральной функции относительно функции , имеем:

Таким образом, порядок роста равен 1 и, следовательно, интеграл расходится.

Задание 5

Найти площадь области, ограниченной линиями , .

Решение:

Сначала построим искомую фигуру. Графиком функции является парабола с вершиной в точке (0;2), ветви параболы направлены вниз. Графиком функции является парабола с вершиной в точке (0;-2), ветви параболы направлены вверх. Найдем точки пересечения графиков функций, решив систему уравнений: , значит, графики функции пересекаются в точках и

EMBED Excel.Sheet.8

Найдем площадь полученной области:

(кв.ед.).

Задание 6

Найти длину дуги кривой , где .

Решение:

Длину дуги кривой найдем по формуле: .

Найдем , тогда . Значит,

.

Рецензия

на контрольную работу № 5

по высшей математике

В задаче 14 неверно найден порядок малости подынтегральной функции.

В задаче 16 ошибки счета.

Переделать задачу 14. Остальные задачи зачтены, их можно не присылать.

Работа не зачтена