1. Новые контрольные / Основы социального прогнозирования
.docx
Контрольная работа № 2
Вариант № 5
по дисциплине «Основы социального прогнозирования»
выполнена по методике Лепихина З. П. «Основы социального прогнозирования»
Задание 1.
Укажите максимально возможное число шагов в агломеративной иерархической классификации.
Решение
В агломеративно-иерархических алгоритмах
процесс объединения объектов в группы
совершается последовательно за
шагов (если объединяются все
объектов).
В отличие от иерархических алгоритмов
в последовательных процедурах на каждом
шаге обрабатывается одно наблюдение.
И если надо разбить n
объектов на
классов, то максимальное число итераций
равно n-k.
Затем каждый из n объектов
относится к одному из k
классов.
Задание 2.
Даны 6 точек в двумерном признаковом пространстве:
|
Объекты |
A |
B |
C |
D |
E |
F |
|
признак-X |
2 |
2 |
1 |
4 |
3 |
1 |
|
признак-Y |
0 |
–1 |
0 |
0 |
0 |
–1 |
Провести классификацию объектов на два класса при помощи алгоритма «дальнего соседа». Построить дендрограмму. Отобразить на плоскости полученный вариант классификации.
Решение
Воспользуемся агломеративным иерархическим алгоритмом классификации. В качестве расстояния между объектами примем обычное евклидово расстояние:
.
Находим попарно расстояния между всеми объектами:
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
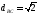В итоге получаем матрицу расстояний между объектами:
.
Шаг 1:
Из матрицы расстояний
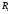следует, что объекты D и
E наиболее близки т.к.
.
Т.е. объекты D и E
объединяются в один кластер.
После объединения имеем 5 кластеров: A, B, C, DE, F.
Расстояния между кластерами находятся
по принципу «дальнего соседа»:
.
В итоге получаем новую матрицу:
.
Шаг 2:
Из матрицы расстояний
следует, что объекты C и
F наиболее близки т.к.
.
Т.е. объекты C и F
объединяются в один кластер.
После объединения имеем 4 кластера: A, B, CF, DE.
В итоге получаем новую матрицу:
.
Шаг 3:
Из матрицы расстояний
следует, что объекты A и
B наиболее близки т.к.
.
Т.е. объекты A и B
объединяются в один кластер.
После объединения имеем 3 кластера: AB, CF, DE.
В итоге получаем новую матрицу:
.
Шаг 4:
Из матрицы расстояний
следует, что объекты AB и
CF наиболее близки т.к.
.
Т.е. объекты AB и CF
объединяются в один кластер.
После объединения имеем 3 кластера: ABCF, DE.
В итоге получаем новую матрицу:
.
Таким образом, расстояние между
полученными кластерами равно:
- по принципу «дальнего соседа».
Представим результаты иерархической классификации объектов в виде дендрограммы.
Задание 3.
По данной выше таблице провести классификацию объектов на 2 класса методом К-средних. Провести максимальное число итераций. В качестве эталонных точек принять точки А и В, порядок появления точек задать самостоятельно. Отобразить на плоскости полученный вариант классификации.
Решение
Максимальное число итераций равно: n-k=6-2=4
1 этап.
Так как в качестве эталонных точек
принимаем точки A и B,
то полагаем нулевое приближение:
.
Шаг 1:
Рассмотрим точку C. Найдем расстояние от точки C до эталонов:
,
.
Т.к.
,
то заменяем эталон
на новый эталон по формулам:
;
.
Т.е.
.
Шаг 2:
Рассмотрим точку D:
.
.
Заменяем эталон
на новый эталон:
.
;
.
Шаг 3:
Рассмотрим точку E:
.
.
Заменяем эталон
на новый эталон:
.
;
.
Шаг 4:
Рассмотрим точку F:
.
.
Заменяем эталон
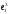на новый эталон:
;
.
.
Т.е. получили два эталона:
;
.
2 этап.
Разобьем все объекты на два класса:
Точка A:
.
точку A включаем в класс,
образованный
.
Точка B:
.
точку B включаем в класс,
образованный
.
Точка C:
.
точку C включаем в класс,
образованный
.
Точка D:
.
точку D включаем в класс,
образованный
.
Точка E:
.
точку E включаем в класс,
образованный
.
Точка F:
.
точку F включаем в класс,
образованный
.
В итоге имеем два класса:
.