Министерство образования и науки

Томский Государственный Университет Систем Управления и Радиоэлектроники (ТУСУР)

Контрольная работа №2

по дисциплине Высшая математика-1

учебное пособие: Магазинников Л.И., Магазинников А.Л. «Высшая математика. Линейная алгебра и

аналитическая геометрия.»

Вариант №13

Выполнил студент

Гр. з-361-а

специальности 210100

Шумаков Роман Александрович

14.02.2012

г. Норильск 2012

1.(С03.РП) Составить общее уравнение прямой, проходящей через точку перпендикулярно прямой .

Решение.

В качестве вектора нормали прямой, примем вектор перпендикулярный вектору N1 (3; -2), например N2 (2, 3).

Уравнение примет вид:

2х + 3y – (2*7 + 3*4)= 0

2х + 3y – 26 = 0

Ответ: искомое уравнение прямой имеет вид 2х + 3y – 26 = 0.

2.(8Т3.РП) Составить общее уравнение прямой, проходящей через точку и точку пересечения прямых и .

Решение.

Уравнение будет иметь вид:

2х + 5y – 8 +*(x – 3y + 4) = 0

Подставим в уравнение координаты точки А(4;3):

2 * 4 + 5 * 3 – 8 + *(4 – 3 * 3 + 4) = 0;

8 + 15 – 8 +*(4 – 9 + 4);

15 - = 0;

Полученное значение подставим в уравнение, получим:

2х + 5y – 8 + 15*(x – 3y + 4) = 0;

2х + 5y – 8 + 15x – 45y + 60 = 0;

17x – 40y + 52 = 0.

Ответ: общее уравнение прямой будет иметь вид: 17x – 40y + 52 = 0.

3.(Т43.РП) Написать общее уравнение плоскости, проходящей через точки , перпендикулярно плоскости .

Решение.

Искомая плоскость параллельна вектору L1(1; -3; 5) нормали данной плоскости L2 = M1M2 = (-3; 4; -5), поэтому вектор нормали N искомой плоскости находится из условия:

N = [L1,L2] =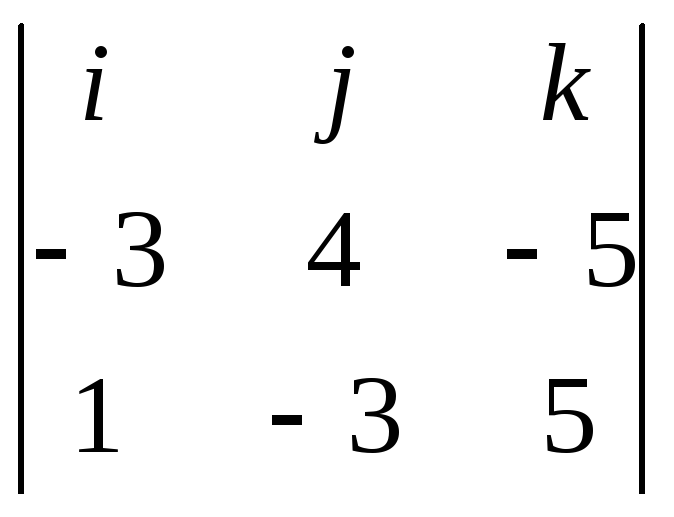= 9k+20i–5j–15i–4k+15j=5i+10j+5k=i+2j +k(1,2,1).

Записываем уравнение плоскости:

х + 2y + z + D = 0

Так как плоскость проходит через точку М1 или М2, то 4+2*(-3)+3+D=0; D=-1

Отсюда:

1 + 2 – 2 + D = 0.

Получили уравнение х + 2у + z – 1= 0

Ответ: х + 2у + z – 1= 0.

4.(303) Найти расстояние от точки до прямой .

Решение.

Найдем расстояние от точки А до прямой по следующей формуле:

d =

d =

Ответ: расстояние от точки А до прямой d=3.

5.(5Б3.РП) Найти те значения параметров и , при которых прямые и параллельны.

Решение.

Найдем направляющий вектор для первой и второй прямой.

Для их вычисления будем использовать формулу:

1) (1 прямая)

2) (2 прямая)

Т.к. АВ, получим систему уравнений:

;

Ответ: А=0, В=-1

6.(733) Прямая параллельна плоскости , пересекает прямую и проходит через точку . Найти ординату точки пересечения прямой с плоскостью .

Решение.

Т.к. прямая проходит через точку А (3, -2, -4), то уравнение L будет иметь вид:

;

Далее найдем значения m,n,k. Используя условие параллельности прямой и плоскости имеем:

Запишем уравнение плоскости:

, пусть:;;;; Тогда:

;

, где m=

Полученное значение подставим в уравнение L:

Найдем ординату точки пересечения прямой с плоскостью

; ;

;

;

.

Подставим значения x,y,z в уравнение: x+y+z-9=0

;

;

;

-8t=72; t=-9

Ордината точки пересечения прямой с плоскостью: y=-9-2=-11

Ответ: -11.

7.(983). Найти радиус окружности, имеющей центр в точке , если она касается прямой .

Решение.

Найдем радиус окружности. Для этого найдем расстояние от точки А до прямой по следующей формуле:

;

Ответ: радиус окружности равен 6.

8. Дана кривая .

8.1. Доказать, что данная кривая – эллипс.

8.2.(ТТ3.РП) Найти координаты центра его симметрии.

8.3.(4Б3.РП) Найти его большую и малую полуоси кривой.

8.4.(2П3) Записать уравнение фокальной оси.

8.5. Построить данную кривую.

8.1.Каноническое уравнение эллипса следующее:

Выделим полные квадраты:

;

;

.

Приведем к каноническому виду:

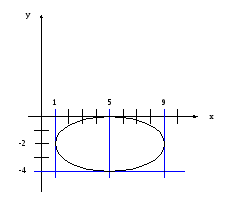
8.2.Находим координаты центра симметрии: х=5; у=-2;

8.3.Большая полуось равна 4, малая 2;

8.4.Фокальная ось равна х=5.

8.5.

9. Дана кривая .

9.1. Доказать, что данная кривая – парабола.

9.2.(Л33). Найти значение её параметра .

9.3.(2Т3.РП). Найти координаты её вершины.

9.4.(7Б3). Написать уравнение её оси симметрии.

9.5. Построить данную кривую.

Решение.

9.1.Преобразуем уравнение:

;

;

Уравнение параболы имеет вид: , следовательно данная кривая является параболой.

9.2.Значение параметра р=-6.

9.3.Координаты вершины (-3;-2)

9.4.Уравнение оси симметрии: х=3

10. Дана кривая .

10.1. Доказать, что данная кривая – гипербола.

10.2.(793.РП). Найти координаты центра её симметрии.

10.3.(8Д3.РП). Найти действительную и мнимую полуоси.

10.4.(ПС3.РП). Написать уравнение фокальной оси.

10.5. Построить данную кривую.

Приведем уравнение в квадратичную форму:

,

Квадратичную форму приводим к главным осям. Для этого запишем матрицу этой квадратичной формы:

и находим корни характеристического уравнения матрицы В:

;

Т.к. собственные числа имеют разные знаки, то данное уравнение определяет кривую гиперболического вида. Найдем собственные векторы матрицы В. Для получим систему:

;

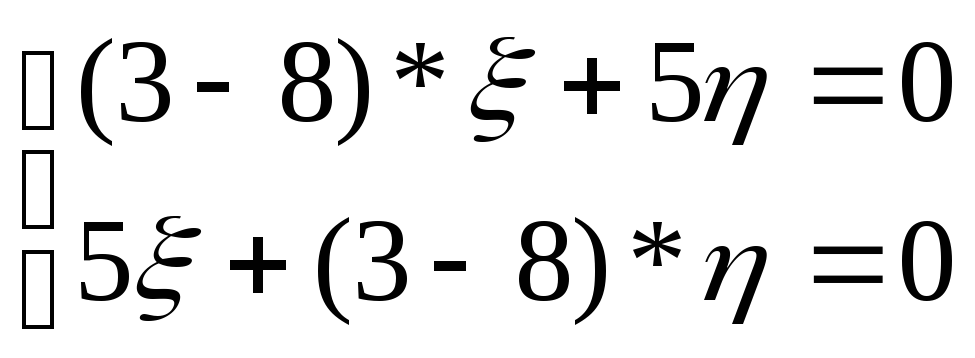Полагая что , то собственный вектор матрицы В равен (1,1)

Найдем единичный собственный вектор . По свойству собственных векторов симметрического оператора второй собственный вектор ортогонален вектору . Выберем вектор таким образом, чтобы базис был правым. От старого базиса перейдем к новому базису .Матрица перехода имеет вид:

, . Старые координаты (х,у) связаны с новыми соотношениями ,, или

Уравнение примет следующий вид:

или

Выделяя полные квадраты, получим:

(мнимая полуось)

(действительная полуось)

Произведем преобразование параллельного переноса системы координат в новое начало :

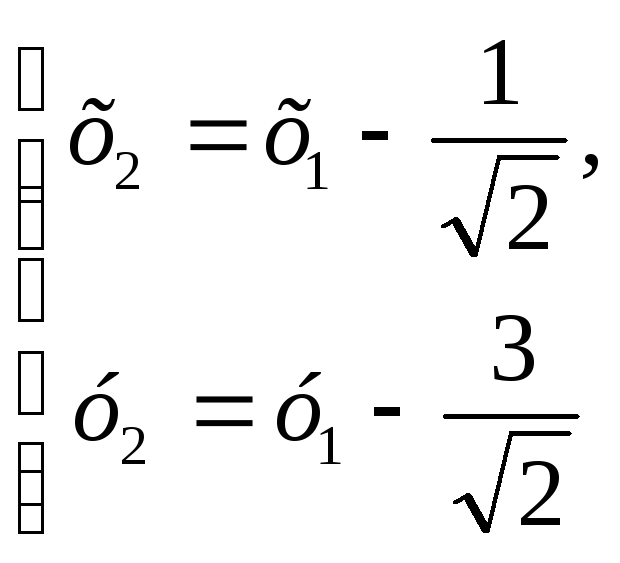или теперь

В системе координат (О₁, i₁, j₁) гипербола имеет уравнение:

Оси О₁х₂, О₁у₂ направлены по прямой , .

Координаты точки О₁, являющейся центром симметрии гиперболы, находим, решая систему: , получаем х=-1, у=2, О₁(-1,2). Фокальной осью является прямая у₂ =0, . Для построение гиперболы строим в старой системе новую систему, в которой строим данную гиперболу. Заметим, что прямые у₂ = + 2х₂ являются её асимптотами.