РТЦиС контрольная

Контрольная работа

РТЦ и С

Вариант 073

ИСХОДНЫЕ ДАННЫЕ

Длительность импульса: мкс.

Частота следования периодического сигнала: кГц.

Период сигнала мкс.

Амплитуда импульса: В.

Временные свойства сигнала: , , , .

Постоянная времени линейной цепи: ,.

Рис.1 – Дифференцирующая цепь

Рис.2 – Интегрирующая цепь

1.1. Выполнить математическое описание заданного периодического сигнала, изобразить графически два-три периода сигнала, указав на рисунке параметры, характеризующие сигнал.

Рис.3 – Временное представление сигнала

Периодический сигнал представляет собой знакочередующуюся последовательность импульсов прямоугольной формы. Математическое описание проведем, используя графическую модель сигнала, изображенную на рис.3.

Скважность, определяемая отношением периода сигнала к длительности прямоугольного импульса, равна:

.

Временные свойства сигнала на рис.3:

нечетная симметрия относительно t = 0

,

четная симметрия относительно t = Т/4

.

2.1. Расчет прохождения периодического и непериодического сигналов, состоящих из прямоугольных импульсов, через интегрирующие и дифференцирующие RC-цепи.

2.1.1. Рассчитать и построить в масштабе АЧХ и ФЧХ интегрирующей и дифференцирующей цепей в диапазоне от нуля до .

Указание: по шкале абсцисс сделать градуировку частоты в кГц и в безразмерных величинах .

Дифференцирующая цепь

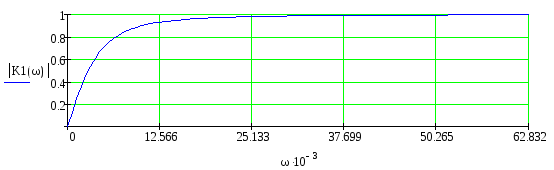
Рис.4 – АЧХ

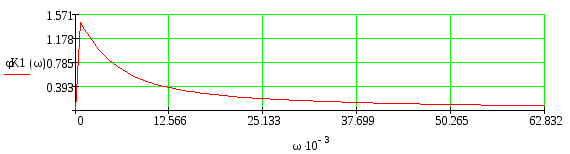
Рис.5 – ФЧХ

Интегрирующая цепь

Рис.6 – АЧХ

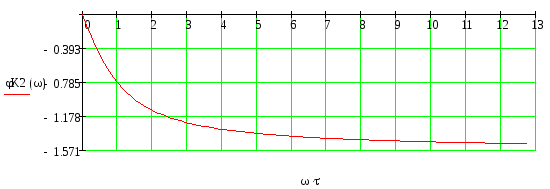
Рис.7 – ФЧХ

2.1.2. Рассчитать и построить в масштабе переходную и импульсную характеристики цепей от нуля до (мкс).

Указание: по шкале абсцисс сделать градуировку времени в мкс и в безразмерных величинах .

Дифференцирующая цепь

Рис.8 – Переходная характеристика

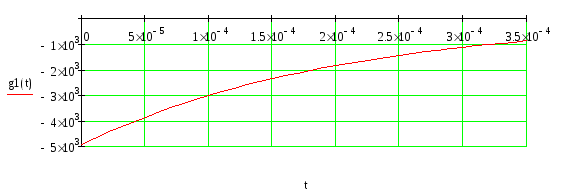
Рис.9 – Импульсная характеристика

Интегрирующая цепь

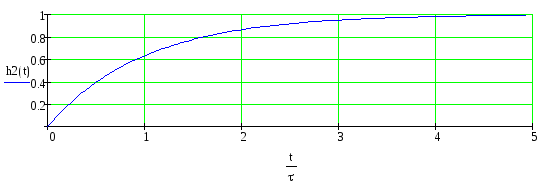
Рис.10 – Переходная характеристика

Рис.11 – Импульсная характеристика

2.1.3. Проверить выполнение предельных соотношений между частотными и временными характеристиками.

Для дифференцирующей цепи: Для интегрирующей цепи:

, ,

, ,

2.1.4. Рассчитать спектры амплитуд и фаз на выходе заданных цепей при действии периодического сигнала s₁(t).

Анализируя временное представление сигнала, видим:

-  сигнал является нечетной функцией времени;

-сигнал представляет собой знакочередующуюся последовательность импульсов, и в этом случае постоянная составляющая равна нулю:

.

На основании изложенных свойств предполагаем, что в разложении сигнала будут присутствовать только синусоидальные элементарные гармонические составляющие, то есть

, , .

И, следовательно, ряд Фурье можно преобразовать следующим образом:

.

Проведем расчет весовых коэффициентов , используя при этом формулу

.

Для проведения дальнейших упрощений воспользуемся очевидными соотношениями

 .

.

Систематизируем полученные выражения

,, ; ;

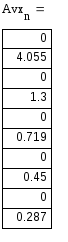
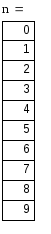
Таблица 1 – Спектры амплитуд и фаз

	0	1	2	3	4	5	6	7	8	9
		0	0	0	0	0	0	0	0	0
		4.055	0	1.3	0	0.719	0	0.45	0	0.287
		4.055	0	1.3	0	0.719	0	0.45	0	0.287
		-0.5		-0.5		-0.5		-0.5		-0.5

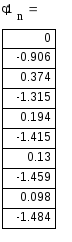
2.1.5. Построить с учетом масштаба на общих спектрограммах для каждой цепи спектры амплитуд и фаз входного и выходного сигналов при действии на цепь сигнала s₁(t).

Дифференцирующая цепь

Рис.12 – Спектр амплитуд

Рис.13 – Спектр фаз

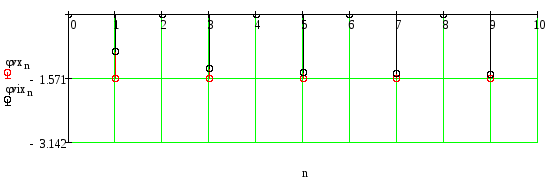
Интегрирующая цепь

Рис.14 – Спектр амплитуд

Рис.15 – Спектр фаз

2.1.6. Дать динамическое представление входного сигнала s₂(t).

Интервал времени

Входной сигнал

2.1.7. Получить динамическое представление отклика заданных цепей на действие сигнала s₂(t).

Интервал времени

Отклик

2.1.8. Изобразить отклики интегрирующей и дифференцирующей цепей на интервале времени от нуля до t_max, в три раза превышающем длительность воздействия s₂(t) (воздействие и соответствующий отклик цепи изображать на общем рисунке).

Дифференцирующая цепь

Рис.16 – Отклик цепи

Интегрирующая цепь

Рис.17 – Отклик цепи

2.1.9. Сделать выводы по результатам проведенного анализа.

Построены и рассчитаны – АЧХ, ФЧХ, переходная и импульсная характеристики. Построены спектрограммы амплитуд и фаз выходных сигналов. Изобразили отклики на входной сигнал интегрирующей и дифференцирующей цепей.

15