ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ

(ТУСУР)

Заочный факультет (дистанционная форма обучения)

Кафедра автоматизированных систем управления (АСУ)

Математическая экономика

Лабораторная работа № 4

Вариант 20

Студент Авдеева Екатерина Сергеевна

Дата выполнения работы _ _

Дата проверки _ _

Оценка _ _

И. О. Фамилия преподователя _ _

Подпись преподователя _ _

Мирный

2008 г.

1. Задача

1. Вычислить матрицу , где

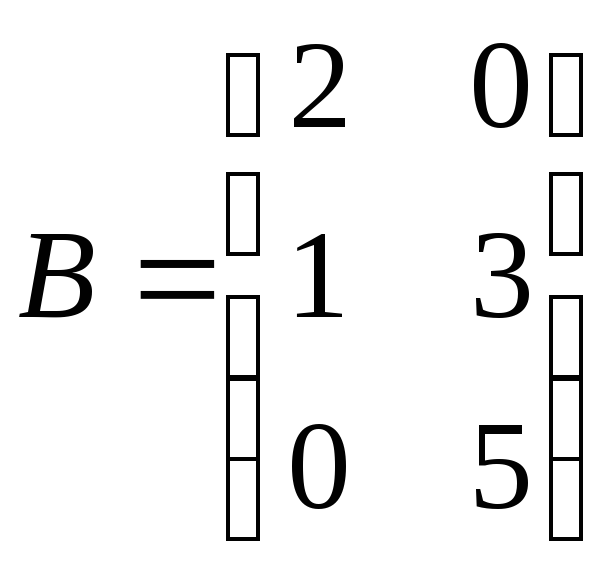
Решение:

Зададим исходные матрицы:

Так как матрица А не является квадратной, то возвести ее в степень невозможно. Зададим формулу вычисления матрицы D и получим результат:

2. Задача

Вычислить определитель матрицы

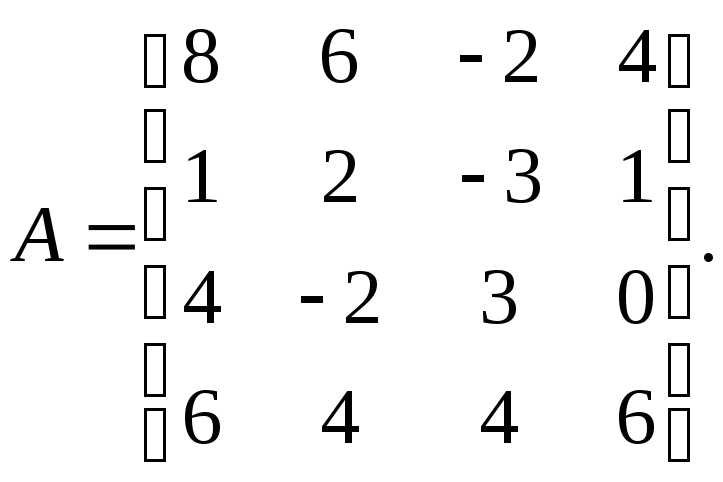
Решение:

3. Задача

Решить систему уравнений

Решение:

Зададим матрицу коэффициентов при неизвестных и вектор свободных членов:

Используя встроенную функцию lsolve, найдем неизвестные:

4. Задача

Решить матричное уравнение , если

; ; .

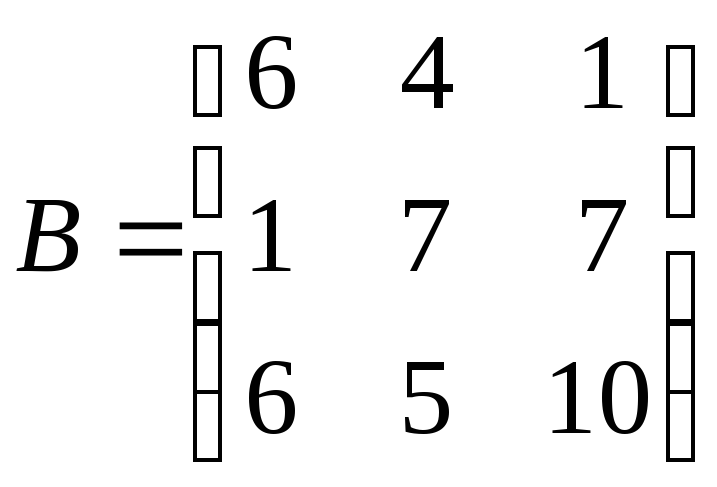Решение:

Задаем матрицы:

Выразим искомую матрицу X из заданного уравнения.

Х = А ^-1 * С * В ^-1.

5. Задача

С двух заводов поставляются автомобили для двух автохозяйств. Первый завод выпустил 700 машин, а второй – 300 ма­шин. Затраты 1 автохозяйства на перевозку автомобилей составили 3800 у.д.е., затраты 2 автохозяйства составили 15000 у.д.е. Известны затраты на перевозку одного автомобиля с завода в каждое автохозяйство (см. таблицу).

Завод	Затраты на перевозку в автохозяйство, ден. ед.
	1	2
1	15	20
2	8	25

Найти план перевозок машин и общую стоимость перевозок

Решение:

Неизвестными задачи являются объемы перевозок от каждого завода каждому автохозяйству. Целевая функция задачи равна сумме затрат на все перевозки. Она должна достигать минимального значения.

Z(х) = 15х11 + 20х12 + 8х21 + 25х22 min

Ограничения:

х11 + х12 700

х21 + х22 300

15х11 + 8х21 3800

20х12 + 25х22 15000

хij 0

Используем метод минимальной стоимости. Среди элементов матрицы стоимостей выбираем наименьшую стоимость с12 = 8. В эту клетку запишем максимально возможную перевозку.

	3800	15000
700	15	20
300	8	25

	3800	15000
700	15 1400 (93)	20 12140 (607)
300	8 2400 (300)	25

Затраты первого автохозяйства уменьшаем на 2400. Исключаем из рассмотрения второй завод, так как его запросы удовлетворены. В матрице вычеркиваем вторую строку. В оставшейся части матрицы наименьшей является стоимость с11 = 15. Максимальная перевозка равна 1400. Определяем оставшиеся запасы первого завода 700-93 = 607.

Общая стоимость перевозок:

15 * 93 + 20 * 607 + 8 * 300 = 15935 у.д.е.

Примечание:

Задание 5 не могу сделать в MathCAD, решила обычным способом как могла