1. Новые контрольные / Дифференциальное исчисление. К.р. 2. Вариант 6
.docЗадания. Дифференциальное исчисление. К.р. 4. Вариант 6. Магазинников
Решения.
-
по правилу нахождения производной имеем:
а)
Находим производную в точке х=1:
.
Б)
При
имеем tg(x)=1,
cos(x)=1/
,
поэтому
В)
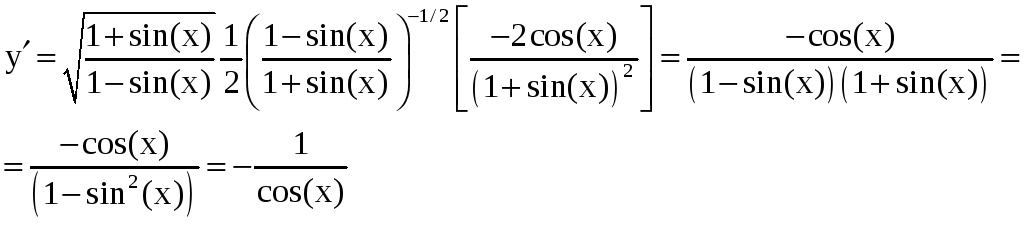
Здесь легко видеть, что
-
находим производные :
.
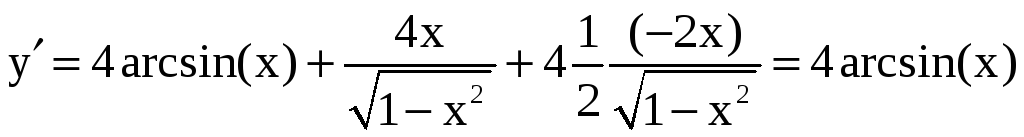тогда вторая производная равна
Соответственно значение в точке (3/5):
-
Найти первых 2 производных функции
и найти их значения в точке х=1.
Решение.
Ищем первую и вторую производную функции:
,
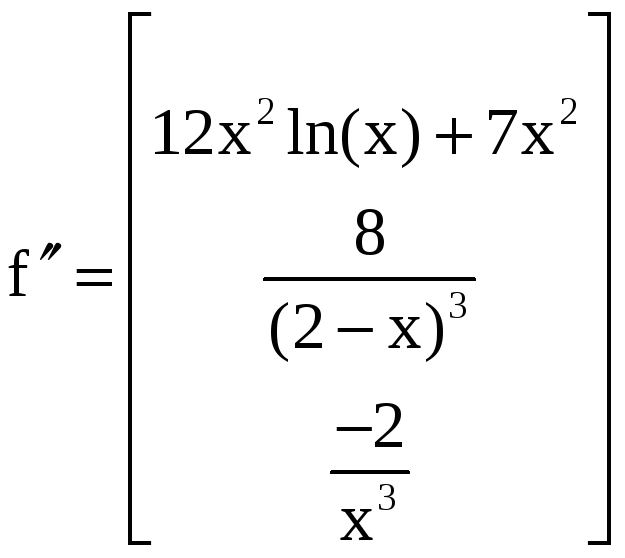
Теперь найдем значения производных в точке х=1:
,
.
-
показать что функция
удовлетворяет уравнению
Найдем первые производные:
,
и далее вторые производные:
Таким образом, подставляя в исходное уравнение, получим:
что
и требовалось показать.
5. Найти производную функции
Решение.
Ищем производную функции двух переменных,
получаем матрицу:
В точке (-3,4) получим:
.
Сумма элементов матрицы равна 5.
-
дана функция
.
а) ищем градиент:
Его координаты в точке М(1, 0.2, 3), очевидно,
будут
.
Б) производная по направлению есть:
.
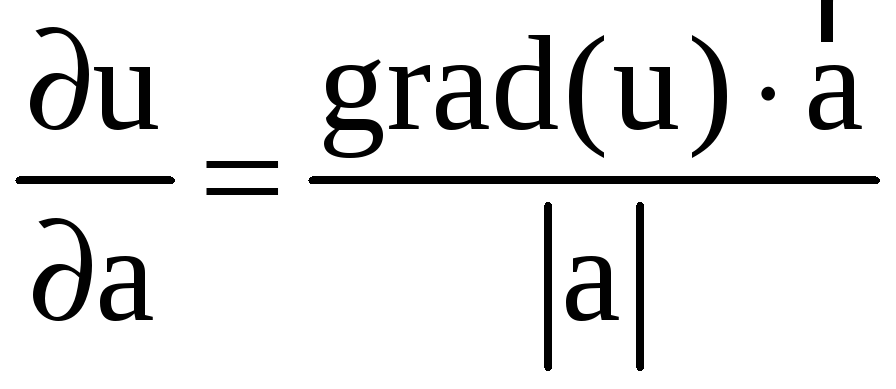Поскольку
,
получаем:
Ответ: а)
,
б) -1.
-
найти
,
если
.
Находить вторую производную параметрически заданной функции будет по правилу:
Найдем первые производные по параметру t:
.
Тогда
Находим производную
:
Тогда искомая производная есть
.
Найдем значение
:
Ответ:
,
.
-
Дано
.
Найти
и
.
Решение.
Используем формулы:
.
Поскольку
,
и
,
получим
,
.
Ответ: 0, 0 .
-
В точке х=0 к графику
проведена касательная. Найти абсциссу
точки касательной с у=19.
Решение.
В точке х=0 ордината равна
.
Поскольку общее уравнение касательной
к графику
в точке (х0, у0) имеет вид
,
находим производную
и далее уравнение касательной в виде
.
Отсюда искомая абсцисса
Ответ: 9.
10. Найти dy если
.
При х=1 и dx=0.024 получим
Ответ:
.
-
Дано
.
Найти
при переходе из точки М0(2, 4) в точку
М1(1,98; 3,91).
Решение
По определению
.
Представляя
,
где
и х=2, у=4, получим
.
В свою очередь
.
Частные производные равны
,
так что
.
Ответ:
.
12. дано
.
Найти ее макс. и миним. значение на
отрезке [-1, 5].
Решение.
Найдем точки экстремума внутри отрезка. Ищем производную функции:
Приравнивая ее нулю, найдем совпадающий
с концом отрезка корень х=5, те это точка
экстремума. В этой точке значение функции
.
Далее найдем вторую производную, и,
приравнивая ее нулю, получим точки
перегиба х=1, которая попадает в интервал
[-1, 5] и
,
которые не попадают в интервал.
В точке перегиба х=1 получаем у(1)=1.
Также найдем значение функции на конце отрезка у(-1)=-3.
Таким образом, минимальное значение функции равно -3, а максимальное 1.
13. найти максимум и минимум функции
в круге
.
Решение.
Рассмотрим функцию на границе - окружности и внутри круга.
На границе
,
так что
.
Найдем точки экстремума функции одной
переменной х:
,
откуда
,
так что соответствующие значения функции
.
Рассмотрим далее функцию z внутри круга.
Найдем первые частные производные:
Приравнивая их нулю, найдем точку условного экстремума (0, 0).
Для выяснения типа точки ищем вторые производные, обозначив их буквами:
Далее составим величину
,
как видно она не зависит от координат
и равна -1. Это значит, что точек экстремума
внутри круга нет. Следовательно, максимум
и минимум функции находятся на окружности,
и равны +2 и -2 соответственно.
14. Построить график функции
.
1. область определения
.
2. область значения
.
3. точка х=0 - точка разрыва.
4. точка пересечения с осью х - х=1, ось у не пересекает.
5. функция ни четная, ни нечетная.
6. ищем точки экстремума
,
откуда
.
На участке
функция возрастает, так как производная
больше нуля, а на остальном интервале
убывает.
Найдем вторую производную:
для любых конечных х, те точек перегиба
нет.
Вторая производная положительная, поэтому везде функция вогнутая.
7. Асимптоты:
8. Очевидно, есть вертикальная асимптота х=0, горизонтальной нет, поскольку
.
Ищем, есть ли наклонная асимптота вида
.
По определению
,
а
.
Таким образом есть наклонная асимптота у=-х.
Объединяя всю информацию, строим график (зеленым показана наклонная асимптота):
