
gos_янв_2009 / 2.3. МО
.doc|
1. Основные понятия и определения. Задача оптимизации общего вида. Целевая функция, ограничения. Оптимальное решение. Точность. Математическое программирование в самом общем виде можно определить как задачу оптимизации с ограничениями в пространстве Rn: min
f(x),
gk(x)
= 0,
Вектор xD имеет компоненты x1, x2, … xn, которые являются неизвестными задачи. Функция f(x) называется целевой функцией (ЦФ) (функцией качества, критерием оптимальности), а множество условий gk(x), lj(x) и xD – ограничениями задачи. Решением задачи называют любой вектор x, удовлетворяющий ограничениям. Оптимальным решением или глобальным экстремумом задачи называют вектор x*, минимизирующий значение f(x) на множестве всех решений: f(x*) f(x) для всех x D. Задача максимизации функции сводится к задаче поиска минимума функции F = - f(x). Точность. Характеристикой точности полученного решения может служить величина абсолютного отклонения значения минимизируемой функции, достигнутого в точке xn D, от точного значения ее минимума на множестве D: (x)
= Ясно, что чем меньше неотрицательная величина , тем точнее полученное решение. Недостатком использования абсолютной погрешности является то обстоятельство, что она меняется при умножении ЦФ на положительную константу : f (x) f (x). Целесообразнее использовать следующую оценку точности:
|
2. Основные этапы постановки и решения задачи оптимизации. Для того чтобы использовать математические результаты и численные методы теории оптимизации для решения конкретных инженерных задач, необходимо:
Корректная постановка задачи служит ключом к успеху оптимизационного исследования. Искусство постановки задачи постигается в практической деятельности на примерах успешно реализованных алгоритмов и основывается на четком представлении преимуществ, недостатков и специфических особенностей различных методов оптимизации. Значительный интерес представляет деление задач оптимизации по виду целевой функции и ограничений, поскольку специфические особенности тех или иных задач играют важную роль при разработке методов и их решений.
|
|
3. Классификация задач оптимизации по виду целевой функции и ограничений. Значительный интерес представляет деление задач оптимизации по виду целевой функции и ограничений, поскольку специфические особенности тех или иных задач играют важную роль при разработке методов и их решений. Задача
оптимизации с одной переменной: min
f
(x),
xR1,
ограничения отсутствуют, т.е. в задаче
gk(x)
= 0,
Задача оптимизации без ограничений (безусловная оптимизация): min f(x), xRn, k = j = 0, xi[- , + ]. Задача
оптимизации с ограничениями
(условная
оптимизация): min
f(x), gk(x)
= 0, k
= 1, K;
lj(x)
> 0, j
= 1, J;
Задача
условной оптимизации с линейными
ограничениями.
Функции–ограничения
gk
и lj
в задаче min
f(x),
gk(x)
= 0, k
= 1, K;
lj(x)
> 0, j
= 1, J;
являются линейными, а целевая функция может быть либо линейной, либо нелинейной. Задача
линейного программирования
(ЛП):
Задача целочисленного программирования: В задаче ЛП компоненты вектора х принимают только целые значения. Задача нелинейного программирования с линейными ограничениями: Целевая функция f(x) – нелинейная, а все ограничения – линейные функции. Оптимизационные задачи такого рода можно классифицировать на основе структурных особенностей нелинейных целевых функций. Задача
квадратичного программирования:
Найти
минимум f(x),
где целевая функция f(x)
является квадратичной.
Задача
дробно-линейного программирования:
Целевая
функция есть отношение линейных
функций:
|
4. Унимодальные функции. Критерии для проверки унимодальности. Многие методы оптимизации применимы только тогда, когда целевая функция f(x) является унимодальной, т. е. любой локальный минимум ЦФ одновременно является и глобальным. Множество функций, унимодальных на отрезке [a, b], обозначим Q[a, b]. Для проверки унимодальности функции f(x) на практике используют следующие критерии: – если функция f(x) дифференцируема на отрезке [a, b] и производная f'(x) не убывает на этом отрезке, то f (x) Q [a, b]; – если функция f(x) дважды дифференцируема на отрезке [a, b] и вторая производная f''(x)≥0 при х [a, b], то f(x) Q[a, b]. Если эти критерии не выполняются, то функция f(x) является мультимодальной или многоэкстремальной.
|
|
5. Выпуклые множества и функции. Функция f(x) выпукла на [a, b], если справедливо неравенство Иенссена:
для произвольных х1 и х2 [a, b] и μ [0, 1]. На практике обычно используют следующие критерии: одномерный случай: 1) дважды дифференцируемая функция f(x) выпукла на [a, b], если вторая производная f " (x) ≥ 0 при всех х [a, b]; многомерный случай (критерий Сильвестра): 2) если функция f(x) дважды дифференцируема на выпуклом множестве D Rn и все угловые миноры матрицы Гессе – матрицы вторых производных Hf(x) = ∂2f(x) / (∂xi ∂xj) – положительны при хD, то функция f(x) выпукла на множестве D.
|
6. Квадратичные формы. Критерии определенности квадратичных форм (теорема Сильвестра). Во
многих задачах оптимизации рассматриваются
функции вида:
или
в матричном виде:
Градиент и матрица Гессе этой функции равны соответственно grad f(x) = Ax + b, Hf(x) = A = (a i j). Таким образом, для того чтобы функция была выпуклой в Rn, достаточно, чтобы матрица А была положительно определена. Критерии определенности матрицы (теорема Сильвестра). Положительная определенность:
Положительная полуопределенность:
Главный определитель – это определитель главного минора. Для
положительной определенности
квадратичной формы – матрицы А
–
необходимо и достаточно, чтобы все
угловые миноры матрицы А
были положительны, т. е.
Стационарной
точкой
функции f(x)
называется такая точка x*,
в которой выполняется равенство Если стационарная точка не соответствует локальному экстремуму, то она является точкой перегиба или седловой точкой.
|
|
7. Необходимые и достаточные условия существования экстремума: скалярный случай; векторный случай; минимизация при ограничениях. Скалярный случай xr1 Если
в точке x*
первые (n
- 1) производные функции f(x)
обращаются в нуль, а производная
порядка n отлична от нуля, т.е.
1) если n – нечетное, то x* – точка перегиба; 2) если n – четное, то x* – локальный экстремум; причем, если
Примечание. При поиске глобального минимума функции f(x), заданной на отрезке [a, b], необходимо найти все точки локальных минимумов, вычислить в них значения функции, а также вычислить значения функции на границах отрезка f(a) и f(b) и выбрать среди этих значений наименьшее. Векторный случай Функция f(x) имеет в точке x* локальный минимум, если выполняется равенство: grad f(x*) = 0, т. е. x* - стационарная точка, и матрица Гессе H f(x*) положительно определена. Для выпуклых функций найденный локальный минимум будет являться одновременно и глобальным. Минимизация при ограничениях Рассматривается
задача:
Здесь все функции f, gk, L предполагаются непрерывно дифференцируемыми. Точка
x*
будет
глобальным
экстремумом
задачи, если в точке x*
выполняются условия
Куна-Таккера:
существует такое *
0, что grad
L(
x,
*)
= 0; *
gk(x)
= 0; k
=
Пара векторов (x*, *) образует седловую точку функции Лагранжа, если при всех x D и 0 выполняется неравенство: L(x*, ) L(x*, *) L( x, *). Таким образом, точка x* является точкой глобального минимума задачи, если пара векторов (x*, *) является седловой точкой функции L( x, ).
|
8. Основные характеристики алгоритмов оптимизации. Сходимость алгоритма является наиболее важным вопросом оптимизации. Большинство методов решения ЗО имеют итерационную природу: xi+1 = A (xi), т. е. Исходя из некоторой начальной точки x0, они порождают последовательность { x0, x1, …, xi, …} на основе алгоритма A, сходящуюся к точке экстремума x*. Априорные характеристики методов: трудоемкость вычислений, скорость сходимости, устойчивость метода к ошибкам в вычислениях, чувствительность метода к значениям параметров алгоритма и ряд других. Сходимость алгоритма является наиболее важным вопросом оптимизации. Большинство методов решения ЗО имеют итерационную природу: xi+1 = A (xi), т. е. Исходя из некоторой начальной точки x0, они порождают последовательность { x0, x1, …, xi, …} на основе алгоритма A, сходящуюся к точке экстремума x*. Глобальная сходимость. Алгоритм A обладает свойством глобальной сходимости, если для любой начальной точки x0, последовательность {xk}, определяемая выражением xk = A (xk-1), сходится к точке, удовлетворяющей необходимым условиям оптимальности. Данное свойство отражает надежность работы алгоритма. Асимптотическая сходимость и скорость сходимости. С практической точки зрения эффективность алгоритма зависит от числа итераций, необходимых для получения приближенного решения x* с заданной точностью . Для получения критерия с некоторым абсолютным значением необходимо прибегнуть к другому типу анализа, взяв за объект исследования асимптотическую сходимость – поведение последовательности точек {xk} в окрестности предельной точки x*. Это значит, что каждому алгоритму приписывается индекс эффективности – скорость сходимости. Линейная
сходимость.
Выполняется неравенство:
Суперлинейная
сходимость:
Сходимость
порядка p.
Если существует такое число p
> 1 (2,3…), что
Исследование скорости сходимости алгоритма позволяет оценить его эффективность и осуществить его сравнение с другими алгоритмами. Для оценки эффективности выбранных методов можно рекомендовать три характеристики: время, затраченное на получение решения; точность решения; чувствительность к изменению параметра сходимости. Для одномерных методов оптимизации первые две характеристики можно исследовать на типовых тестовых функциях, например, f(x) = sin k (x), путем варьирования значений показателя степени k на множестве нечетных чисел от 1 до 79.
|
|
9. Связь методов оптимизации и поиска нулей функции. Критерии останова. Численная аппроксимация градиента. Методы поиска нулей функции Поиск
нулей функции f(x)
широко используется в методах
оптимизации. Например, такая необходимость
возникает при определении стационарной
точки f '
(x)
= 0 или решении системы нелинейных
уравнений f
/ xi
= 0, i
=
Кроме широко известных методов поиска нулей функции можно предложить следующие методы: 1) упрощенный метод Ньютона (сходимость линейная): xi+1 = xi – (xi)/, где – константа, например, = f ' (x0); 2)
метод ложного положения
(сходимость линейная):
3)
метод
Стефенсена
(квадратичная сходимость):
4)
метод Уолла
(кубическая сходимость):
Критерии останова Приведем несколько наиболее распространенных критериев останова оптимизационных методов ( – заданная точность): 1) 4)
max
6)
grad||
f(x)
|| =
где k – четное число (данный критерий используется в методах штрафных и барьерных функций). При выполнении неравенств полагают: x* xk и f* f(xk). Численная аппроксимация градиента. В методах оптимизации с использованием производных аналитическое вычисление производных может быть затруднительно или невозможно. В этом случае производные (компоненты вектора градиента) можно определять на основе численной аппроксимации: 1)
"конечная разность вперед": 2)
"центральная конечная разность":
Выбор
осуществляется в зависимости от вида
функции f(x),
координат точки
|
10. Методы интервальной оценки: дихотомии, золотого сечения, Фибоначчи. Суть методов интервальной оценки заключается в последовательном исключении, интервалов в которых не может содержаться нуль функции. В методе дихтомии исходный отрезок делится пополам, происходит сравнения значения функции на границах отрезка и его в середине. И исключается тот интервал значение функции на границе которого имеет один и тот же знак. В итоге получается с заданной точностью оценка интервала, в котором содержится нуль функции. В методах оптимизации нуль обычно ищется нуль первой производной (градиента) Метод золотого сечечения и Фибоначчи аналогичны методу дихтомии с той разницей, что вместо середины интервала берется точка вычисленная по золотому сечению или числам Фибоначчи. Метод Фибоначчи является предельным случаем метода золотого сечения. PS: Показать метод дихотомии (половинного деления отрезка) с помощью рисунка. |
|
11. Методы полиномиальной аппроксимации. Основная идея рассматриваемых методов связана с возможностью аппроксимации гладкой функции полиномом и последующего использования этого полинома для оценивания координаты точки экстремума. Необходимые условия эффективной реализации такого подхода – унимодальность и непрерывность исследуемой функции. Согласно теореме Вейерштрасса об аппроксимации, если функция непрерывна на некотором интервале, то ее с любой степенью точности можно аппроксимировать полиномом высокого порядка. Координату точки экстремума функции можно оценить путем вычисления координаты точки экстремума полинома. Метод Пауэлла Этот метод основан на последовательном применении процедуры оценивания с использованием квадратичной аппроксимации. Схема
алгоритма Пауэлла:
пусть
Шаг
1: Вычислить
Шаг
2: Вычислить
Шаг
3: Если
Шаг
4: Вычислить
Шаг
5: По трем точкам
Шаг 6: Проверка на окончание поиска: а)
является ли разность
б)
является ли разность
Если условия а) и б) выполняются одновременно, то закончить поиск. Иначе переход на Шаг 7. Шаг
7: Выбрать "наилучшую" точку (
|
12. Методы с использованием производных на примере одного из методов: Коши, Ньютона, Больцано. Необходимым
условием существования локального
минимума функции в некоторой точке
Если
Одним из таких методов является метод средней точки (поиск Больцано) Пусть
Для
нахождения корня уравнения
Если
в точке
Если
в точке
Определим
две точки
Формализованное
описание алгоритма. Пусть задана
функция
Шаг
1: Положить
Шаг
2: Вычислить
Шаг
3: Если
|
|
13. Сравнение эффективности одномерных методов оптимизации. С помощью теоретических выкладок можно показать, что такие методы точного оценивания, как метод Пауэлла, метод поиска с использованием кубичной аппроксимации и производных существенно эффективнее методов исключения интервалов, среди которых выделяется метод золотого сечения. Данный вывод справедлив лишь в предположении, что интервалы сходимости сравнимы между собой, а исследуемая функция является достаточно гладкой и унимодальной.
Для оценки эффективности методов обычно используются три характеристики:
Например,
метод средней точки, метод Пауэлла и
поиск с использованием кубичной
аппроксимации могут быть исследованы
при поиске
При возрастании значения k увеличивается время решения и уменьшается точность. Однако МЗС не чувствителен к росту k.
|
14. Прямые методы безусловной многомерной оптимизации на примере одного из методов: симплекс-метод, Хука-Дживса, сопряженных направлений Пауэлла. Методы прямого поиска (нулевого порядка) основаны на вычислении только значений ЦФ, к ним относятся: поиск по симплексу; метод Хука-Дживса; метод сопряженных направлений Пауэлла и другие. Достоинства данных методов: относительная простота вычислительных процедур, легкость реализации и корректировки. Недостатки: значительные затраты времени по сравнению с градиентными методами. Для примера рассмотрим симплексный метод Метод поиска по симплексу был предложен в 1962 г. Спендли, Хекстом и Химсвортом. Этот метод называют последовательным симплекс-методом (ПСМ). Следует отметить, что указанный метод и другие подобные методы не имеют отношения к симплекс-методу линейного программирования, а сходство названий носит чисто случайный характер. Симплекс-метод Этот метод называют последовательным симплекс-методом (ПСМ). Определение: В к-мерном эвклидовом пространстве, к-мерный симплекс представляет собой фигуру, образованную к+1 точками (вершинами), не принадлежащими одновременно ни одному пространству меньшей размерности. В одномерном пространстве симплекс (С) есть отрезок прямой; в двумерном – треугольник; в трехмерном – треугольная пирамида (тетраэдр) и т.д. Симплекс называется регулярным, если расстояния между вершинами равны. В ПСМ используются регулярные симплекс-планы. Из любого симплекса, отбросив одну его вершину, можно получить новый симплекс, если к оставшимся добавить всего лишь одну точку. Для оценки направления движения во всех вершинах С Vj, j=1, ... , n+1, где n- размерность вектора X, необходимо оценить значение ЦФ fj=f (Vj). При
поиске min наиболее целесообразно будет
движение от вершины Vs с наибольшим
значением fs к противоположной грани
С. Шаг поиска выполняется переходом
из некоторого С. Sm-1 в новый С. Sm путем
исключения вершины Vs и построения ее
зеркального отображения относительно
грани
Алгоритм ПСМ. Определение
координат
производится
с помощью матрицы . (4.6) Здесь j - номер вершины j = 1, ..., n + 1, i – номер координаты i=1,..., n, где
Координата
|
|
15. Градиентные методы оптимизации на примере методов Коши, Ньютона и модифицированного метода Ньютона. Предполагается,
что целевая функция f(x)
непрерывна и имеет, по крайней мере,
непрерывные первые производные.
Необходимым условием существования
экстремума является наличие стационарной
точки ЦФ. Т.о., основная идея многих
методов оптимизации без ограничений
в пространстве Rn
заключается в отыскании стационарной
точки x*,
в которой градиент ЦФ
Градиентные
методы работают следующим образом.
Исходя из начальной точки x0,
вычисляют
В
этом семействе методов следует выделить
методы градиента с заданным шагом, в
которых заранее задаются значения Доказано,
что построенная последовательность
сходится к решению, т.е.
1)
2)
Данная процедура ("метод расходящегося ряда") может оказаться медленной. Критерии останова (наиболее употребительные). Пусть
1)
Необходимо учитывать точность ПЭВМ. Метод наискорейшего спуска (метод Коши) В
этом широко используемом методе (МК)
Алгоритм Коши. Ш.
1 Выбрать начальную точку
Ш.
2 На
Положить
Ш. 3 Проверка критерия останова. Да:
окончание поиска Определение.
Будем говорить, что алгоритм А
глобально сходится,
если для любой выбранной исходной
точки
МК
обладает устойчивостью, т.е. при
достаточно малом значении МК
позволяет существенно уменьшить
значение ЦФ (быстро спуститься на "дно
оврага") при движении из точек,
расположенных на значительных
расстояниях от точки
Недостаток:
для некоторых типов функций сходимость
может оказаться медленной. В самом
деле, если
|
16. MO - Варианты градиентных методов на примере одного из методов: Марквардта, Флетчера-Ривза, Поллака-Рибьера. Метод Флетчера-Ривза Флетчер и Ривз расширили метод сопряженных градиентов (МГС) для квадратичных функций на случай произвольных функций. В применении к квадратичным функциям он становится равносильным методу сопряженных градиентов. К достоинствам данного метода можно отнести: малый объем памяти (необходимо хранить 3 n-мерных вектора); скорость сходимости значительно выше классических градиентных методов. Данный метод полезен для решения задач большой размерности. Алгоритм Флетчера-Ривза:
Шаг
1. Задаем начальную точку x0
положить
Шаг 2. Выбрать значение λk, минимизирующее значение функции g(λ)=f(xk+λdk)
Положить:
xk+1=xk+
λkdk
,
Шаг 3. Проверка критерия останова:
Да:
Таким
образом, на каждом этапе требуется
хранить в памяти лишь три n-мерных
вектора:
|
|
17. MO - Сравнение многомерных методов оптимизации. Сравнение методов безусловной оптимизации
Предполагается,
что выполняются следующие условия:
f(x)
дважды дифференцируема; гессиан
Для
ускоренного метода второго порядка
имеем
λm2
- второе
наибольшее собственное значение
При p=n (размерность производства) имеем суперлинейную сходимость. Но при этом на каждой итерации требуется применение (n+1) одномерных минимизаций. В таком случае метод становится эквивалентным методу сопряженного градиента. Метод Ньютона. Обладает квадратичной локальной сходимостью. На практике глобальная сходимость не гарантируется.
Методы
сопряженных направлений (относительно
метода Флетчера-Ривза).
Доказано, что
Если
К
Преимущества квазиньют-ких мет. по сравнению с методами сопряженных градиентов: требуют в n раз меньше этапов (шагов), т.е. в n раз меньше числа одномерных минимизаций. Сходимость для одного и того же поведения - квадратичная или суперлинейная. Недостатки. загрузка памяти пропорциональна n2; объем вычислений пропорционален n2. Выводы: метод Коши+дихотомия – обеспечивает нахождение наиболее точного значения ЦФ, но требует больших затрат машинного времени; метод Б-Ф-Г-Ш с использованием кубичной аппроксимации – самый эффективный по количеству вычислений функции.
|
18. MO - Формы записи задач линейного программирования (ЗЛП). Графическое решение ЗЛП с 2-мя переменными. Общий вид задачи линейного программирования записывается следующим образом:
найти минимум
(максимум)
Задачу линейного программирования (5.1 – 5.3), например, можно записать таким образом:
при ограничениях:
Здесь: n
– число переменных; m
– число ограничений; A={aij}
- действительная
матрица ограничений размерностью
(m×n);
aij
- коэффициенты при переменных в
ограничениях (5.2), (5.5); C=(c1,c2,…,cn)
– вектор–строка,
cj
– коэффициенты при переменных в
целевой функции (5.1), (5.4); b=(b1,b2,…,bm)T
– вектор
правой части ограничений;
Стандартная форма задач линейного программирования (в матричной записи). Задача линейного программирования имеет стандартную (каноническую) форму, если все ее ограничения имеют форму равенства (кроме ограничений не отрицательности переменных xj≥0): min f(x)=Cx; Ax=b; x≥0. Задачи линейного программирования со смешанными ограничениями. min f(x)=Cx; A1x=b1; A2x=b2; x≥0. Замечание: Если ищется максимум целевой функции f(x), то заменой целевой функции на -f(x) сводят исходную задачу к минимизации функции min[-f(x)]. Основные методы решения задач линейного программирования ориентированы на использование стандартной формы записи. Любую задачу линейного программирования можно представить в стандартной форме, введя дополнительные переменные. Графическое решение задач линейного программирования с двумя переменными Пример: Задача технического контроля: min f=40x1+36x2,5x1+3x2≥45;x1≥0; x2≥0. В качестве первого шага решения следует определить все возможные неотрицательные значения x1, x2, которые удовлетворяют ограничениям. Например, для точки x=(8;10) выполняются все ограничения. Такая точка называется допустимым решением. Множество всех допустимых точек называется допустимой областью или ОДР. Решение задачи линейного программирования состоит в отыскании наилучшего решения в ОДР. Для изображения ОДР следует начертить графики всех ограничений. Все допустимые решения лежат в первом квадранте, так как x1, x2≥0. В силу ограничения 5x1+3x2≥45 все допустимые решения (x1, x2) располагаются по одну сторону от прямой 5x1+3x2=45. Нужную полуплоскость можно найти, проверив, например, удовлетворяет ли начало координат неравенству (5.12). Нужная полуплоскость отмечается штриховкой. Аналогичным образом представлены ограничения x1≤8, x2≤10. ОДР или многогранник (n>2) решений MABC содержит бесконечное число допустимых точек с минимальным значением целевой функции f(x). Если зафиксировать значение целевой функции f=40x1+36x2, то соответствующие ему точки будут лежать на некоторой прямой. При изменении величины f прямая подвергается параллельному переносу. Рассмотрим прямые, соответствующие различным значениям f, имеющие с ОДР хотя бы одну общую точку. Положим, f0=600. При приближении прямой к началу координат значение f уменьшается. Ясно, что для прямой, проходящей через угловую точку A=(8;1,6), дальнейшее движение невозможно. Следовательно, x*=(8;1,6) - оптимальное решение (план) и f*=(8;1,6)=377,6 – оптимальное значение целевой функции.
|
|
19. Приближенные методы решения ЗЛП на примере транспортной задачи. Содержательная постановка транспортной задачи (ТЗ) заключается в следующем: составить план перевозок однородного груза из нескольких исходных пунктов (заводов) в исходные пункты назначения (потребления) таким образом, чтобы общая стоимость перевозок была наиболее экономичной (минимальной). Цель построения модели состоит в определении количества продукции, которое следует перевезти из каждого исходного пункта в пункт назначения. Основное предположение – величина транспортных расходов на каждом маршруте прямо пропорциональна объему перевозимой продукции.
Исходная
информация:
Рассмотрим приближенный метод Фогеля для решения транспортной задачи. Этот метод является эвристическим и часто дает оптимальное и субоптимальное решение. Схема ПМФ:
Строки и столбцы с нулевыми значениями объема производства и спроса не должны использоваться при вычислении штрафов. |
20. Методы штрафных и барьерных функций. Основные виды штрафов. Их общий принцип заключается в замене исходной задачи на решение последовательности экстремальных задач без ограничений. Понятие штрафных функций Штрафная
функция (ШФ) определяется выражением:
Выражение для штрафа H определяется таким образом, чтобы допустимые точки задачи имели преимущество перед недопустимыми в отношении безусловной минимизации ШФ. Методы
внутренней точки связаны с такими H,
при которых стационарные точки функции
Методы ШФ представляют большой интерес лишь при выполнении следующих требований: 1) решения подзадач должны стремиться к решению задачи нелинейного программирования вида:
2)
сложность минимизации
3)
правило пересчета
Рассмотрим широко используемые типы штрафов и различные процедуры учета ограничений при переходе к задачам безусловной минимизации. Квадратичный
штраф
используется для учета ограничений–равенств
вида:
. При
минимизации этот штраф препятствует
отклонению величины
Здесь предпочтительнее стратегия многоэтапного последовательного приближения к решению: 1)
процесс начинают с относительно малого
R,
например, R=0,01
и находят точку минимума функции
2)
увеличивают
3)
R
увеличивают до тех пор, пока не окажется,
что элементы итерационных
последовательностей
Рассмотрим несколько типов штрафов для ограничений–неравенств. Бесконечный барьер
Для
этого штрафа функция
Так
как машинная реализация бесконечных
штрафов невозможна, то в качестве
штрафа используется большое положительное
число, например,
Логарифмический штраф.
Штраф
положителен при всех x
таких, что
Логарифмический
штраф – это барьерная функция, не
определенная в недопустимых точках
(т. е. для таких
Штраф типа обратной функции.
Очевидна
необходимость предотвращения появления
недопустимых точек, в которых
Штраф типа квадрата срезки.
H-
внешний штраф, и стационарные точки
функции
Достоинства:
функция
Штраф – обратная функция (барьерная функция) Имеем
Методы ШФ демонстрируют, с одной стороны, принципиальную возможность использования методов ШФ, а с другой стороны – их общие недостатки, а именно: сходимость метода связана с ярко выраженной нелинейностью ("овражностью") ШФ, и здесь традиционные методы безусловной минимизации могут оказаться неэффективными.
|

 т.е.
и целевая функция, и ограничения
являются линейными функциями переменных
т.е.
и целевая функция, и ограничения
являются линейными функциями переменных

 .
. Обозначим L(x,
λ) функцию Лагранжа
Обозначим L(x,
λ) функцию Лагранжа .
.  ; 7)
; 7)



 ;
5)
;
5)

 ,
где λmax,
λmin
- соответственно наибольшее и наименьшее
собственные значения матрицы Гессе
,
где λmax,
λmin
- соответственно наибольшее и наименьшее
собственные значения матрицы Гессе
 ,
,
 ;
(5.2)
;
(5.2)
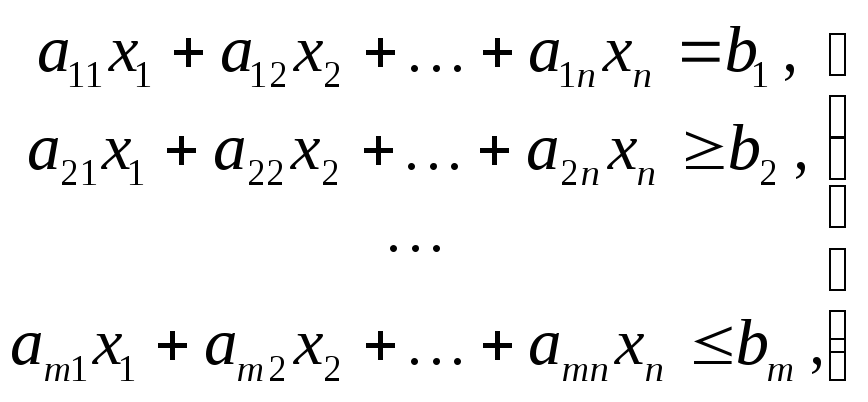 (5.5)
(5.5)

