
gos_янв_2009 / 2.1. ОТУ
.doc|
1. Сравнительный анализ временных и частотных характеристик линейных систем. Связь частотной характеристики стационарной линейной системы с весовой функцией и наоборот.
Временные
характеристики это реакция системы
на типовые функции времени. Из типовых
функций времени наиболее часто
используются две: единичная импульсная
функция и единичная ступенчатая
функция. Единичной импульсной функцией
(дельта-функцией,
Весовая или
импульсная переходная функция линейной
системы представляет собой реакцию
этой системы в момент времени
Переходный процесс
изменения во времени выходной величины
звена, обусловленной подачей на вход
этого звена единичного ступенчатого
воздействия, называется переходной
характеристикой звена
Аналогично,
фазово-частотная характеристика
показывает как измениться фаза. Между
временными и частотными характеристиками
системы есть много общего: за
характеристику системы принимается
некоторая функция двух переменных
(текущего времени и какого-либо
параметра). В импульсной характеристике
в качестве такого параметра принимается
момент действия единичного импульса,
а в частотной – круговая частота
гармонического колебания
Для физически
возможной линейной системы:
|
2. Основные задачи синтеза оптимальных систем автоматического управления (САУ) и их особенности. Классификация оптимальных САУ. Оптимальными САУ называются САУ, наилучшие в том или ином смысле. Эти системы могут быть как с обратными связями, так и без них. Синтез оптимальных САУ включает в себя следующие задачи: определение математической модели ОУ, т.е. определение функциональной зависимости выходной величины у от входного воздействия на объект uf, которая может быть задана различными способами, и в частности системой дифференциальных уравнений; оценку ограничений, как внутренних, присущих физическим процессам в ОУ, так и внешних, наложенных искусственно; определение желаемого поведения ОУ; задание определенной цели управления и выбор в соответствии с этой целью критерия оптимальности, характеризующего эффективность управления; определение стратегии УУ, т.е. такого алгоритма его работы, который при указанных выше условиях обеспечивает экстремум критерия оптимальности, т.е. максимальную эффективность управления; схемную реализацию УУ в соответствии с найденным алгоритмом его работы. Синтез оптимальных САУ имеет ряд особенностей по сравнению с синтезом других систем: 1. его цель создание САУ, в которых используются все их возможности для достижения экстремальных значений наиболее важных показателей качества управления при удовлетворении заданных требований к остальным показателям. 2. при синтезе оптимальных САУ энергетические, механические и другие ограничения учитываются как факторы, определяющие возможности САУ по реализации экстремальных значений заданных показателей качества управления. Задачи синтеза оптимальных систем делятся на два класса: 1. оптимизация программы управления, или определение оптимального управления u(t) как функции времени, переводящего ОУ из начального состояния в заданное и реализующего минимум критерия качества, т.е. определение алгоритма УУ системы; 2. определение закона управления как функции фазовых координат ОУ u(y), обеспечивающего движение ОУ по фазовой траектории, на которой реализуется минимум критерия оптимальности, т.е. определение алгоритма УУ замкнутой системы. Первый класс задач чаще всего используется как первый этап решения задач второго класса. В настоящее время существует несколько направлений классификации оптимальных систем. 1) При классификации по оптимизируемым показателям качества САУ различают следующие типы систем: оптимальные по быстродействию; оптимальные по расходу ресурсов; с минимальной энергией управления; с минимальными потерями управления. Оптимальными по быстродействию называют системы, УУ которых формирует такое допустимое управление u(t), которое переводит в фазовом пространстве изображающую точку ОУ из одного заданного состояния y(t0) в другое y(T) за минимальное время T-t0. Системы, оптимальные по расходу ресурсов, переводят в фазовом пространстве изображающую точку ОУ из начального состояния в заданную область V с минимальными затратами ресурсов (топлива, катализатора и т.п.).
Системами
с
минимальной энергией управления
называют системы, которые при переводе
изображающей точки ОУ из начального
положения в заданное обеспечивают
минимум функционала
Системы с минимальными потерями управления, переводя изображающую точку ОУ из начального состояния в заданное, минимизируют отклонение действительных координат объекта от предписанных значений. 2) Вторым направлением классификации оптимальных систем является классификация по характеристикам ОУ. Системы делятся на непрерывные, дискретно-непрерывные и дискретные. В непрерывных системах координаты ОУ и воздействия на него не квантованы ни по времени, ни по уровню. В дискретно-непрерывных системах эти величины квантованы по времени, а в дискретных и по времени, и по уровню. Различают оптимальные системы и по типам дифференциальных уравнений ОУ и делят их на системы с линейными, нелинейными объектами и объектами с распределенными параметрами, динамика которых описывается дифференциальными уравнениями в частных производных. Важными характеристиками ОУ являются ограничения, накладываемые на управление u(t), на его координаты и на возмущения, действующие на него. Поэтому при определении классов оптимальных систем различают: системы с ограничением на управление, когда в системе должны выполняться неравенства
системы с ограничениями на координаты ОУ и с ограничениями на возмущения; ограничения на координаты и возмущения могут накладываться как в виде неравенств (9.2), так и в виде ограничений на функционалы координат и возмущений. 3) Третьим направлением классификации оптимальных систем является классификация по характеру критерия оптимальности. При этом различают следующие типы систем: равномерно - оптимальные; статистически - оптимальные; минимаксно - оптимальные. К первому типу относятся такие системы, процессы в которых в каждом отдельном случае являются оптимальными. Например, равномерно-оптимальная по расходу топлива система ориентации космического корабля будет переводить его из любого произвольного положения в заданное с минимальным расходом топлива. Системы второго типа оптимальны не в каждом отдельном случае, а в среднем, т.е. они дадут наилучший средний результат по сравнению с неоптимальными системами при большом количестве опытов. К ним относятся системы, на процессы в которых так или иначе влияют случайные факторы. Минимаксно-оптимальные системы обеспечивают наилучший по сравнению с неоптимальными САУ результат только в наихудшем случае, т.е. наихудший результат в такой системе лучше, чем наихудший результат в неоптимальной системе. В зависимости от полноты и характера информации, поступающей на УУ, оптимальные системы делятся на три типа: 1) оптимальные системы с полной или максимально возможной информацией об ОУ; 2) оптимальные системы с неполной информацией об ОУ и независимым (пассивным) ее накоплением в процессе управления; 3) оптимальные системы с неполной информацией об ОУ и активным ее накоплением в процессе управления. К системам третьего типа относятся системы со структурной схемой.
|
||||||||||||||||||||||||
|
3. Понятие о законе управления. Принципы Ползунова-Уатта и Понселе.
Под
законом
регулирования или, в более общем
случае, законом управления
понимается математическая форма
преобразований задающих воздействий,
возмущений, воздействий обратных
связей, определяющих управляющие
воздействия u(t).
Т.е. это функциональная зависимость,
в соответствии с которой УУ формирует
управляющие воздействия u(t).
Она может быть представлена в следующем
виде:
Опишем
линейные законы, когда УУ (регулятор)
вырабатывает величину u(t)
в функции ошибки в соответствии с
линейной формой:
При
рассмотрении этих линейных законов
дополнительно предположим, что ОУ
(ОР) представляет собой звено статического
типа. Это означает, что в установившемся
состоянии между регулируемой величиной
и управляющим воздействием существует
пропорциональная зависимость при
равенстве нулю возмущающих воздействий:
|
4. Импульсные САУ. Виды модуляции. Особенности цифровых САУ. Кодоимпульсная модуляция. В соответствии с тремя способами квантования дискретные системы делят на три основных типа: импульсные, релейные и релейно-импульсные, или цифровые, САУ. Чаще всего под дискретными системами понимают только системы, в которых осуществляется квантование по времени, т.е. импульсные и цифровые. Импульсные САУ характеризуются наличием импульсного элемента, выходная величина которого представляет собой последовательность импульсов. Один из параметров импульса (амплитуда, длительность, момент начала действия импульса) является функцией входной величины. Различают три вида модуляции импульсов:
1)
амплитудно-импульсную модуляцию
(АИМ), при которой амплитуда импульсов
a
зависит от значения входного сигнала
в момент начала действия импульса tn,
т.е.
2)
широтно-импульсную модуляцию (ШИМ),
при которой длительность импульса Tn
зависит от значения входного сигнала
в момент начала действия импульса,
т.е.
3)
временную импульсную модуляцию (ВИМ),
при которой временной сдвиг Tc
(запаздывание) импульса зависит от
значения входного сигнала в определенный
момент времени, т.е.
Особенности цифровых САУ. Непрерывный выходной сигнал y(t) объекта управления преобразуется в цифровую форму АЦП. Преобразование осуществляется в моменты квантования tn и заключается в квантовании непрерывной величины по времени, по уровню и представлении полученных дискретных значений в виде чисел, т.е. в цифровом коде. В зависимости от принципа действия АЦП это преобразование может осуществляться либо путем последовательного выполнения перечисленных выше действий, либо сразу в виде одной операции. Описываемое преобразование называется кодоимпульсной модуляцией. Поэтому цифровые системы иногда именуют кодо-импульсными системами. Соответственно АЦ-преобразование называют кодированием, а обратное ЦА-преобразование декодированием.
|
||||||||||||||||||||||||
|
5. Основные линейные законы регулирования: краткая характеристика законов и их сравнительный анализ. Под законом регулирования или, в более общем случае, законом управления понимается математическая форма преобразований задающих воздействий, возмущений, воздействий обратных связей, определяющих управляющие воздействия u(t). Иными словами, это функциональная зависимость, в соответствии с которой УУ формирует управляющие воздействия u(t). Она может быть представлена в следующем виде: u(t)=F(x,g,f), где F некоторая, в общем случае нелинейная, функция от ошибки x, задающего воздействия g и возмущающего воздействия f, а также от их производных и интегралов по времени.
1)
Пропорциональное регулирование Для
простейшего безынерционного УУ закон
пропорционального регулирования
имеет следующий вид:
Передаточная
функция
Однако
существенным здесь является то
обстоятельство, что цепь регулирования
представляет собой статическое
(позиционное) звено и при
Передаточная
функция разомкнутой системы равна:
В
установившемся состоянии передаточная
функция стремится к величине
Для
установившегося состояния замкнутой
системы при постоянном задающем
воздействии
Ошибка (рассогласование) системы x(t) обусловлена как погрешностями реальной аппаратуры, так и самим принципом построения УУ (регулятора). При этом меняющаяся в процессе регулирования так называемая динамическая ошибка x(t) в установившемся режиме может перейти в некоторое постоянное отклонение регулируемой величины от g0=const, называемое статической ошибкой xуст. Из приведенной выше формулы следует, что пропорциональное регулирование позволяет уменьшить установившиеся ошибки в объекте в (1+К) раз. Регулирование получается статическим, так как при любом конечном значении коэффициента усиления цепи установившаяся ошибка будет отличной от нуля.
2.
Интегральное регулирование При
интегральном регулировании осуществляется
пропорциональная зависимость между
скоростью изменения регулирующего
воздействия и ошибкой, т.е.
Иными
словами, регулирующее воздействие
получается пропорциональным интегралу
от ошибки по времени
Передаточная
функция разомкнутой САР имеет следующий
вид:
При
интегральном регулировании получается
система, астатическая по отношению к
задающему воздействию (астатизм
первого порядка). Она может быть при
этом как статической, так и астатической
по отношению к возмущающим воздействиям
(в астатической системе
Передаточная функция разомкнутой системы для интегрального регулирования может быть представлена в виде
В
физическом смысле
Регулирование
может осуществляться и по двойному
интегралу от ошибки по времени
Передаточная
функция разомкнутой системы при таком
регулировании равна
где
Для
установившегося значения имеем
Система также будет обладать астатизмом относительно задающего воздействия. Однако это будет уже астатизм второго порядка.
Ошибка,
определяемая задающим воздействием,
будет равна нулю не только при g=const,
но и при изменении задающего воздействия
с постоянной скоростью
Аналогичным
образом можно получить астатизм
третьего и выше порядков, вводя
регулирование по третьему и высшим
интегралам, т.е. осуществляя регулирование
по закону
3.
Изодромное регулирование
При изодромном законе регулирования
осуществляется регулирование
одновременно по пропорциональному и
интегральному законам, т.е.
Здесь
Изодромное регулирование может осуществляться при помощи изодромных звеньев. Изодромное регулирование сочетает в себе высокую точность интегрального регулирования (астатизм) с большим быстродействием пропорционального регулирования. В первые моменты времени при появлении ошибки система изодромного регулирования работает как система пропорционального регулирования. Это определяется первым слагаемым. В дальнейшем система начинает работать как система интегрального регулирования, так как с течением времени преобладающее значение начинает приобретать второе слагаемое в законе.
4.
Регулирование по производным При
регулировании по первой производной
от ошибки реализуется следующая
зависимость:
Регулирование по производной не имеет самостоятельного значения, т.к. в установившемся состоянии производная от ошибки равна нулю и регулирование прекращается. Однако оно может играть весьма большую роль в переходных процессах и вообще в динамике в качестве вспомогательного средства, так как такое регулирование позволяет учитывать не только наличие ошибки, но и тенденцию к ее росту или уменьшению.
При
осуществлении регулирования по закону
В результате введение регулирования по производной от ошибки увеличивает скорость реакции САР, повышает ее быстродействие, что приводит к снижению ошибок в динамике.
|
6. Весовая (импульсная переходная) функция дискретной линейной системы. Весовые коэффициенты дискретных линейных систем. Особенности описания стационарных дискретных линейных систем.
Пусть
реакция дискретной линейной системы
на кратковременное возмущение, равное
единице и действующее только в течение
времени действия k-импульса.
Тогда ее реакция на кратковременное
возмущение, равное x(tk)
и действующее только в течение времени
действия k-го
импульса, будет на основании принципа
суперпозиции равна
Реакция
дискретной линейной системы на всю
последовательность импульсов,
модулированных входным возмущением
x(t),
в силу принципа суперпозиции определится
формулой
Это основная формула, определяющая зависимость выходной переменной дискретной нестационарной линейной САУ от входного сигнала.
Функции
Весовые
коэффициенты
Для физически возможной дискретной линейной системы, находящейся в покое до момента t0, формула примет следующий вид:
Если
положить в
Следовательно,
весовая функция любой дискретной
линейной системы представляет собой
линейную комбинацию
Дискретную
систему назовем стационарной, если
при сдвиге во времени входного
возмущения без изменения его формы
на интервал времени, кратный периоду
повторения импульсов, выходная
переменная сдвигается во времени на
такой же интервал без изменения своей
формы, т.е. дискретная система может
быть стационарной только тогда, когда
действующие на систему входные
возмущения следуют друг за другом
через равные промежутки времени. По
определению, весовой коэффициент
Если
система стационарна, то при сдвиге
кратковременного единичного возмущения
во времени на интервал
Для стационарной
дискретной линейной системы весовые
коэффициенты
Обозначая
разность индексов m,
т.е. l-i=m,
введем для весовых коэффициентов
обозначение
Весовые
коэффициенты последовательного
соединения ИЭ и непрерывной стационарной
линейной системы определяются формулой
Для
стационарной дискретной линейной
системы принимает вид
|
||||||||||||||||||||||||
|
7. Алгебраические критерии устойчивости САУ. Достоинства и недостатки этих критериев. Понятие устойчивости САУ связано с ее способностью возвращаться в состояние равновесия (устойчивый режим работы) после исчезновения внешних сил, которые вывели САУ из этого состояния. Устойчивость это свойство системы возвращаться в заданный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия. Линейная система называется устойчивой, если ее выходная переменная остается ограниченной при любых ограниченных по абсолютной величине входных возмущениях. Известно несколько критериев устойчивости в аналитической (алгебраической) форме: Рауса, Гурвица, Шур-Кона, Льенара-Шипара, Джури-Бланшара, различающихся не по сути, а по форме, поэтому, например, первые два часто называют критерием Рауса-Гурвица. Эти критерии сводят условия устойчивости к выполнению ряда алгебраических неравенств, связывающих коэффициенты уравнения системы. Посредством алгебраических критериев определяются условия устойчивости САУ при n≤15.
Критерий
Рауса-Гурвица.
Отметим, что критерий Гурвица достаточно
просто можно получить из критерия
Рауса. Критерий Рауса формулируется
в табличной форме. Таблица Рауса
состоит из коэффициентов
В
таблице Рауса строка
Критерий
устойчивости Рауса.
САУ устойчива, если коэффициенты
первого столбца таблицы при
В
критерии
устойчивости Гурвица
также рассматривается полином
Он
называется определителем Гурвица и
имеет размерность (n
x
n).
Первая строка определителя содержит
все нечетные коэффициенты, начиная с
Критерий
устойчивости Гурвица
заключается в требовании положительности
определителя Гурвица и всех его
диагональных миноров при
Недостатки критерия устойчивости Рауса-Гурвица: 1) условия устойчивости усложняются с ростом порядка системы;
2)
для системы достаточно высокого
порядка (
Критерий
Льенара-Шипара.
При
|
8. Метод точечных преобразований (отображений) в теории автоматического управления. Для пояснения идеи метода точечных преобразований предположим, что изображающая точка в какой-то момент времени занимает положение X с координатой x на положительной полуоси 0x1. После обхода вокруг начала координат изображающая точка пересечет полуось 0x1 в некоторой точке Y, имеющей координату y. Через каждую точку полуоси 0x1 можно провести одну и только одну фазовую траекторию, поэтому обходу изображающей точки вокруг начала координат соответствует переход каждой точки полуоси 0x1 в некоторую другую точку той же полуоси. Другими словами, обходу изображающей точки вокруг начала координат (либо другой особой точки на фазовой плоскости) соответствует точечное преобразование любой полуоси (в общем случае полупрямой), выходящей из начала координат, в саму себя. Если при этом преобразовании какая-нибудь точка полуоси (полупрямой) переходит в саму себя, т.е. остается неподвижной, то через эту точку проходит замкнутая фазовая траектория предельный цикл. Таким образом, для нахождения предельных циклов и определения параметров соответствующих автоколебаний достаточно найти неподвижные точки точечного преобразования какой-либо полупрямой, выходящей из соответствующей особой точки фазовой плоскости. Каждой точке выбранной полупрямой соответствует некоторое положительное число, равное расстоянию этой точки от начала координат (или от соответствующей особой точки). Поэтому точечное преобразование выбранной полупрямой при обходе изображающей точки вокруг начала координат (особой точки) определяет однозначную возрастающую функцию y=f(x), которая может быть изображена кривой в координатах 0xy. Определение y по x (т.е. нахождение точки Y по точке X) называется точечным преобразованием. Зависимость y=f(x) описывает точечное преобразование положительной полуоси 0x1 в саму себя, происходящее при обходе изображающей точки начала координат. Каждая точка этой кривой с одинаковыми абсциссой и ординатой, т.е. точка пересечения ее с биссектрисой координатного угла y=x является неподвижной точкой преобразования, определяет предельный цикл и амплитуду возможных автоколебаний в системе. Участкам кривой y=f(x), лежащим ниже биссектрисы координатного угла y=x, соответствуют спиральные фазовые траектории, по которым изображающая точка приближается к началу координат, т.е. колебательный процесс является затухающим. Участкам кривой y=f(x), лежащим выше биссектрисы координатного угла y=x, соответствуют спиральные фазовые траектории, по которым изображающая точка удаляется от начала координат, следовательно, колебательный процесс является расходящимся. Таким образом, вид функции y=f(x) и взаимное расположение кривой точечного преобразования y=f(x) и биссектрисы координатного угла y=x позволяют судить о характере поведения нелинейной системы около положения равновесия. При этом, если кривая y=f(x) пересекает биссектрису y=x сверху вниз, то автоколебания устойчивы, а если снизу вверх неустойчивы. Метод точечных преобразований позволяет исследовать характер возможных режимов в системе, не строя фазового портрета. Метод удобен, в частности, для определения влияния изменения разных параметров системы на характер переходных процессов в ней. При этом могут быть определены критические, так называемые бифуркационные значения параметров, переход через которые качественно меняет фазовый портрет системы. Существует 55-летняя традиция успешного применения метода точечных преобразований для исследования кусочно-линейных систем невысокого порядка.
|
||||||||||||||||||||||||
|
9. ОТУ - Второй (прямой) метод Ляпунова. Второй метод Ляпунова связан с физическими представлениями о равновесии материальной точки в консервативном силовом поле. Основная идея состоит в нахождении такой функции координат точки пространства состояний системы V(η1,…, ηn), которая была бы до некоторой степени аналогична потенциальной энергии покоящейся материальной точки в обычном пространстве. Функция V(η1,…, ηn) называется знакопостоянной, если она имеет один и тот же знак всюду в некоторой области, содержащей начало координат, за исключением некоторых точек, в которых она равна нулю. Знакопостоянная функция, равная нулю лишь в начале координат, называется знакоопределенной : определенно-положительной или определенно - отрицательной, в зависимости от знака. Например, в трехмерном пространстве (n=3) функция
А.М. Ляпунов доказал следующие две теоремы. Теорема 1. Если дифференциальные уравнения возмущенного движения таковы, что можно найти знакоопределенную функцию V, полная производная которой по времени
в силу этих уравнений знакопостоянна и имеет знак, противоположный знаку функции V, или тождественно равна нулю, то невозмущенное движение устойчиво. Теорема 2. Если дифференциальные уравнения возмущенного движения таковы, что можно найти знакоопределенную функцию V, полная производная которой по времени в силу этих уравнений знакоопределенна и имеет знак, противоположный знаку функции V, то невозмущенное движение асимптотически устойчиво. Функции V, удовлетворяющие условиям теорем 1, 2, называются функциями Ляпунова. Второй (прямой) метод оценки устойчивости дает достаточные условия устойчивости, т.е. движение системы может быть устойчивым и при невыполнении условий теорем 1, 2 Ляпунова. Метод исследования устойчивости с помощью функции Ляпунова V(η1,…, ηn) эффективен и применим к любым нелинейным системам, так как он не накладывает каких-либо ограничений на правые части уравнений движения системы. Однако практическое применение этого метода осложнено трудностью нахождения функции Ляпунова V(η1,…, ηn). |
10. Первый метод Ляпунова. Первый метод Ляпунова основан на линеаризации уравнений, описывающих поведение системы.
Линеаризация
осуществляется разложением всех
входящих в уравнение функций
Получим
систему линейных дифференциальных
уравнений относительно
Величины
Теоремы А.М.
Ляпунова, справедливые для автономных
систем, для которых
Первый метод Ляпунова основан на линеаризации уравнений, описывающих поведение системы. Теорема 1. Если вещественные части всех корней характеристического уравнения первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво независимо от членов разложения выше первого порядка малости. Теорема 2. Если среди корней характеристического уравнения первого приближения найдется по меньшей мере один с положительной вещественной частью, то невозмущенное движение неустойчиво независимо от членов разложения выше первого порядка малости. Данные теоремы позволяют однозначно разрешить вопрос об устойчивости (или неустойчивости) невозмущенного движения автономной нелинейной системы на основании исследования уравнений первого приближения только для структуры корней характеристического уравнения, указанной в условиях теорем. Если структура корней характеристического уравнения другая, то для определения характера устойчивости одних уравнений первого приближения недостаточно и необходимо рассмотреть влияние членов второго и высшего порядка малости.
В
общем случае, когда коэффициенты
Выполнив
эти вычисления для различных моментов
времени t,
можно судить об устойчивости системы.
Если интегралы для весовых (импульсных
переходных) функций, соответствующих
всем входам системы и всем переменным
Изложенный метод исследования устойчивости нелинейных систем, основанный на линеаризации уравнений, описывающих поведение системы, применим лишь к системам, содержащим только элементарные нелинейные звенья с непрерывными гладкими характеристиками. К системам с существенными нелинейностями этот метод не применим. В таких случаях оказывается полезным второй метод Ляпунова.
|
||||||||||||||||||||||||
|
11. Синтез оптимальных дискретных САУ методом динамического программирования.
В
Принцип
оптимальности означает, что если
траектория
Этот
принцип оптимальности не является
всеобщим. Он
справедлив
для систем, у которых оптимальная
траектория не зависит от предыстории
системы, а целиком определяется
исходным ее состоянием.
В данном случае справедливость принципа
оптимальности очевидна: если траектория
Сформулированный принцип оптимальности является весьма общим необходимым условием оптимального процесса, справедливым как для непрерывных, так и для дискретных систем. В основу этого метода положен следующий принцип оптимальности: любой конечный участок оптимальной траектории является тоже оптимальной траекторией, т.е. часть оптимальной траектории от любой промежуточной точки до ее конца является оптимальной траекторией между этими точками, если считать данную промежуточную точку началом траектории. Метод динамического программирования для непрерывных систем на примере синтеза оптимального управления ОУ с ограниченными координатами. Требуется перевести изображающую точку ОУ в пространстве состояний из состояния y(0) в некоторую область пространства состояний (фазового пространства) за определенное время T, минимизируя функционал
Условия, которым должны удовлетворять фазовые координаты объекта и управляющие воздействия на него, в векторной форме могут быть записаны в виде:
где V область фазового пространства, из которой не должна выходить экстремаль y(t); M замкнутое ограниченное множество функций, из которого выбираются кусочно-непрерывные управления u(t); y, F – n-мерные векторы; u, F0 скалярные функции. Если за начало отсчета взять не t=0, а некоторую другую точку t1 интервала [0,T], а в качестве начальных условий выбрать новую точку y(t1) из области V и найти оптимальное управление, минимизирующее функционал
Если
эта функция определена при t=0,
Если
функция
при
условиях (9.52) и
Существование непрерывно дифференцируемой функции S(t, y) решения уравнения (9.63) является достаточным условием оптимальности. Если существует решение уравнения (9.63), то соответствующее ему управление u(t, y) будет реализовывать минимум критерия оптимальности (9.50). Достоинства метода динамического программирования: оптимальное управление определяется как функция фазовых координат ОУ, что упрощает синтез замкнутых оптимальных САУ; он применим для синтеза как равномерно-оптимальных, так и статистически-оптимальных систем; принципу оптимальности Беллмана удовлетворяют только те оптимизирующие функции S(t, y), которые одновременно являются функциями Ляпунова для замкнутой системы. Следовательно, соответствующие этим функциям управления u(t, y) и формирующие их УУ не только обеспечивают минимум критерия качества, но и устойчивость замкнутых систем; позволяет получать физически понятные алгоритмы решения задач оптимального управления на ЭВМ.
|
12. Структура интеллектуальной СУ. ИСУ с экспертной системой (регулятором). Понятие «интеллектуальная система» возникло лет тридцать тому назад. С течением времени развитие этого нового научного направления, получившего в дальнейшем название «искусственный интеллект», особенно таких его разделов, как инженерия знаний, компьютерные логика и лингвистика, когнитивная психология, методы поиска и принятия решений, модели обучения, подготовило теоретическую основу для создания программных систем по обработке и использованию знаний для успешного решения многих прикладных задач, включая создание систем, моделирующих творческие возможности человека. Такие системы стали называть «интеллектуальными», а применительно к области управления получил распространение термин «интеллектуальные системы управления». В структуре любой ИСУ содержатся следующие основные блоки: база знаний с развитыми механизмами вывода на знаниях, интеллектуальный решатель (формулирующий постановку и общий план решения задачи), интеллектуальный планировщик (формирующий конкретный план решения задачи), система объяснения и интерфейс с пользователем. Иерархическая структура ИСУ соответствует базовому принципу, который считается в теории интеллектуальных систем фундаментальным. Принцип имеет аббревиатуру IPDI (Increasing Precision with Decreasing Itelligence) и означает, что по мере продвижения к высшим уровням иерархической структуры ИСУ повышается интеллектуальность системы, но снижается ее точность, и наоборот. Для ИСУ справедливы следующие пять принципов: информационное взаимодействие ИСУ с реальным внешним миром с использованием специально организованных информационных каналов связи; принципиальная открытость системы для повышения интеллектуальности и совершенствования собственного поведения; наличие механизмов прогноза изменений внешнего мира и собственного поведения системы в динамически меняющемся внешнем мире; многоуровневая иерархическая структура, построенная в соответствии с правилом: повышение интеллектуальности и снижение требований к точности по мере повышения ранга иерархии в системе (и наоборот); сохраняемость функционирования (возможно с некоторой потерей качества или эффективности, т.е. с некоторой деградацией) при разрыве связей или потере управляющих воздействий от высших уровней иерархии. ИСУ организованные и функционирующие в соответствии с пятью принципами (в полном их объеме), называются ИСУ, обладающими свойством «интеллектуальности в большом». Из определения следует, что системы, обладающие свойством «интеллектуальности в большом», должны иметь многоуровневую иерархическую структуру со следующими уровнями (в порядке понижения ранга): самоорганизации (самоперестройки по результатам обучения); обучения; прогноза событий; адаптации; формирования решений; работы с базами событий и знаний; планирования операции по реализации сформированного решения; исполнительный. ИСУ, структурно не организованные в соответствии с приведенными выше пятью принципами, но использующие при функционировании знания (например, в виде правил) как средство преодоления неопределенности входной информации, модели САУ или ее поведения, называются ИСУ, обладающими свойством «интеллектуальности в малом». В ИСУ, интеллектуальных в большом, на верхних уровнях иерархической управляющей структуры используются, как правило, экспертные системы. Структура ИСУ включает пять основных блоков. Блок «Интеллектуальный интерфейс» служит для связи с экспертом в области управления и используется в основном для обучения системы. Блок «Симулятор» осуществляет моделирование развития текущей ситуации (прогноз) и в некоторых случаях может выполнять функции анализа путей развития процессов, приведших к текущей ситуации. В настоящее время ведутся интенсивные исследования по созданию ИСУ на основе экспертных регуляторов, использующих технологию инженерии знаний и рассуждений на знаниях.
В
|
||||||||||||||||||||||||
|
13. Принципы управления и классификация САУ. Классификационные признаки, характеризующие понятия, относящиеся к принципам управления, выделим на основе анализа факторов, определяющих алгоритм или закон управления, т.е. выработку и осуществление управляющих воздействий. Признаки классификации САУ При классификации САУ по виду задающего сигнала выделяют частный, но широко распространенный тип САУ, которые называются системами автоматического регулирования (САР).
САР - это САУ, задачей которой является поддержание выходной величины ОУ у на заданном уровне g, т.е. поддержание равенства y=g. В зависимости от характера задающего воздействия САР делятся на три вида : 1. Системы автоматической стабилизации, задающий сигнал в которых g(t)=const, а выходной параметр САУ поддерживается на уровне заданного значения (y(t)=const); 2. системы программного управления, задающий сигнал в которых g(t) зависит от известной задающей программы. Это, например, числовое программное устройство управления станком; 3. следящие системы, изменение задающего сигнала в которых происходит по неизвестному закону, заданному тем или иным способом. По топологии функциональной схемы (по степени связности процессов в объекте и степени сложности структуры объекта управления) различают следующие виды САУ: 1. одноконтурные САУ с одной регулируемой величиной (системы включают в себя один канал обратной связи) - одномерные САУ; 2. многоконтурные САУ с одной регулируемой величиной (включают в себя один канал главной обратной связи и несколько каналов местной обратной связи) и многоконтурные САУ с несколькими регулируемыми величинами (содержат несколько каналов главных обратных связей и также могут быть местные обратные связи) многомерные САУ. Многомерные САУ в свою очередь подразделяются на: 1. многоконтурные несвязанные системы это такие системы, в которых УУ (регуляторы) не связаны между собой вне объекта управления; 2. многоконтурные зависимые системы это системы, в которых изменение одной величины приводит к изменению других регулируемых величин; По воздействию чувствительного (измерительного) элемента на регулирующий орган (РО) различают системы прямого и косвенного управления. В системах прямого управления непосредственно происходит передача воздействия чувствительного элемента (поплавка) на РО (задвижку). Недостаток такой системы очевиден, так как необходимо достаточно большое количество энергии для передачи воздействия ЧЭ на РО. Однако такой энергии часто не имеется. Кроме того, реакция РО на ЧЭ снижает его чувствительность и значительно уменьшает точность работы системы. Поэтому в системах, где необходима повышенная точность управления и нет достаточной энергии для прямого регулирования, применяют косвенное управление. По виду зависимости регулируемой величины от внешнего воздействия различают статические и астатические САУ: 1. статические САУ это системы, в которых при возмущающем воздействии регулируемая величина y(t) по окончании переходного процесса принимает значения, пропорциональные возмущающему воздействию. В этих системах статическое звено САУ имеет между выходной и входной величинами строго определенную функциональную связь, которую принято называть статической характеристикой y=F(x); 2. астатические САУ это системы, в которых при внешнем воздействии f и окончании переходного процесса значение регулируемой величины устанавливается равным заданному, т.е. в установившемся режиме разность между заданным и текущим значениями регулируемой величины равна нулю. По виду воздействия регулирующего органа (или ИЭ, УУ) на объект управления, т.е. по виду управляющих воздействий, различают непрерывные и дискретные системы. По характеру звеньев, включаемых в САУ, системы делятся на линейные и нелинейные.
|
14. Коррекция динамических свойств САУ: краткая характеристика корректирующих звеньев и их сравнительный анализ.
Коррекция
динамических свойств САУ используется
для выполнения требований по
устойчивости, точности и качеству
процессов управления. Коррекция
осуществляется с помощью введения в
систему специальных корректирующих
звеньев с определенной, заранее
подобранной передаточной функцией
Последнее
объясняется тем, что в замкнутом
контуре САУ КЗ, изображенное на рис.
6.1, б),
тоже может рассматриваться как обратная
связь, но относительно другой части
САУ, показанной пунктиром. С другой
стороны, схему на рис. 6.1, б)
можно свести и к последовательной
коррекции (рис. 6.1, а),
принимая за передаточную функцию КЗ
сумму
Звенья: 1. Пропорционально-дифференцирующее последовательное корректирующее звено
Изучение
пропорционально-дифференцирующих
(ПД) КЗ начнем с идеального
пропорционально-дифференцирующего
звена,
имеющего передаточную функцию вида
2. Инерционное (реальное) пропорционально-дифференцирующее звено В большинстве случаев ПД-звенья имеют существенную инерционность, и тогда их передаточная функция имеет следующий вид:
Инерционное (реальное) ПД-звено можно представить как последовательное соединение идеального ПД-звена и апериодического звена первого порядка.
3. Пропорционально-интегрирующее последовательное корректирующее звено Передаточная функция пропорционально-интегрирующего корректирующего звена (ПИ-звена) имеет вид
Формулу выше перепишем следующим образом :
Следовательно, ПИ-звено эквивалентно последовательному соединению интегрирующего звена и ПД-звена. Такое звено применяется вместо обычного интегрирующего звена для повышения порядка астатизма в тех случаях, когда введение интегрирующего звена требует дополнительной коррекции для сохранения устойчивости и необходимого качества переходных процессов. Знак воздействия по интегралу должен быть положительным, а знак воздействия по производной может быть любым. По частотным свойствам рассматриваемое звено противоположно ПД-звену и является фильтром нижних частот.
4. Пропорционально-интегродифференцирующее последовательное корректирующее звено Передаточная функция пропорционально-интегродифференцирующего последовательного корректирующего звена (ПИД-звена) имеет следующий вид:
Из этого следует, что данное звено эквивалентно последовательному соединению интегрирующего звена и ПД-звена с воздействиями по двум производным либо, что то же самое, ПИ-звену и ПД-звену с одной производной. Следовательно, рассматриваемое звено повышает порядок астатизма, но дает более сильную коррекцию динамических свойств САУ по сравнению с ПИ-звеном. Частотные характеристики ПИД-звена получаются сложением характеристик рассмотренных выше ПД- и ПИ-звеньев, поэтому такое звено подчеркивает как верхние, так и нижние частоты, подавляя средние.
5. Параллельные корректирующие звенья обратные связи
При
охвате основного звена с передаточной
функцией
В
ТАУ принято параллельные КЗ называть
корректирующими обратными связями,
поэтому в дальнейшем изложении будем
придерживаться данной традиции. Кроме
этой классификации корректирующие
обратные связи делятся на жесткие и
гибкие. Жесткая
обратная связь
представляет собой статическое звено,
т.е.
Основные виды корректирующих обратных связей:
идеальная
жесткая обратная связь
идеальная
гибкая обратная связь
Возможны и более сложные передаточные функции корректирующих обратных связей.
6. Сравнение последовательных и параллельных корректирующих звеньев
Для
линейных систем рассматриваемые типы
коррекции эквивалентны, т.е. каждая
из них дает полностью подобные в
динамическом отношении САУ.
Эквивалентность последовательной и
параллельной коррекции выводится и
из условия равенства
отрицательные обратные связи уменьшают отрицательное влияние нелинейностей, имеющихся в охваченной основной части системы, и нестабильность параметров системы, что также объясняет их основное применение в технике САУ.
|
||||||||||||||||||||||||
|
15. ОТУ - Инвариантность: основные понятия и количественные оценки инвариантности. Инвариантность управляемой (регулируемой) переменной y(t) САУ к возмущениям f(t) и ковариантность с задающим воздействием g(t) являются важнейшими требованиями к процессу управления в САУ. В теории инвариантности приняты следующие определения: САУ является инвариантной по отношению к возмущающему воздействию f(t), если после завершения переходного процесса, определяемого начальными условиями, управляемая (регулируемая) величина y(t) и ошибка x(t) системы не зависят от этого воздействия; САУ является инвариантной по отношению к задающему воздействию g(t), если после завершения переходного процесса, определяемого начальными условиями, ошибка x(t) системы не зависит от этого воздействия. Во втором определении рассматривается инвариантность ошибки САУ x(t)=g(t)-y(t) к задающему воздействию g(t), т.е. управляемая переменная y(t) должна совпадать с задающим воздействием g(t). Этот факт обозначается термином «ковариантность». Под абсолютной инвариантностью переменной x(t) понимается полная независимость вынужденных движений от воздействий ψ(t). Частичная инвариантность. Система будет инвариантна к входным воздействиям, которые могут быть представлены в виде степенной функции времени с положительными и ограниченными степенями, в виде суммы экспонент с заданными постоянными времени и т.п. Понятие инвариантности системы по отношению к какому-либо входному воздействию с точностью до ε. Иными словами, если вынужденные движения xвын(t) при ограниченных воздействиях ограничены, то говорят об инвариантности до ε. Понятие «селективная инвариантность», которое означает независимость установившейся реакции системы xвын(t) на воздействие ψ(t) ψ(t) определенного вида. Применительно к вышеизложенному частичную инвариантность следует трактовать как селективную абсолютную инвариантность, т.е. независимость xвын(t) на воздействие ψ(t) определенного вида. Рассмотрим количественные оценки инвариантности до ε. При полной неопределенности условий работы САУ предлагается использовать либо интегральную оценку вида
Показатели качества (количественные меры инвариантности) селективно инвариантных систем. Селективно абсолютно инвариантные системы имеют нулевую установившуюся ошибку по отношению к рассматриваемым воздействиям (g(t) или f(t)). В селективно инвариантных до ε системах значения отличных от нуля установившихся ошибок могут служить количественной мерой их инвариантности.
Можно
использовать оценку в виде
|
16. ОТУ - Устойчивость дискретных систем.
Необходимое
и достаточное условие устойчивости
дискретной линейной системы выражается
следующим неравенством:
Для
стационарной дискретной линейной
системы:
Следовательно, необходимым и достаточным условием устойчивости стационарной дискретной линейной системы является абсолютная сходимость ряда, членами которого являются ее весовые коэффициенты. Импульсная передаточная функция устойчивой системы конечна всюду вне единичного круга плоскости комплексной переменной z с центром в начале координат.
Таким
образом, для устойчивости стационарной
дискретной линейной системы необходимо
и достаточно, чтобы все полюсы ее
импульсной передаточной функции Ф(z)
лежали внутри единичного круга с
центром в начале координат. В некоторых
случаях импульсную передаточную
функцию Ф(z)
удобно рассматривать как функцию
параметра Отсюда следует, что к стационарным дискретным линейным системам применимы критерии устойчивости для непрерывных систем, но модифицированные с учетом особенностей описания дискретных систем.
Критерий
устойчивости Михайлова для дискретных
систем требует, чтобы годограф
Дискретное
уравнение движения в пространстве
состояний
Определения устойчивости:
1.
Решение
2.
Решение
Стационарная дискретная линейная система асимптотически устойчива тогда и только тогда, когда все собственные значения матрицы Ф лежат строго внутри единичного круга.
|
||||||||||||||||||||||||
|
17. ОТУ - Управляемость и наблюдаемость дискретных САУ. Управляемость связана с возможностью перевода системы из заданного начального состояния в любое другое, а наблюдаемость с возможностью определения состояния динамической системы по наблюдаемым входам и выходам.
Определение
управляемости.
Система
Матрицу M по аналогии с непрерывными системами называют матрицей управляемости. С управляемостью тесно связано понятие достижимости. Определение достижимости. Система достижима, если существует управляющая последовательность, переводящая систему из любого начального состояния в произвольное состояние за конечное время.
Управляемость
не означает достижимость. Если
Из определения достижимости следует, что система достижима тогда и только тогда, когда матрица M имеет ранг n. Матрица управляемости не зависит от выбора системы координат в пространстве состояний. Из приведенных выше определений следует, что можно найти такую управляющую последовательность, что любое состояние достигается не более чем за n шагов (тактов дискретной системы). |
18. ОТУ - Графовые модели дискретной нелинейной динамической системы. Изложим суть на примере дискретной нелинейной САУ
Д Обычно инерционный нелинейный объект естественно представить в виде последовательного соединения трех частей: входной линейной части ОУ линейного фильтра Л1, выход x которого поступает на нелинейный безынерционный преобразователь H, а его выходная величина F фильтруется линейным фильтром Л2. Предположим, что УУ дискретной системы реализует алгоритм
Построим графы для нескольких значений инерционности v. 1. Инерционность v=0 (рис. 1 а). Здесь нет необходимости в кодировании состояний двумя числами, поскольку каждое состояние системы определяется мгновенным значением управления, т.е. только одним числом i. Из состояния i возможны два перехода : в состояние (i-1) и в состояние (i+1).
2.
Инерционность v=1
(рис.
2 б).
Состояния кодируются парами ( 3. Инерционность v=2 (рис. 3 в). В системе возможны следующие переходы: из состояния (i, 0) в состояния (i+1,0) и (i-1,2); из состояния (i, 1) в состояния (i+1,0) и (i-1,2); из состояния (i, 2) в состояния (i+1,1) и (i-1,3); из состояния (i, 3) в состояния (i+1,1) и (i-1,3).
б)
в)
Рис. 3 Графы поведения дискретной системы Графовые модели являются достаточно мощным средством исследования дискретных САУ. Они наглядно иллюстрируют динамику системы и позволяют определить основные ее характеристики.
|
||||||||||||||||||||||||
|
19. ОТУ - Принцип максимума: геометрическая интерпретация, управление автономной системой. Геометрическая интерпретация принципа максимума Л.С. Понтрягина.
а) б)
Пусть стоит задача о переводе за минимальное время изображающей точки из некоторого начального состояния 0 в определенное конечное состояние K. Каждой точке фазового пространства, окружающего точку K, соответствует определенная оптимальная траектория и отвечающее ей минимальное время перехода в эту точку. Вокруг конечной точки можно построить поверхности, являющиеся геометрическим местом точек с одинаковым минимальным временем ti перехода в эту точку (рис.а) - изохроны. Оптимальная по быстродействию траектория из точки 0 в конечную точку K должна быть максимально близка нормалям к изохронам, т.е. должна приближаться к ним настолько близко, насколько это позволяют ограничения, налагаемые на координаты ОУ. Математически это условие оптимальности траектории означает, что на протяжении всей траектории скалярное произведение вектора скорости v=dy/dt на вектор, обратный градиенту времени перехода в конечную точку, должно быть максимально. Если обозначить это произведение через H, а вектор, обратный градиенту времени перехода, через ψ, т.е. ψ=-grad tn (рис.а), то можно записать:
Управление автономной системой. Система называется автономной, если правые части дифференциальных уравнений, описывающих ее движение, явно не зависят от времени.
Функционал
качества в этом случае выбирается в
виде интегрального выражения
Задача
оптимального управления сводится к
минимизации дополнительной координаты
|
20. ОТУ - Адаптивное управление: общие сведения, алгоритмы адаптации, дуальное управление.
Примем
описание управляемого объекта в виде
системы нелинейных разностных уравнений
в векторной форме::
Дуальное управление. Нельзя оптимально управлять объектом, не зная его характеристик, но можно изучать объект, управляя им, и тем самым иметь возможность улучшать управление, приближая его к оптимальному. В этой ситуации управляющие воздействия носят двойственный характер. Они служат как средством изучения, познавания объекта, так и средством направления его к желаемому (т.е. оптимальному) состоянию. Такое управление называют дуальным управлением. В системах дуального управления всегда существует противоречие между познавательной и направляющей сторонами управляющего воздействия. Очевидно, что двойственность знания и управления тесно связана с двойственностью прошлого и будущего. Алгоритмы «изучения» и «управления» тесно связаны между собой. Это говорит о том, что процессы изучения и управления неразрывны, в чем и состоит суть дуального управления. |

 .
. ,
где
,
где
 ,
, .
. и
т.д. по рекуррентной формуле для
и
т.д. по рекуррентной формуле для
 .
. (
( основу этого метода положен следующий
принцип оптимальности: любой
конечный участок оптимальной траектории
является тоже оптимальной траекторией,
т.е. часть оптимальной траектории от
любой промежуточной точки до ее конца
является оптимальной траекторией
между этими точками, если считать
данную промежуточную точку началом
траектории.
основу этого метода положен следующий
принцип оптимальности: любой
конечный участок оптимальной траектории
является тоже оптимальной траекторией,
т.е. часть оптимальной траектории от
любой промежуточной точки до ее конца
является оптимальной траекторией
между этими точками, если считать
данную промежуточную точку началом
траектории.
 (9.52)
(9.52) (9.63)
(9.63)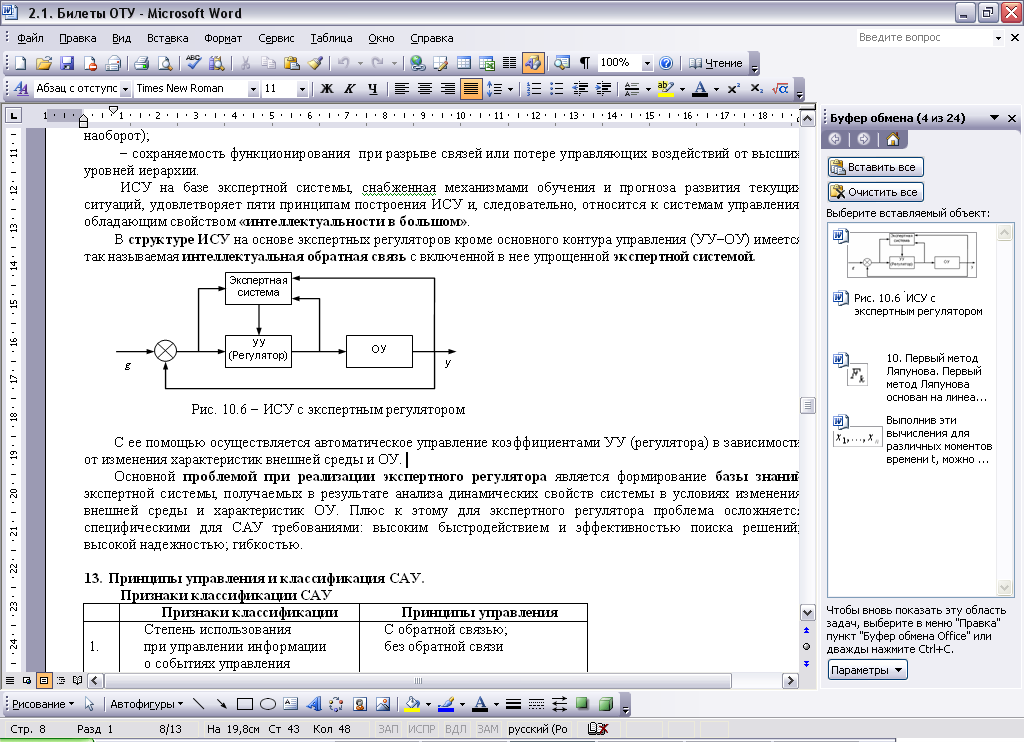 структуре таких ИСУ, так же, как и в
структуре адаптивных САУ, кроме
основного контура управления (УУОУ)
имеется так называемая интеллектуальная
обратная связь с включенной в нее
упрощенной экспертной системой.
Упрощение
заключается в ориентации экспертной
системы на решение управленческих
задач, а также в отсутствии некоторых
специфических блоков, присущих
экспертным системам более широкого
класса (например, подсистемам
объяснения). С помощью экспертной
системы осуществляется автоматическое
управление коэффициентами УУ
(регулятора) в зависимости от изменения
характеристик внешней среды и ОУ.
Основной проблемой при реализации
экспертного регулятора является
формирование базы знаний экспертной
системы, получаемых в результате
анализа динамических свойств системы
в условиях изменения внешней среды и
характеристик ОУ. Формирование базы
знаний и организация эффективных
механизмов вывода необходимы при
разработке любой экспертной системы.
Однако для экспертного регулятора
проблема осложняется специфическими
для САУ требованиями: высоким
быстродействием и эффективностью
поиска решений, удовлетворяющих целям
управления; высокой надежностью
(способностью обеспечивать эффективное
функционирование системы управления
в условиях не полностью определенной
входной информации); гибкостью
(способностью к подключению различных
механизмов вывода на соответствующих
фрагментах знаний) и компактностью
(малыми массогабаритными характеристиками
устройств, реализующих функции
экспертной системы).
структуре таких ИСУ, так же, как и в
структуре адаптивных САУ, кроме
основного контура управления (УУОУ)
имеется так называемая интеллектуальная
обратная связь с включенной в нее
упрощенной экспертной системой.
Упрощение
заключается в ориентации экспертной
системы на решение управленческих
задач, а также в отсутствии некоторых
специфических блоков, присущих
экспертным системам более широкого
класса (например, подсистемам
объяснения). С помощью экспертной
системы осуществляется автоматическое
управление коэффициентами УУ
(регулятора) в зависимости от изменения
характеристик внешней среды и ОУ.
Основной проблемой при реализации
экспертного регулятора является
формирование базы знаний экспертной
системы, получаемых в результате
анализа динамических свойств системы
в условиях изменения внешней среды и
характеристик ОУ. Формирование базы
знаний и организация эффективных
механизмов вывода необходимы при
разработке любой экспертной системы.
Однако для экспертного регулятора
проблема осложняется специфическими
для САУ требованиями: высоким
быстродействием и эффективностью
поиска решений, удовлетворяющих целям
управления; высокой надежностью
(способностью обеспечивать эффективное
функционирование системы управления
в условиях не полностью определенной
входной информации); гибкостью
(способностью к подключению различных
механизмов вывода на соответствующих
фрагментах знаний) и компактностью
(малыми массогабаритными характеристиками
устройств, реализующих функции
экспертной системы).

 управляема, если существует управляющая
последовательность, переводящая
систему из любого начального состояния
в начало координат за конечное время.
управляема, если существует управляющая
последовательность, переводящая
систему из любого начального состояния
в начало координат за конечное время. искретная
нелинейная САУ
искретная
нелинейная САУ а)
а)


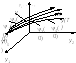
 ,
где
,
где
 ,
удовлетворяющей условию
,
удовлетворяющей условию