Принцип максимума и вариационное исчисление

Рассмотрим стандартную задачу вариационного исчисления найти

при условии и одном из условий:

а) ;

б) ;

в) конец не закреплён.

Преобразуем её в задачу оптимального управления, положив

. Поскольку в исходной задаче условия на не накладывались, нет условий и на управление, поэтому . Функция Понтрягина имеет вид

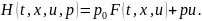
Согласно принципу максимума, если есть решение задачи, то , как функция от , максимизируется при Ввиду того, что необходимым условием максимума является

(20)

Если бы то из (20) следовало бы, что что противоречит условию Поэтому и

. (21)

Дифференцируя обе части равенства (20) по , получаем

. (22)

Из (21) и (22), с учётом равенства получаем

,

что представляет собой уравнение Эйлера. Из (20) следует, что

. (22)

Напомним, что условия трансверсальности в задаче управления имели вид:

Б) причём , если ;

В) .

В задаче вариационного исчисления они имели вид, соответственно:

причём , если ;

в случае незакреплённого конца

Формула (22) подтверждает совпадение этих условий.

Пример. Решить двумя способами задачу найти

Первое решение. Выписываем уравнение Эйлера:

, , ,

откуда

т.е. ,

Условие даёт условие даёт

Ввиду того. Что подынтегральная функция выпукла вверх, решение найдено.

Второе решение. Решим задачу методом теории оптимального управления.

Переформулируем её следующим образом: найти

Функция Понтрягина имеет вид

следовательно,

(23)

. (24)

Равенства (23),(24) и условие дают систему уравнений

Продифференцируем первое уравнение и используем второе уравнение:

откуда и

Снова условие даёт условие даёт При этом

2 .

Задача. Решить задачу найти

двумя способами: используя уравнение Эйлера и используя принцип максимума.

§4.Сопряжённая функция, как скрытая цена

Снова рассмотрим задачу найти

при условиях

,

и одном из условий:

а)

б)

в) конец не закреплён.

Предположим, что найдена единственная оптимальная пара и единственная ответствующая сопряжённая функция .

Обозначим

и назовём её оптимальным значением целевой функции. Эта функция, вообще горя, не дифференцируемая. Однако тех точках, где она дифференцируема, справедливо равенство

.

Мы не будем приводить доказательства этой формулы, а рассмотрим пример, её подтверждающий. Выше была решена следующая задача.

Задача. Найти

конец не закреплён.

При её решении было получено:

.

.

Таким образом, имеется единственная пара функций и сопряжённая функция дающие решение задачи.

При этом

.

Используем правило Лейбница дифференцирования собственного интеграла по параметру и найдём

Подставляя в формулу , получаем тот же результат.

Снова рассмотрим сформулированную в начале параграфа задачу и предположим, что все допустимые имеют скачок в точке и непрерывны в остальных точках этого интервала. Пусть оптимальная пара для случая Тогда, при определённых условиях, можно доказать, что дифференцируема по в точке причём

(25)

Пусть обозначает уровень прибыли в момент , обозначает величину капитала, управление, которое изменяется в пределах . Скорость изменения капитала зависит от , что выражается уравнением .

Согласно (25), представляет собой «скрытую цену» капитала, поскольку измеряет предельную прибыль.

Если рассмотреть небольшой отрезок времени , то . Следовательно,

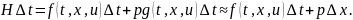
Принцип максимума требует выбирать в любой момент времени такое управление которое максимизирует Положим

.

Можно доказать, что

.