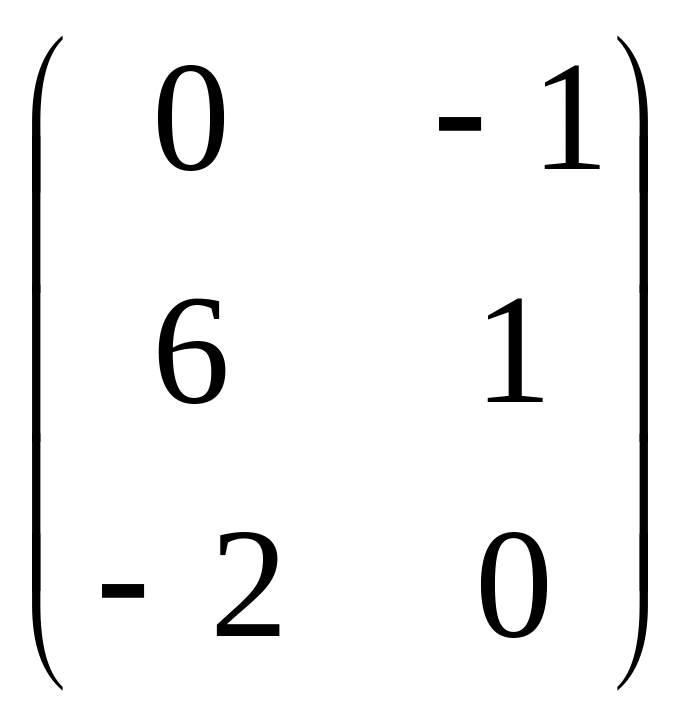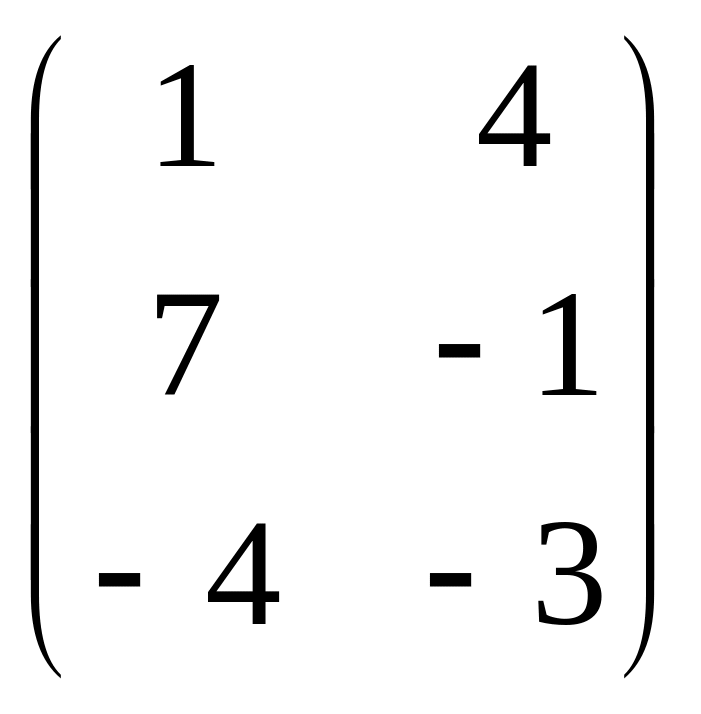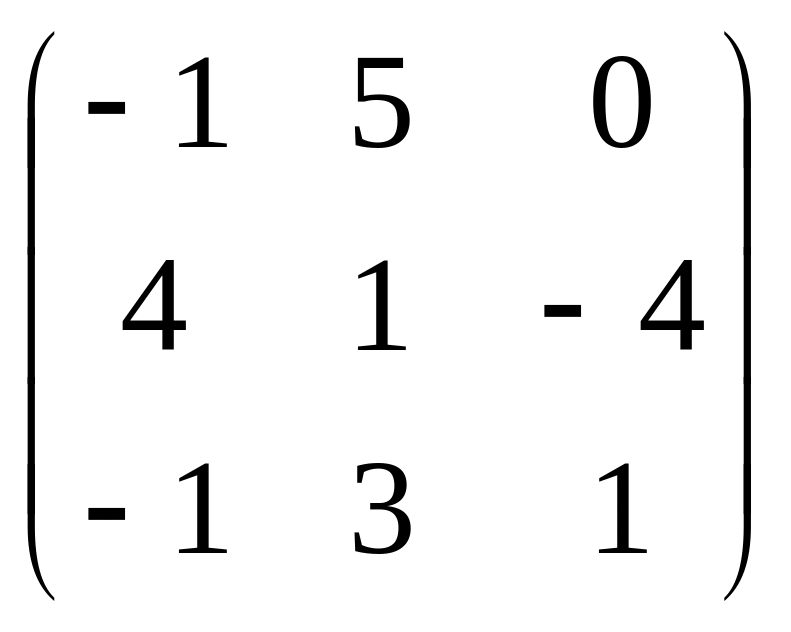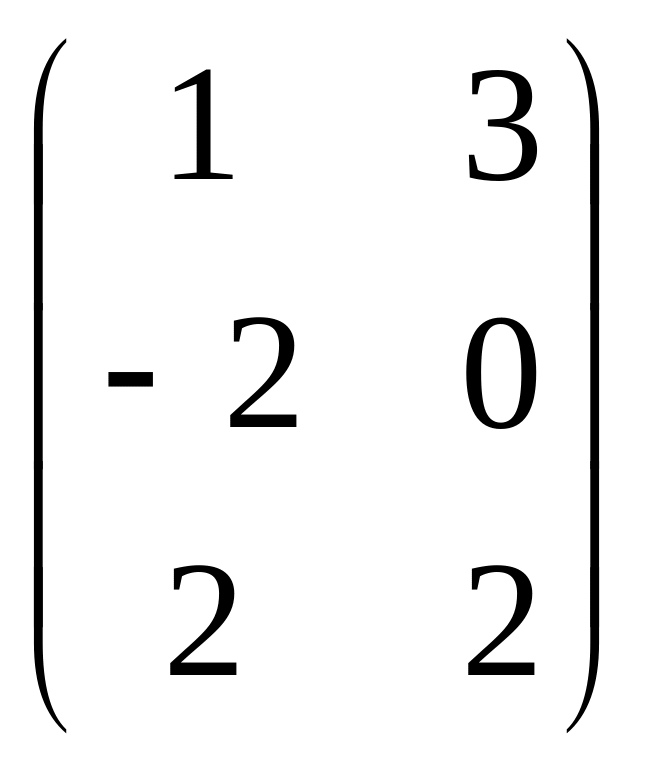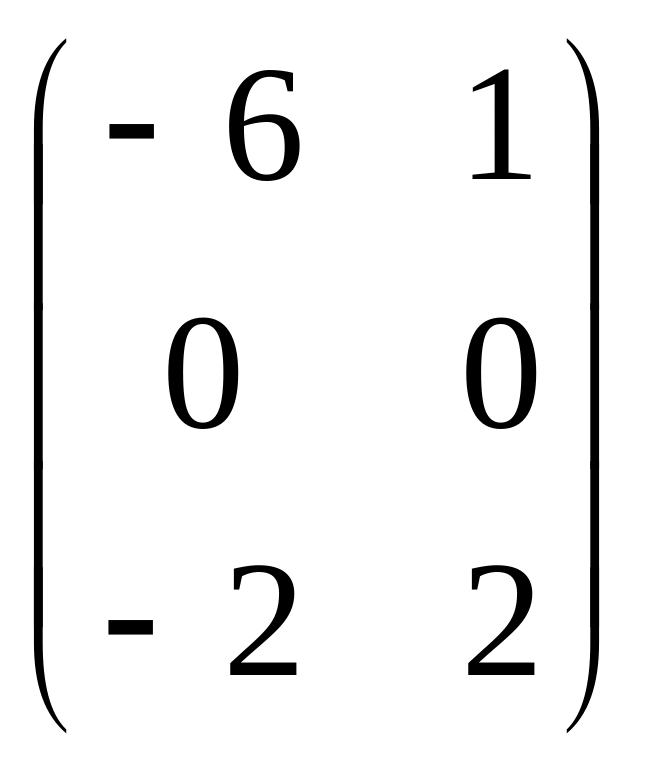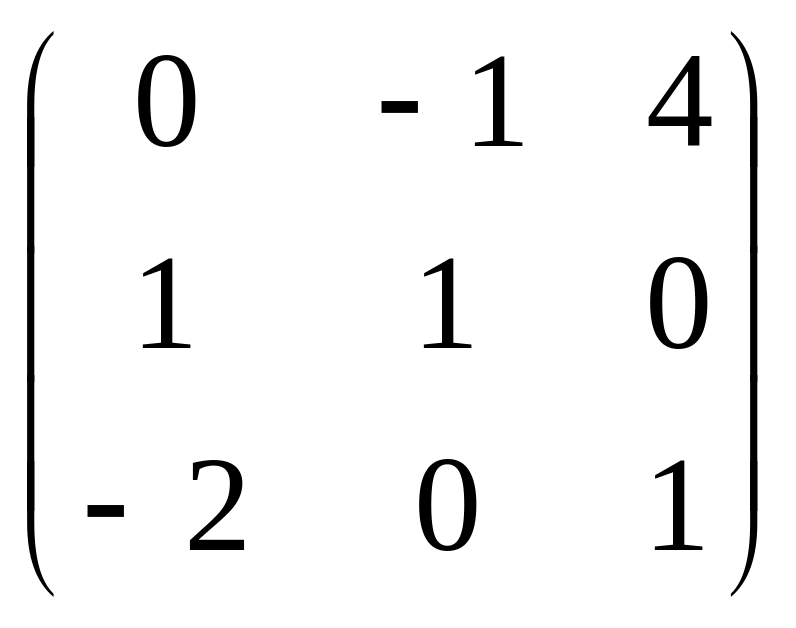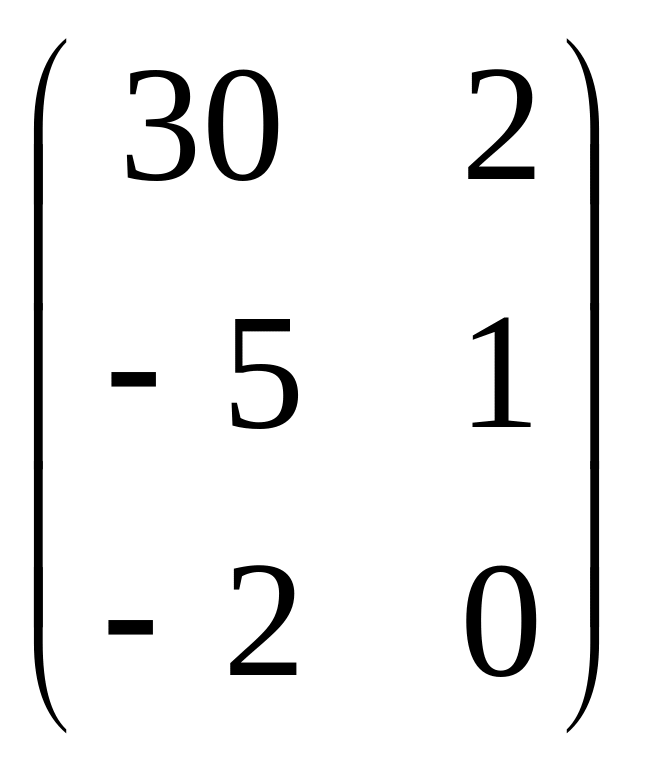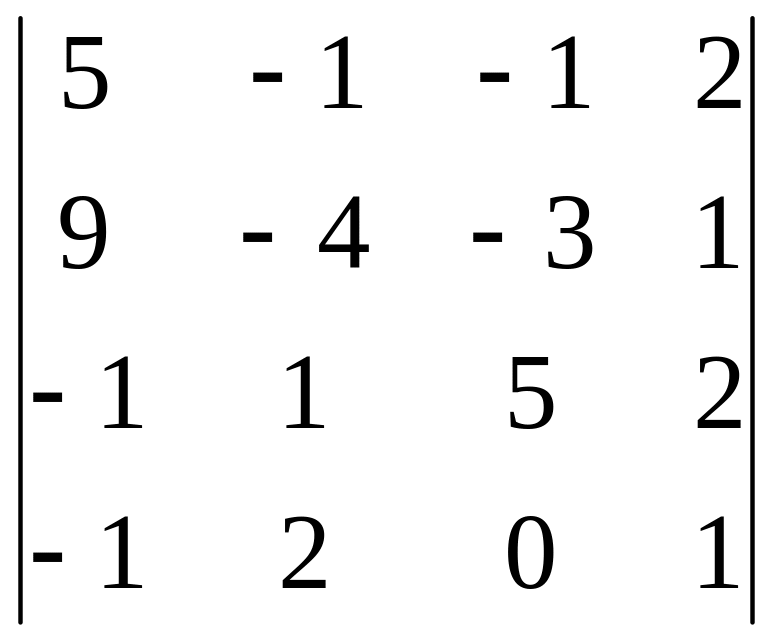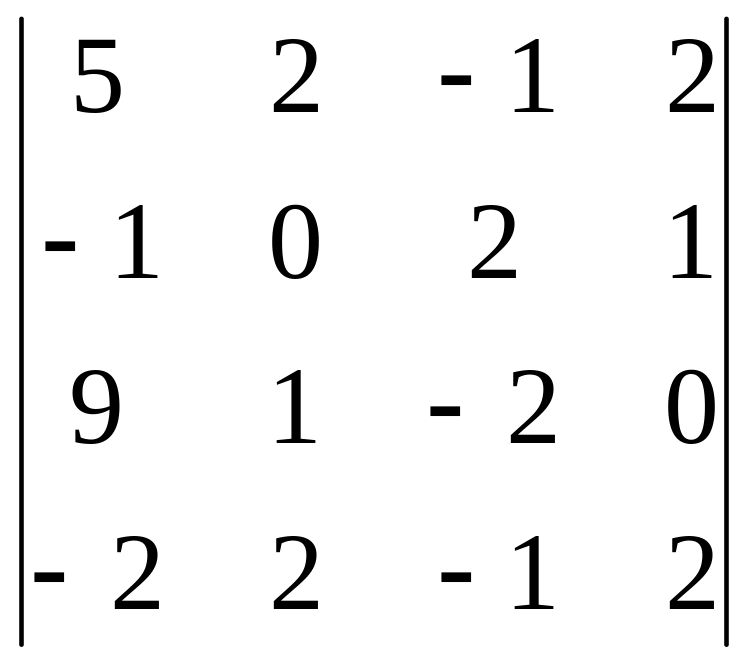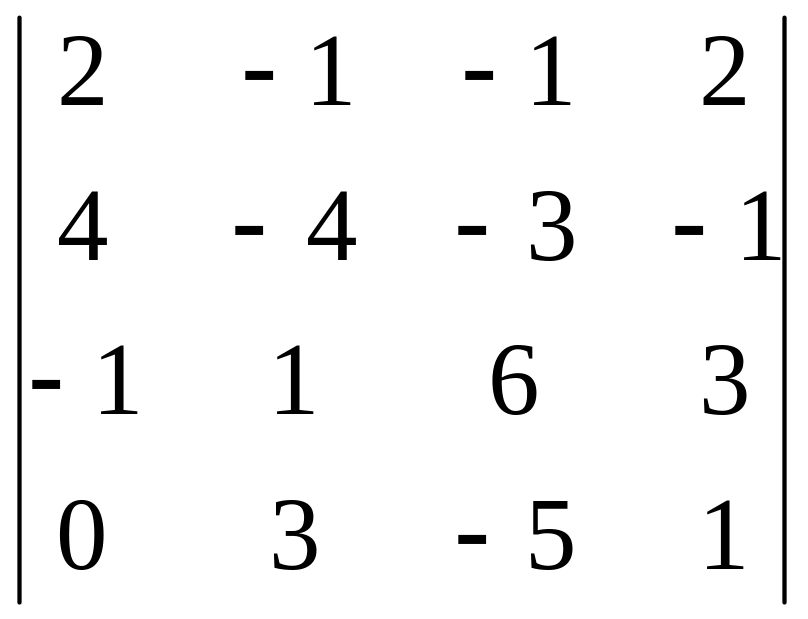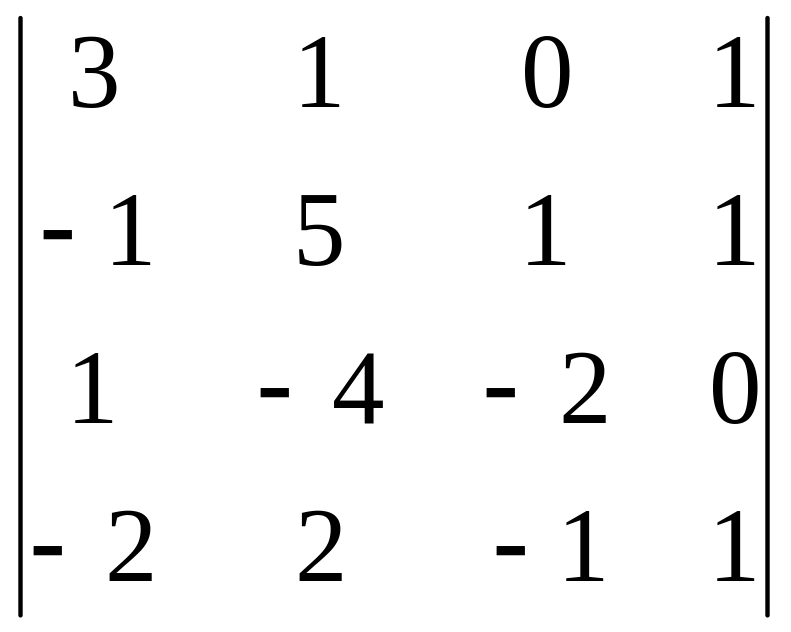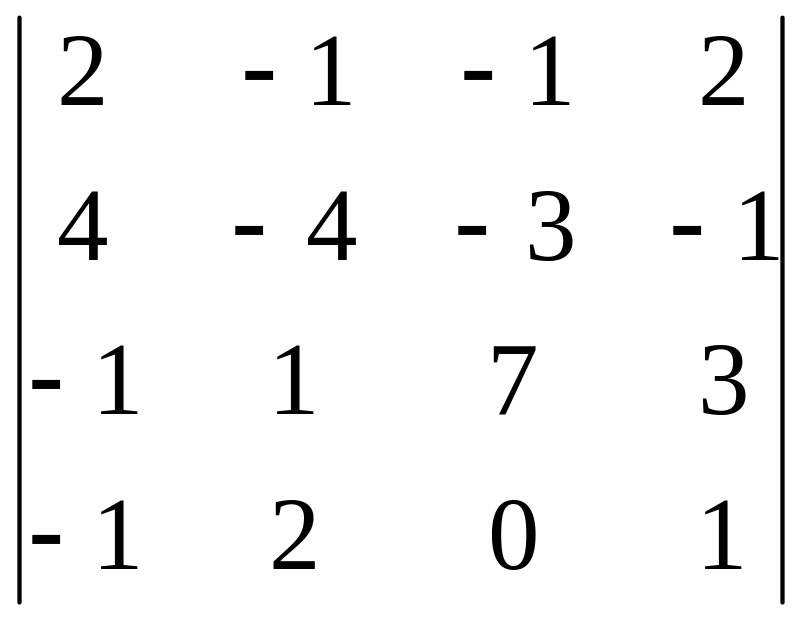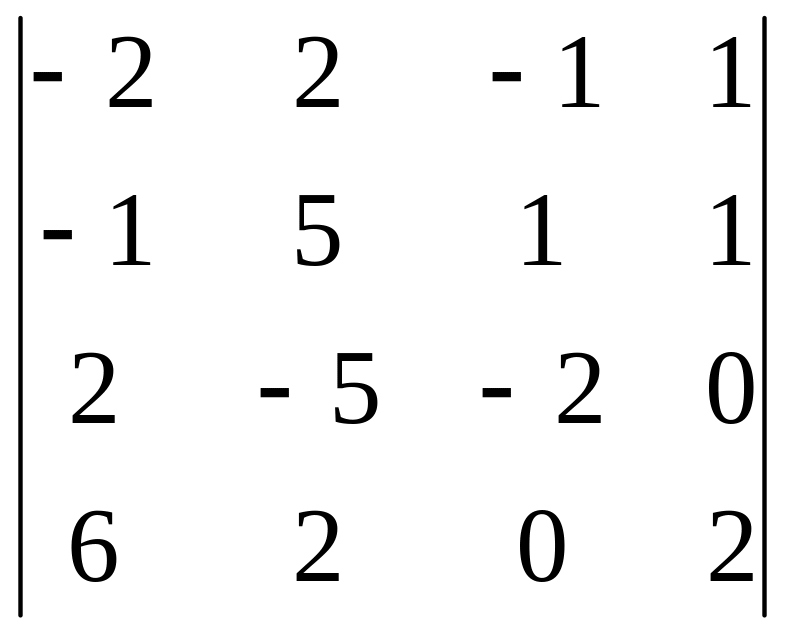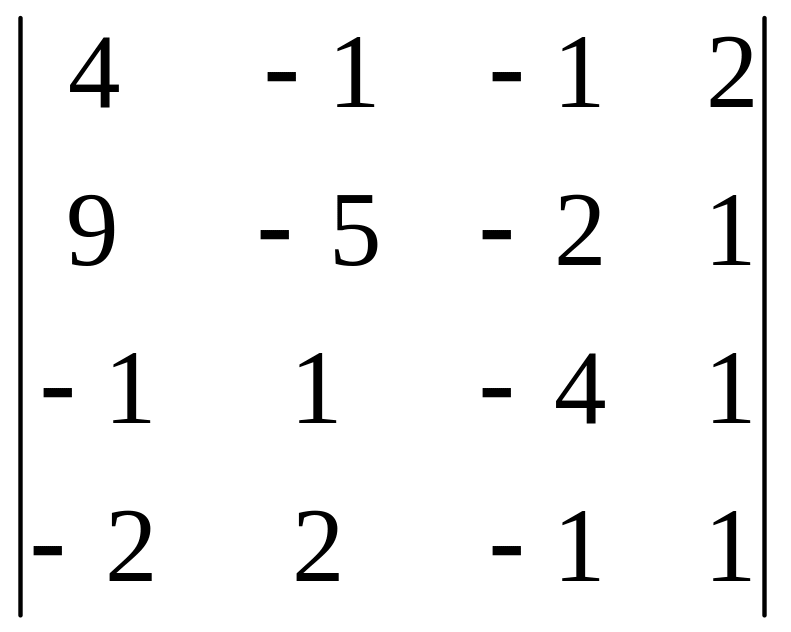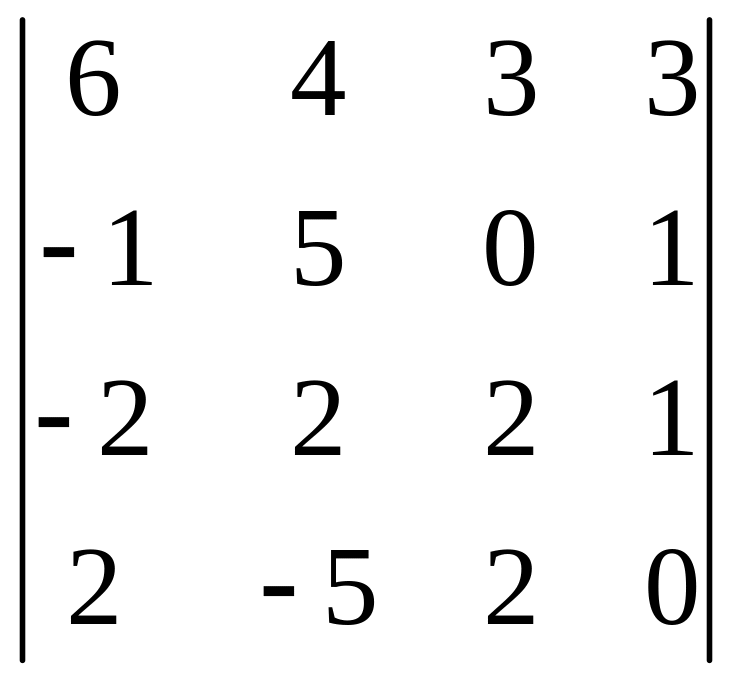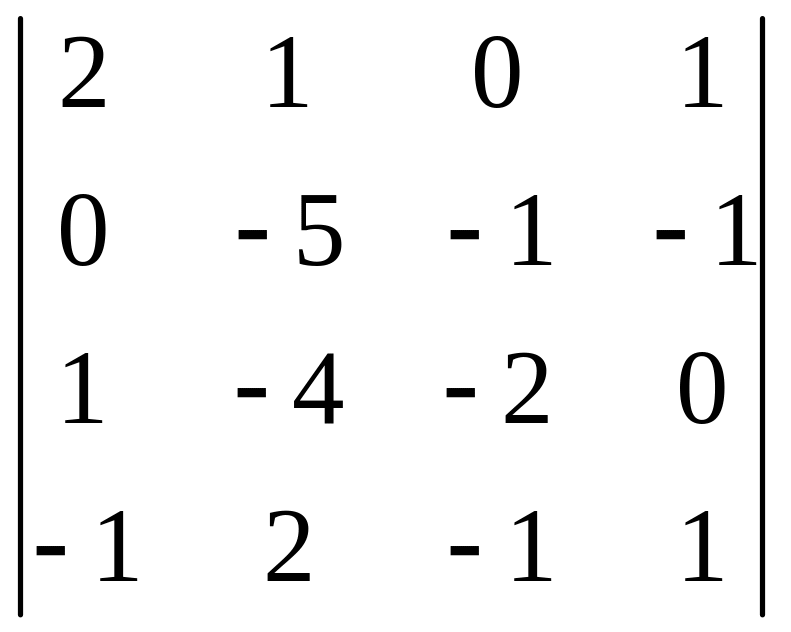Практические задания
Задание 1
Найти
значение выражения
![]() ,
если n
нечетно,
,
если n
нечетно,
и
значение выражения
![]() ,
если n
четно.
,
если n
четно.
Матрицы А, В, С взять из таблицы 1 согласно числу n, которое определяется номером студента по списку в журнале.
Таблица 1
n |
A |
B |
C |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
Продолжение таблицы 1
n |
A |
B |
C |
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
Продолжение таблицы 1
n |
A |
B |
C |
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
Продолжение таблицы 1
n |
A |
B |
C |
29 |
|
|
|
30 |
|
|
|
31 |
|
|
|
32 |
|
|
|
33 |
|
|
|
34 |
|
|
|
35 |
|
|
|
36 |
|
|
|
37 |
|
|
|
38 |
|
|
|
Продолжение таблицы 1
n |
A |
B |
C |
39 |
|
|
|
40 |
|
|
|
41 |
|
|
|
42 |
|
|
|
43 |
|
|
|
44 |
|
|
|
45 |
|
|
|
46 |
|
|
|
47 |
|
|
|
Продолжение таблицы 1
n |
A |
B |
C |
48 |
|
|
|
49 |
|
|
|
50 |
|
|
|
Задание 2
Найти определитель матрицы А по правилу треугольников.
Матрицу А взять из таблицы 2.
Таблица 2
n |
A |
B |
n |
A |
B |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
Продолжение таблицы 2
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
|
26 |
|
|
Продолжение таблицы 2
n |
A |
B |
n |
A |
B |
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|
|
31 |
|
|
32 |
|
|
33 |
|
|
34 |
|
|
35 |
|
|
36 |
|
|
37 |
|
|
38 |
|
|
39 |
|
|
40 |
|
|
41 |
|
|
42 |
|
|
43 |
|
|
44 |
|
|
Продолжение таблицы 2
n |
A |
B |
n |
A |
B |
45 |
|
|
46 |
|
|
47 |
|
|
48 |
|
|
49 |
|
|
50 |
|
|
Задание 3
Найти
матрицу, обратную матрице А.
Проверить, что
![]()
Матрицу А взять из таблицы 2.
Задание 4
Записать систему линейных уравнений, соответствующую уравнению в матричной форме:
![]() ,
где
,
где
 .
.
Решить полученную систему методом Крамера.
Матрицы А и В взять из таблицы 2. Значение главного определителя матрицы взять из решения задания 2.
Задание 5
Полученную в задании 4 систему линейных уравнений решить методом обратной матрицы.
Обратную матрицу взять из решения задания 3.
Задание 6
Полученную в задании 4 систему линейных уравнений решить методом Гаусса.
Задание 7
Вычислить определитель 4-го порядка, пользуясь элементарными преобразованиями.
Определитель взять из таблицы 3
Таблица 3
n |
|
n |
|
n |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
Продолжение таблицы 3
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
26 |
|
27 |
|
28 |
|
29 |
|
30 |
|
31 |
|
32 |
|
33 |
|
Продолжение таблицы 3
34 |
|
35 |
|
36 |
|
37 |
|
38 |
|
39 |
|
40 |
|
41 |
|
42 |
|
43 |
|
44 |
|
45 |
|
46 |
|
47 |
|
48 |
|
49 |
|
50 |
|
|
|
Задание 8
Выразить матрицу Х через матрицы А, В,C и D из матричного уравнения. Найти матрицу Х.
Матричное уравнение и матрицы А, В и С приведены в таблице 4
Таблица 4
n |
Матричное уравнение |
А |
В |
С |
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
14 |
|
|
|
|
Продолжение таблицы 4
n |
Матричное уравнение |
А |
В |
С |
15 |
|
|
|
|
16 |
|
|
|
|
17 |
|
|
|
|
18 |
|
|
|
|
19 |
|
|
|
|
20 |
|
|
|
|
21 |
|
|
|
|
22 |
|
|
|
|
23 |
|
|
|
|
24 |
|
|
|
|
25 |
|
|
|
|
26 |
|
|
|
|
27 |
|
|
|
|
Продолжение таблицы 4
n |
Матричное уравнение |
А |
В |
С |
28 |
|
|
|
|
29 |
|
|
|
|
30 |
|
|
|
|
31 |
|
|
|
|
32 |
|
|
|
|
33 |
|
|
|
|
34 |
|
|
|
|
35 |
|
|
|
|
36 |
|
|
|
|
37 |
|
|
|
|
38 |
|
|
|
|
39 |
|
|
|
|
40 |
|
|
|
|
Продолжение таблицы 4
n |
Матричное уравнение |
А |
В |
С |
41 |
|
|
|
|
42 |
|
|
|
|
43 |
|
|
|
|
44 |
|
|
|
|
45 |
|
|
|
|
46 |
|
|
|
|
47 |
|
|
|
|
48 |
|
|
|
|
49 |
|
|
|
|
50 |
|
|
|
|