2.7 Расчет коэффициента стоячей волны

Произвольная нагрузка в общем случае порождает в линии передачи отраженную волну. Накладываясь на падающую, отраженная волна приводит к образованию повторяющихся максимумов и минимумов в продольных распределениях нормированных токов и напряжений, формируя картину смешанных волн. Режим смешанных волн в инженерной практике принято характеризовать коэффициентом бегущей волны (КБВ), представляющим собой отношение минимального значения нормированного полного напряжения (или тока, или напряженности) в линии к максимальному значению полного напряжения (или тока, или напряженности поля) в линии

где |Г| - модуль коэффициента отражения. Часто вместо КБВ пользуются обратной ему величиной, называемой коэффициентом стоячей волны (КСВ)

Коэффициентом отражения называется отношение поперечных компонентов электрического поля для падающей и отраженной волн в одной и той же точке поперечного сечения линии передачи

где Z_A – входное сопротивление антенны,

Z_В – волновое сопротивление линии передачи (коаксиального кабеля). Зависимость входного сопротивления от частоты рассчитана в предыдущем пункте.

По методу излучаемой мощности получаем

По методу наведенных ЭДС получаем

График зависимости КСВ от длины волны приведен в приложении В.

2.8 Расчет ппф и его ачх

Фильтры СВЧ применяют для частотной селекции сигналов, согласования комплексных нагрузок, в цепях задержки и в качестве замедляющих систем.

Фильтры являются обычно пассивными взаимными устройствами и характеризуются частотной зависимостью вносимого в тракт затухания. Полоса частот с малым затуханием называется полосой пропускания, а полоса частот с большим затуханием – полосой заграждения. По взаимному расположению полосы пропускания и заграждения принято выделять следующие типы фильтров: фильтр нижних частот (ФНЧ), пропускающие сигналы ниже заданной граничной частоты и подавляющие сигналы с частотами выше граничной; фильтры верхних частот (ФВЧ), пропускающие сигналы на частотах выше заданной и подавляющие сигналы других частот; полосно-пропускающие (полосовые) фильтры (ППФ), пропускающие сигналы в пределах заданной полосы частот и подавляющие сигналы вне этой полосы, полосно-заграждающие (режекторные) фильтры (ПЗФ), подавляющие сигналы в пределах заданной полосы частот и пропускающие сигналы вне этой полосы.

Частотная характеристика каждого фильтра имеет переходную область между полосой пропускания и полосой заграждения, то есть между частотами _з и _п. В этой области затухание меняется от максимального значения до минимального. Обычно стараются уменьшить эту область, что приводит к усложнению фильтра, увеличению числа его звеньев. При проектировании фильтров, как правило, задаются следующие характеристики: полоса пропускания, полоса заграждения, средняя частота, затухание в полосе пропускания, затухание в полосе заграждения, крутизна изменения затухания в переходной области, уровень согласования по входу и по выходу, характеристики линии передачи, в которую включается фильтр, тип линии передачи, иногда оговариваются фазовые характеристики фильтра.

В данной работе необходимо рассчитать ППФ пропускающий дециметровые каналы с 21 по 29. На граничных частотах диапазона L_п=3дБ, при расстройке на 20МГц L_з=20дБ. Исходные данные занесем в таблицу 2.4.

fп,МГц	f-п,МГц	Lп,дБ	fз,МГц	f-з,МГц	Lз,дБ
543	470	3	563	450	20

Таблица 2.4 – Исходные характеристики ППФ

2.8.1 Расчет низкочастотного фильтра прототипа

В настоящее время наиболее распространенной методикой расчета фильтров СВЧ является методика, согласно которой вначале рассчитывается низкочастотный фильтр-прототип. Нахождение параметров схемы фильтра-прототипа по заданной частотной характеристике фильтра является задачей параметрического синтеза. Для общности результатов все величины нормируются. Сопротивления нагрузки и генератора принимается равным единице. Наряду с нормировкой по сопротивлению проводится нормировка по частоте, например граничная частота полосы пропускания фильтра принимается равным единице. Таким образом расчет фильтра СВЧ сводится к синтезу схемы НЧ-прототипа и замене элементов с сосредоточенными параметрами их эквивалентами с распределенными параметрами.

Для аппроксимации частотных характеристик применяется ряд функций, удовлетворяющих условиям физической реализуемости фильтров. Наиболее распространенной являются максимально плоская и равноволновая аппроксимации, использующие полиномы Баттерворта и Чебышева соответственно.

Рассчитаем фильтр с максимально плоской характеристикой затухания. Она монотонно возрастает при повышении частоты:

,

где n – число звеньев фильтра прототипа,

=/_п – нормированная частота,

=10^Lп/10-1 – коэффициент пульсаций,

_п – граничная частота полосы пропускания,

L_п – затухание на частоте _п (см рисунок 2.3).

Рисунок 2.3 – Максимально плоская характеристика затухания фильтра-прототипа нижних частот

Число звеньев фильтра прототипа может быть найдено из требований к АЧХ фильтра. Так , для фильтра с максимально плоской АЧХ:

,

то есть для нашего фильтра необходимо, чтобы n2.76.

Возьмем n=3, тогда схема фильтра-прототипа будет иметь вид, изображенный на рисунке 2.4

Рисунок 2.4 – Схема фильтра-прототипа нижних частот

Параметры фильтра можно рассчитать по сложным формулам, а можно воспользоваться справочной литературой, например [7]: g₀=1, g₁=0.999165, g₂=1.998330, g₃=0.999165, g₄=1.

Денормировки параметров фильтра производится с помощью соотношений

,

,

.

Здесь обозначения со штрихом относятся к нормированным параметрам фильтра-прототипа, без штрихов к денормированным: R₀`=1, L<sub>1</sub>`=1, C₂`=2, L<sub>3</sub>`=1, R₄`=1.

Так как будущий фильтр будем ставить в коаксиальный тракт передачи, то R₀=75Ом, тогда

2.8.2 Расчет ППФ

Для проектирования ППФ воспользуемся фильтром-прототипом, рассчитанным в предыдущем пункте и реактансное преобразование частоты

где ₀=(_п_-п)^0.5 – центральная частота ППФ,

k_з=1/2 - коэффициент преобразования,

2=_п-_-п – полоса пропускания ППФ.

Любая индуктивность в фильтре прототипе после выполнения частотного преобразования трансформируются в последовательный контур с параметрами

Одновременно любая емкость в фильтре прототипе превращается в параллельный колебательный контур

Рисунок 2.5 – Эквивалентная схема ППФ

Таким образом, ППФ (рисунок 2.5) состоит из каскадно-включенных резонаторов, значения эквивалентных параметров которого получились следующими

2.8.3 Реализация ППФ

По способу реализации ППФ можно разделить на следующие типы: на одиночной МПЛ с зазорами, на параллельных связанных полуволновых резонаторах, на встречных стержнях, с параллельными и последовательными четвертьволновыми шлейфами длиной /4, где  - длина волны в линии, соответствующая средней частоте полосы пропускания ППФ; с двойными шлейфами и четвертьволновыми соединительными линиями на диэлектрических резонаторах.

Выполним ППФ на микрополосковых линиях (МПЛ) с двойными шлейфами и четвертьволновыми соединительными линиями.

МПЛ представляют собой тонкий слой металла, нанесенного на листы диэлектрика. Наиболее распространены экранированные несимметричные МПЛ. МПЛ используются во всем диапазоне СВЧ. По сравнению с прямыми волноводами МПЛ обладают рядом недостатков – имеют более высокие погонные потери и сравнительно низкую передаваемую мощность. Кроме того, открытые МПЛ излучают энергию в пространство, из-за чего могут возникать нежелательные электромагнитные связи.

Но МПЛ обладают и важными достоинствами. Они имеют малые габариты и массу, дешевы в изготовлении, технологичны и удобны для массового производства методами интегральной технологии, что позволяет реализовать на пластине из металлизированного с одной стороны диэлектрика целые узлы и функциональные модули в микрополосковом исполнении.

Реализация последовательных колебательных контуров в МПЛ очень затруднена. Вместе с тем можно последовательное включение перевести в параллельное так, как это показано на рисунке 2.6 с помощью преобразований

Рисунок 2.6 Замена последовательного колебательного контура параллельным

Тождество на рисунке 2.6 выполняется только на резонансной частоте, поэтому получившуюся схему следует подвергать анализу для определения ее частотных свойств.

После замены получим схему ППФ изображенную на рисунке 2.7

Рисунок 2.7 – Эквивалентная схема ППФ

Эта схема имеет следующие значения параметров

Длина соединительной линии будет известна после определения параметров МПЛ.

Для расчета волнового сопротивления МПЛ воспользуемся выражением, полученным в квазистатическом приближении

(2.1)

Точность определения по этой формуле составляет 1% при w/h0.4 и 3% при w/h<0.4.

Для расчета длины волны на низких частотах на практике широко используется формула, также полученная в квазистатическом приближении

где  - длина волны в свободном пространстве,

_э – эффективная диэлектрическая проницаемость линии.

Эффективная диэлектрическая проницаемость может быть вычислена по формуле

, (2.3)

Подложку выполним на диэлектрике с относительной диэлектрической проницаемостью =7, а толщину подложки примем h=5мм. Ширина металлической полоски w, а соответственно и отношение w/h ,будут меняться при расчетах.

Сначала рассчитаем параметры соединительных линий. Для согласования фильтра с трактом передачи его соединительные линии должны иметь волновое сопротивление равное волновому сопротивлению коаксиала Z₀=75Ом. Разрешая выражение (2.1) находим, что w/h=0.5, тогда ширина полоски w=0.55=2.5(мм). По формуле (2.3) находим эффективную диэлектрическую проницаемость

Расчет ведем на средней частоте диапазона, поэтому ₀=0.594м, тогда по (2.2) длина волны в линии

Так как соединительная линия четвертьволновая, то ее длину определим по формуле

Параллельная индуктивность реализуется в виде короткозамкнутого параллельного шлейфа. Реактивное сопротивление такого отрезка линии определяется по формуле

(2.4)

Сопротивление этого шлейфа на средней частоте диапазона должно равняться сопротивлению параллельно включенной индуктивности, поэтому можно определить длину отрезка

(2.5)

Примем w/h=1(w=5мм), тогда по (2.1)-(2.3) получаем

Теперь по формуле (2.5) можно определить длину шлейфов, заменяющих каждую индуктивность

Параллельная емкость реализуется в виде параллельного шлейфа разомкнутого на конце. Реактивное сопротивление такого отрезка линии определяется по формуле

Сопротивление этого шлейфа на средней частоте диапазона должно равняться сопротивлению параллельно включенной емкости, поэтому можно определить длину шлейфа

(2.6)

Примем w/h=0.2(w=1мм), тогда по (2.1)-(2.3) получаем

Теперь по формуле (2.5) можно определить длину шлейфов, заменяющих каждую емкость

Занесем параметры шлейфов в таблицу 2.5.

	L1	L2	L3	C1	C2	C3	Соединительная линия
Ширина шлейфа, мм	5	5	5	1	1	1	2.5
Длина шлейфа, мм	4.7	2.4	4.7	28	29	28	35

Таблица 2.5 Размеры ППФ на МПЛ

Схема ППФ приведена в приложении Д.

2.8.4 Расчет АЧХ

АЧХ фильтра – это есть зависимость вносимого в тракт затухания от частоты. Зная входное сопротивление фильтра можно определить коэффициент отражения

(2.7)

Тогда АЧХ будет иметь следующий вид

(2.8)

Определим АЧХ низкочастотного фильтра прототипа изображенного на рисунке 2.4 после денормировки параметров

Подставляя в (2.7) и (2.8) получим характеристику затухания.

Определим АЧХ эквивалентной схемы ППФ изображенной на рисунке 2.5

где

Подставляя в (2.7) и (2.8), получим необходимую характеристику затухания.

Теперь определим АЧХ фильтра на МПЛ. Зависимость от частоты сопротивлений индуктивных и емкостных шлейфов определяется формулами

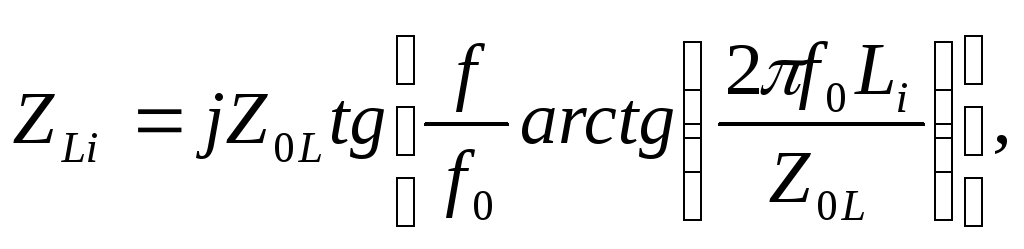
где i=1,2,3;

Z_0L и Z_0C – волновые сопротивления индуктивных и емкостных шлейфов соответственно.

Входное сопротивление фильтра

где

Конечная формула для входного сопротивления имеет очень сложный вид, поэтому не будем ее здесь приводить. По формулам (2.7) и (2.8) получим АЧХ.

Все АЧХ полученные в этом пункте приведены в приложении Г.