2.1.1. Определение угла раскрыва параболоида

После выбора излучателя следует найти соотношение между радиусом параболоида

определим из следующего соотношения и фокусным расстоянием(рис. 2.1) при помощи выражения

(2.1.4)

Рис. 2.1

Чтобы определить угол раскрыва выбирается в пределах, выберем его равным 0.5, тогда

С помощью выражений (2.1.2),(2.1.3) получим следующие уравнения

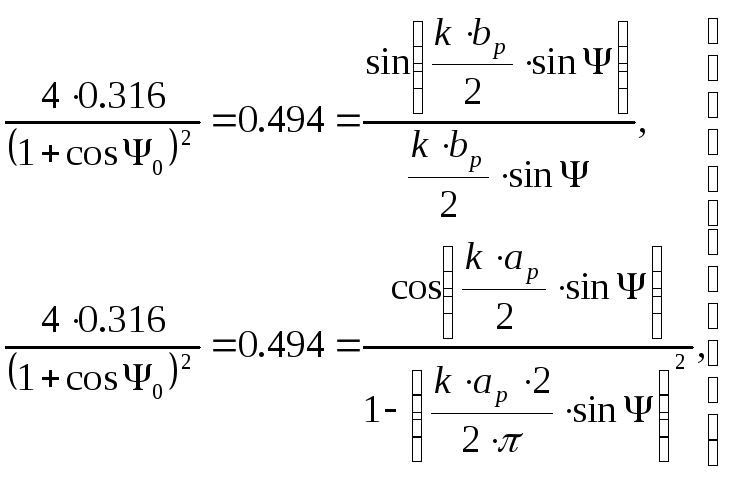
(2.1.5)

Решим уравнения (2.1.5) с помощью графиков функций (рис. 2.2)

Рис. 2.2 Графики функций

откуда

2.2 Расчет параболоида.

2.2.1 Определение диаметра параболоида 2Rп и фокусного расстояния f

Из приближенной формулы для КНД найдем радиус параболоида R_п

(2.2.1)

где - площадь раскрывa парабалоида.

(2.2.2)

Следовательно,

Фокусное расстояние можно определить пользуясь формулой

(2.2.3)

Диаметр парабалоида связан с заданной длиной волныи требуемым углом раствора диаграммы направленности на уровне половинной мощности (2_0.5) приближенной зависимостью

(2.2.4)

Тогда

2.3 Расчет диаграммы направленности.

Используя формулы (2.1.3) построим нормированную диаграмму направленности облучателя.

Рис. 2.3.1. Диаграмма направленности облучателя в полярной системе координат

Найдем распределение поля в раскрыве параболоида, для этого воспользуемся следующей формулой

(2.3.1)

где .

Полученные данные занесем в таблицу 2.3.1.

Таблица 2.3.1

	sin()	cos()						F(R)	F1(R)	F2(R)
0 5,3 10,6 15,9 21,2 26,5 31,8 37,1 42,4 47,7	0 0.092 0.184 0.274 0.362 0.446 0.527 0.603 0.674 0.74 0.799	1 0.996 0.983 0.962 0.932 0.895 0.85 0.798 0.738 0.673 0.602	0.54 0.541 0.545 0.551 0.559 0.57 0.584 0.601 0.621 0.646 0.674	1 0.998 0.991 0.981 0.966 0.947 0.925 0.899 0.869 0.837 0.801	1 0.99 0.961 0.914 0.853 0.782 0.705 0.625 0.547 0.473 0.405	0 0.05 0.1 0.151 0.202 0.254 0.308 0.362 0.419 0.477 0.538	0 0.093 0.186 0.279 0.374 0.471 0.57 0.671 0.776 0.884 0.997	1 0.988 0.953 0.897 0.825 0.741 0.652 0.562 0.475 0.396 0.325	1 0.994 0.977 0.947 0.905 0.85 0.781 0.696 0.594 0.472 0.329	1 0.988 0.954 0.899 0.824 0.734 0.633 0.529 0.432 0.357 0.325

Рис. 2.3.2 Распределение поля на раскрыве рупора

По найденному распределению поля на раскрыве вычисляется диаграмма направленности зеркальной антенны . Картина распределения поля на раскрыве зеркала может быть аппроксимирована при помощи соотношения:

(2.3.2)

где - равномерная часть распределения поля;

- неравномерная часть распределения поля;

n=1,2,3

Полученные значения (при n=1 и n=2) внесены в таблицу 2.3.1.

Как видно из таблицы 2.3.1, более точная аппроксимация распределения поля на раскрыве зеркала при n=2.

Выражение для нормированной диаграммы направленности антенны будет иметь вид:

(2.3.3)

где

n – показатель степени выражения, аппроксимирующего поле на раскрыве. (n=2)

Результаты расчета диаграммы направленности представим в виде таблицы 2.3.2

Таблица 2.3.2

, град	sin()		1(u)	31(u)	3(u)	3(u)
0 0.17 0.34 0.51 0.68 0.85 1.02 1.19 1.36 1.53 1.7	0 0.003 0.006 0.009 0.012 0.015 0.018 0.021 0.024 0.027 0.03	0 0.419 0.839 1.258 1.678 2.097 2.517 2.936 3.355 3.775 4.194	1 0.978 0.915 0.815 0.687 0.542 0.392 0.247 0.118 0.012 0.065	0.975 0.954 0.892 0.794 0.67 0.529 0.382 0.241 0.115 0.012 -0.064	1 0.985 0.93 0.9 0.837 0.81 0.74 0.627 0.498 0.392 0.316	0.675 0.665 0.628 0.608 0.565 0.547 0.5 0.423 0.336 0.265 0.213	1 0.981 0.921 0.85 0.748 0.652 0.535 0.402 0.273 0.168 0.09

Построим диаграмму направленности в декартовой системе координат

Рисунок 2.3.3 Диаграмма направленности антенны в декартовой системе координат