
- •Кафедра радиотехнических систем Курсовой проект по дисциплине «Теория электрических цепей» многоканальная система передачи информации
- •1.Задаваемые параметры и характеристики
- •2. Введение
- •3. Список условных обозначений и сокращений
- •4. Спи для телефонии
- •5. Спи для телеметрии
- •5.1. Выбор параметров корректирующего кода
- •5.2. Передающая часть
- •Групповой сигнал представлен на рисунке 5.1.
- •6. Выводы
- •7. Список использованной литературы
5. Спи для телеметрии
Дано:
10 телеметрических каналов
способ уплотнения временной
тип манипуляции в телеметрическом канале амплитудная
длина кодовой комбинации (пакета) в телеметрическом канале 7 бит
средняя скорость на входе телеметрического канала 4800 бит/с
корректирующий код, применяемый при передаче телеметрии РидаМюллера
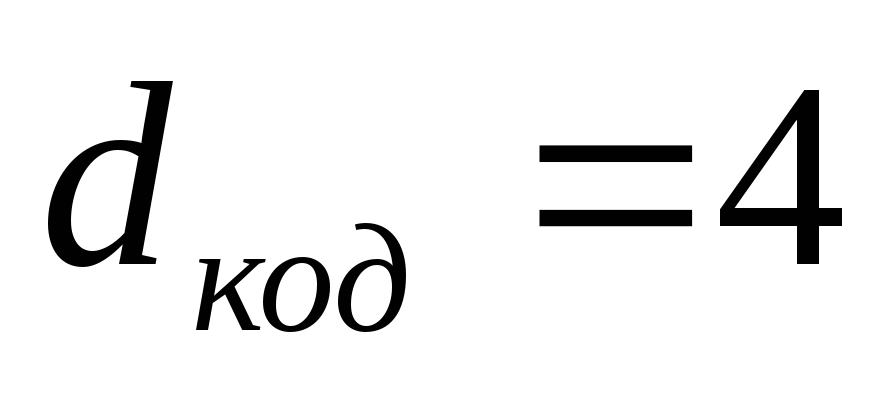
вероятность ошибки в одном символе в телеметрическом канале (ошибки независимы)
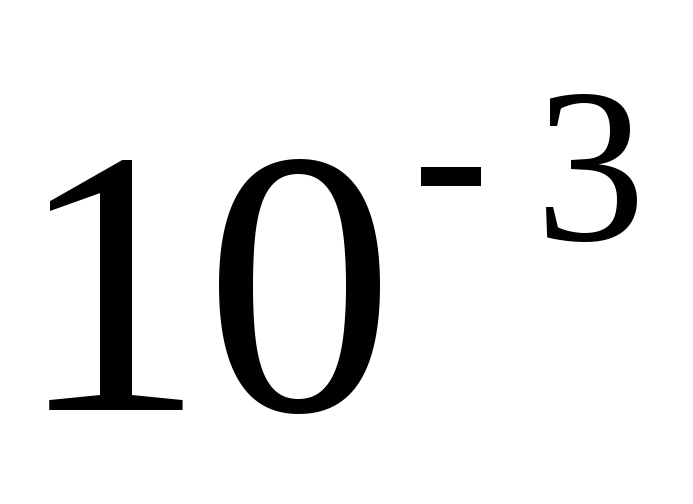
5.1. Выбор параметров корректирующего кода
Код РидаМюллера (РМ) относится к блочным кодам. Это означает, что цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга.
Код
РМ это разделимый
код, т.е. его
комбинации состоят из двух различающихся
частей: информационной и проверочной.
Информационные и проверочные разряды
во всех кодовых комбинациях всегда
занимают одни и те же позиции. Такие
коды обычно обозначают в виде (n,k),
где n
указывает значность кода (число позиций
в блоке), k
число информационных позиций. Таким
образом число проверочных символов в
разделимых кодах равно
![]() .
Код РМ этосистематический
(или линейный)
код. В таких кодах проверочные символы
образуются различными линейными
комбинациями информационных символов.
Теоретической основой получения таких
комбинаций является аппарат линейной
алгебры.
.
Код РМ этосистематический
(или линейный)
код. В таких кодах проверочные символы
образуются различными линейными
комбинациями информационных символов.
Теоретической основой получения таких
комбинаций является аппарат линейной
алгебры.
Код
РМ полностью определяется двумя
параметрами:
![]() и
и![]()
порядок кода. Число символов в кодовой
комбинации
порядок кода. Число символов в кодовой
комбинации
![]() ;
число информационных символов
;
число информационных символов![]() ,
где
,
где![]()
число сочетаний; кодовое расстояние
число сочетаний; кодовое расстояние
![]() .
У нас по заданию
.
У нас по заданию![]() ,
значит,
,
значит,![]()
Перечислим
коды РМ с
![]() :
:
(8,4) m=3, g=1, n=8, k=4, r=4
(16,11) m=4, g=2. N=16, k=11, r=5
(32,26) m=5, g=3. N=32, k=26, r=6
(64,57) m=6, g=4. N=64, k=57, r=7
(128,120) m=7, g=5. N=128, k=120, r=8
На практике часто используют укороченный код, когда r не изменяется, а kуменьшают. При этом неиспользуемые информационные символы заменяются нулями и не передаются.
Все коды с
![]() способны исправлять только однократные
ошибки, обнаруживать ошибки кратности
способны исправлять только однократные
ошибки, обнаруживать ошибки кратности![]() .
В системе передачи информации нет канала
переспроса, поэтому за вероятность
правильного (безошибочного) приема
примем вероятность того, что принятая
комбинация не содержит ошибок (содержит
ошибки кратности 0) или содержит ошибку
кратности 1 (используя корректирующую
способность кода можем исправить). Во
всех остальных случаях (когда кодовая
комбинация содержит ошибки кратностей
2;3;4;5;…) прием будет сопровождаться
ошибками.
.
В системе передачи информации нет канала
переспроса, поэтому за вероятность
правильного (безошибочного) приема
примем вероятность того, что принятая
комбинация не содержит ошибок (содержит
ошибки кратности 0) или содержит ошибку
кратности 1 (используя корректирующую
способность кода можем исправить). Во
всех остальных случаях (когда кодовая
комбинация содержит ошибки кратностей
2;3;4;5;…) прием будет сопровождаться
ошибками.
![]()
![]()
Для расчета вероятностей будем использовать биномиальную формулу (вероятность qкратной ошибки в кодовой комбинации длиной n):
![]() ,
гдервероятность
ошибки в одном символе.
,
гдервероятность
ошибки в одном символе.
Рассчитаем вероятности ошибочного приема при использовании различных кодов.
(78,70) из (128,120) при использовании укороченного кода
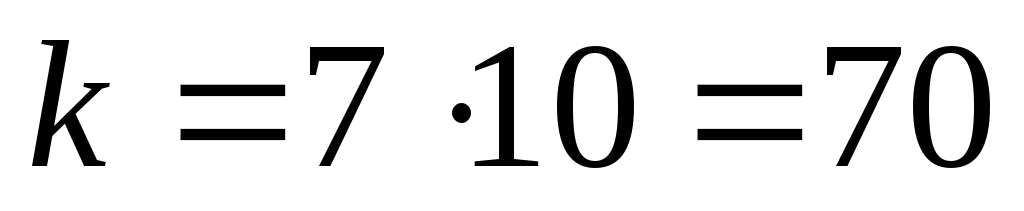 (выбираем
по одному пакету из каждого канала,
кодируем и передаем)
(выбираем
по одному пакету из каждого канала,
кодируем и передаем)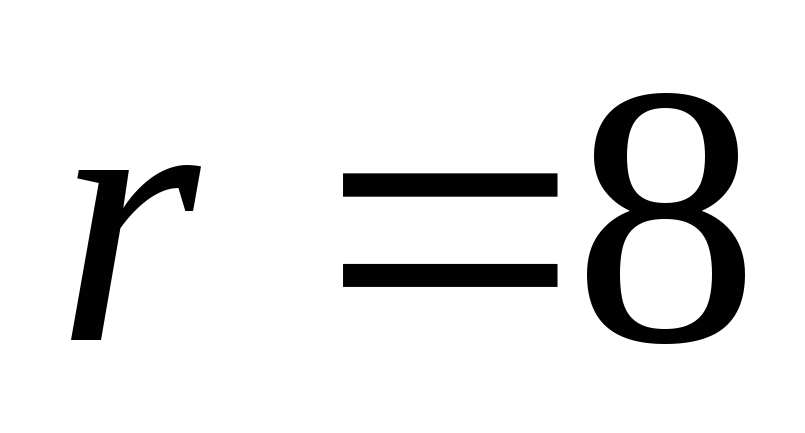
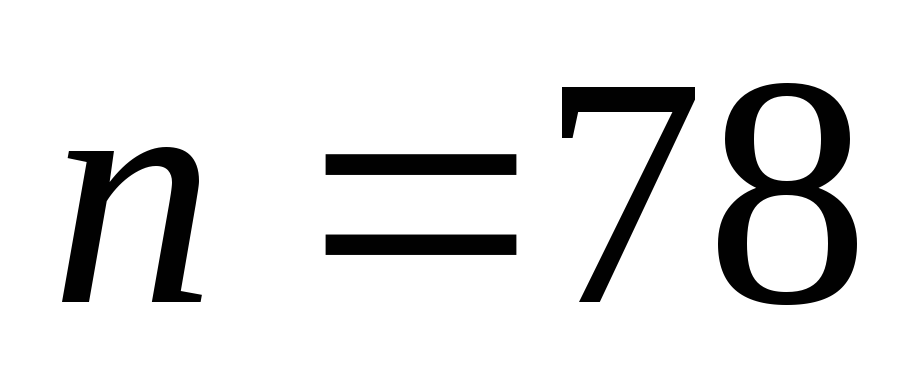
![]() .
.
В среднем приходится 1 ошибка на 350 символов;
средняя скорость возникновения ошибок 13,7 ош/сек;
среднее время между ситуациями, когда происходят ошибки73 мс.
(42,35) из (64,57) при использовании укороченного кода
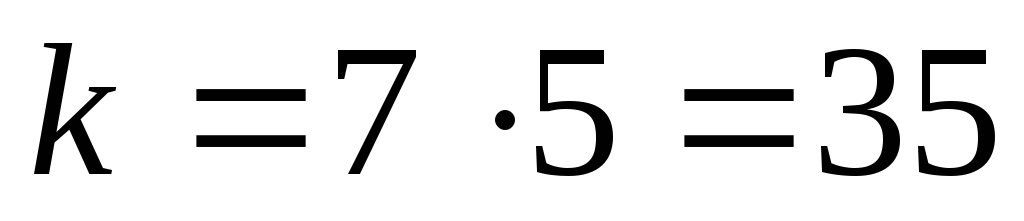 (выбираются
по одному пакету из пяти каналов,
кодируются и передаются)
(выбираются
по одному пакету из пяти каналов,
кодируются и передаются)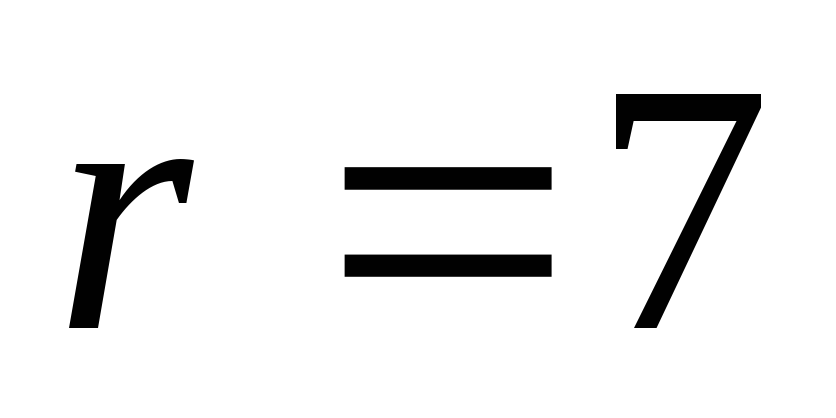

![]() .
.
В среднем приходится 1 ошибка на 1192 символа;
средняя скорость возникновения ошибок 4 ош/сек;
среднее время между ситуациями, когда происходят ошибки0,25 с.
(20,14) из (32,26) при использовании укороченного кода
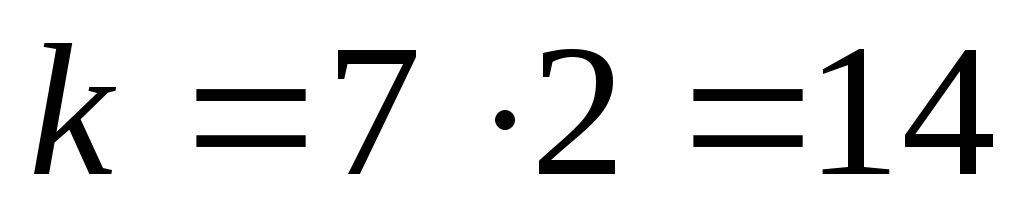 (выбираются
по одному пакету из каждого канала,
кодируются и передаются)
(выбираются
по одному пакету из каждого канала,
кодируются и передаются)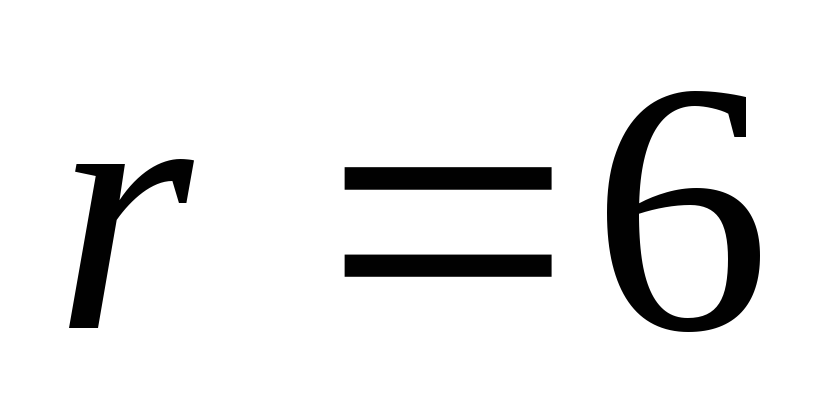
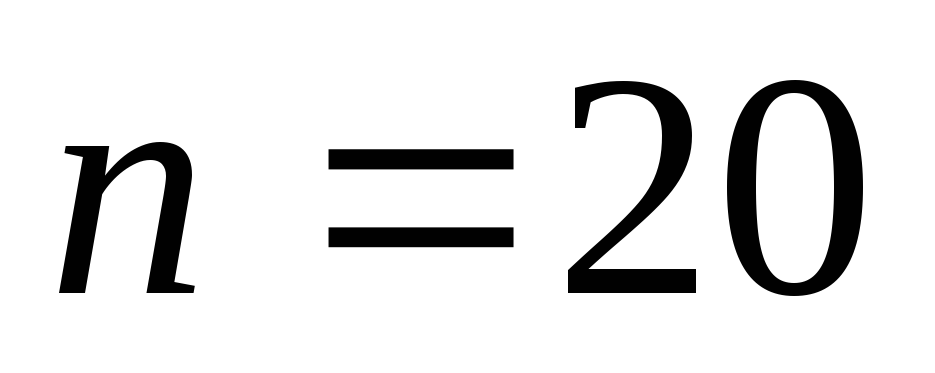
![]() .
.
В среднем приходится 1 ошибка на 5327 символов;
средняя скорость возникновения ошибок 0,9 ош/сек;
среднее время между ситуациями, когда происходят ошибки1,11с.
(12,7) из (16,11) при использовании укороченного кода
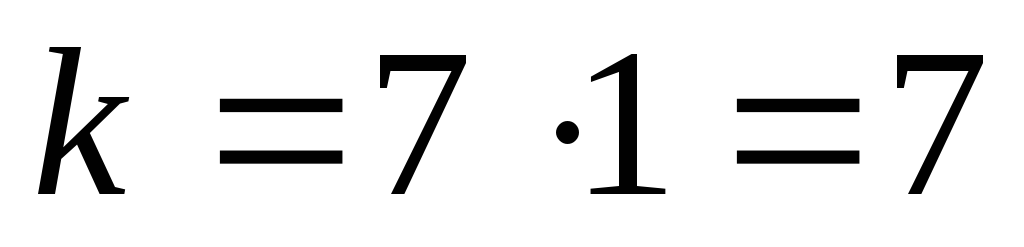 (выбираются
один пакет, кодируется и передаётся)
(выбираются
один пакет, кодируется и передаётся)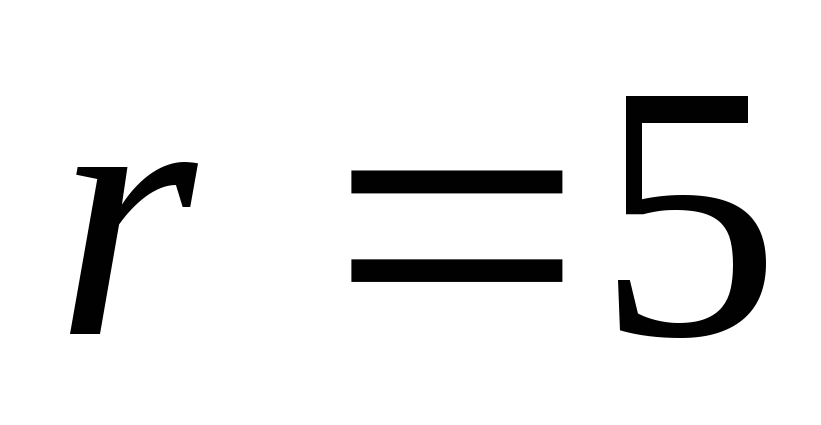
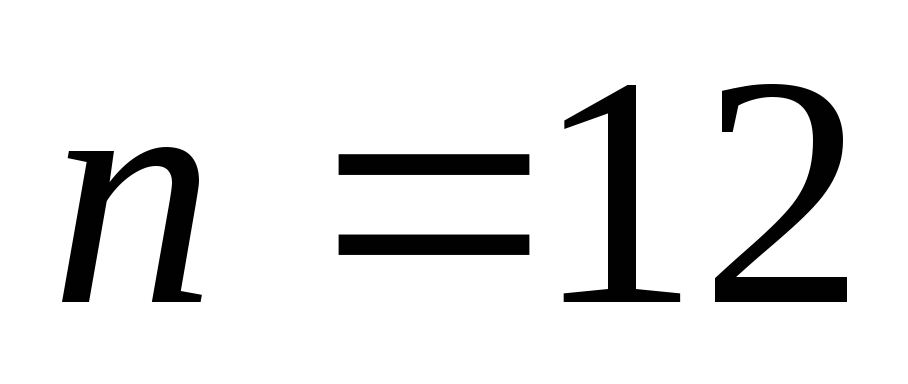
![]() .
.
В среднем приходится 1 ошибка на 15253 символа;
средняя скорость возникновения ошибок 0,3 ош/сек;
среднее время между ситуациями, когда происходят ошибки3,3 с.
(78,70) из (8,4) при использовании
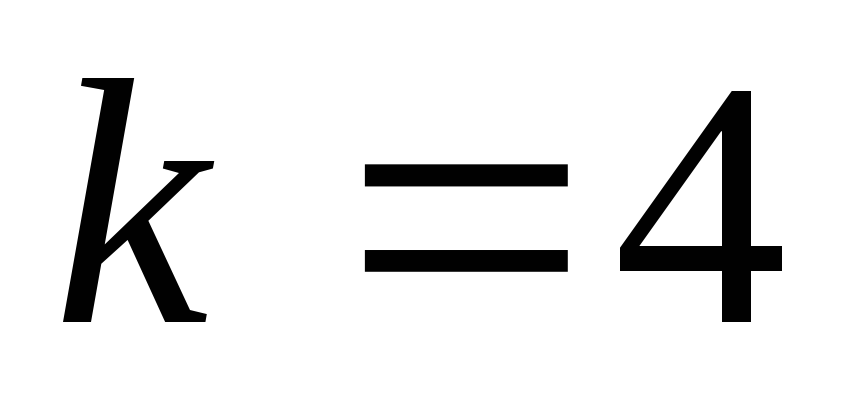 (выбираются
4 символа из пакета, кодируются и
передаются, берутся следующие 4 символа
снова передаются и т.д.)
(выбираются
4 символа из пакета, кодируются и
передаются, берутся следующие 4 символа
снова передаются и т.д.)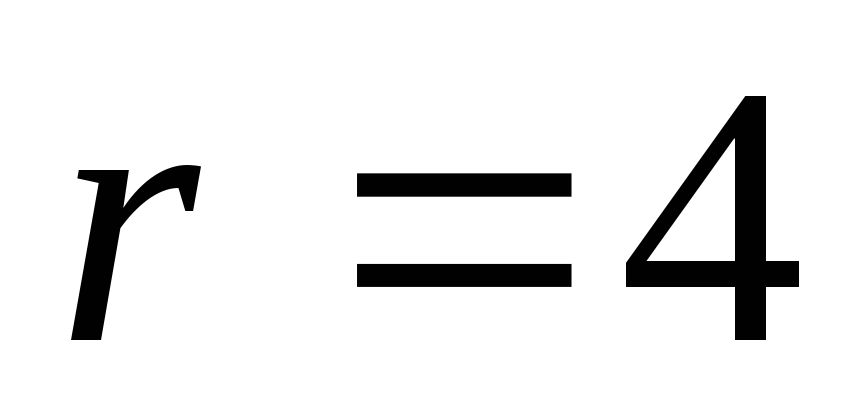

![]() .
.
В среднем приходится 1 ошибка на 35855 символов;
средняя скорость возникновения ошибок 0,13 ош/сек;
среднее время между ситуациями, когда происходят ошибки7,7 с.
При отсутствии корректирующего кода (пакеты каждого канала передаются напрямую)
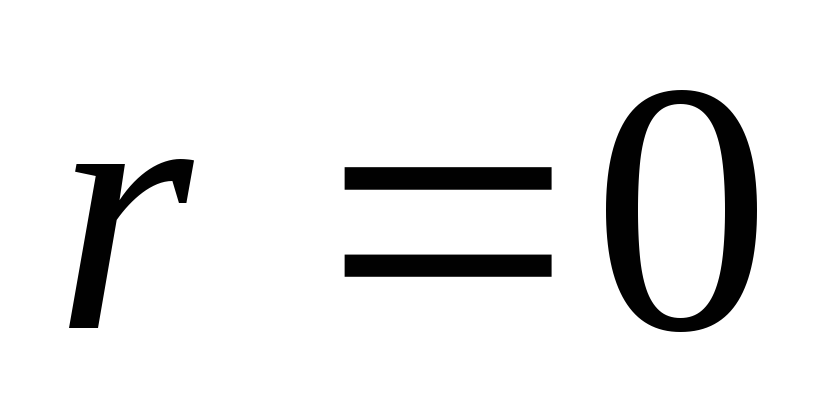
![]() .
.
В среднем приходится 1 ошибка на 143 символа;
средняя скорость возникновения ошибок 33,6 ош/сек;
среднее время между ситуациями, когда происходят ошибки30 мс.
В
качестве корректирующего кода разумно
выбрать укороченный код (12,7), получающийся
из кода (16,11). При этом избыточность
![]()
Заметим,
что код РидаМюллера
(16,11) по всем параметрам (![]() ,
кратности обнаруживаемых и исправляемых
ошибок) эквивалентен коду Хемминга
(15,11) с дополнительной общей проверкой
на четность, однако для кодов Хемминга
значительно легче получить проверочную
матрицу, которая необходима при
составлении схемы декодирующего
устройства. Поэтому в дальнейшем будем
использовать код (12,7) полученный из кода
Хемминга (15,11) с дополнительной проверкой
на четность.
,
кратности обнаруживаемых и исправляемых
ошибок) эквивалентен коду Хемминга
(15,11) с дополнительной общей проверкой
на четность, однако для кодов Хемминга
значительно легче получить проверочную
матрицу, которая необходима при
составлении схемы декодирующего
устройства. Поэтому в дальнейшем будем
использовать код (12,7) полученный из кода
Хемминга (15,11) с дополнительной проверкой
на четность.
Проверочная матрица имеет вид:

Примечание: если из этой матрицы вычеркнуть последнюю строку и последний столбец, то получится проверочная матрица для обычного кода Хемминга (15,11).
Производя перестановку столбцов эту матрицу не сложно привести к виду

Кодирование производится в два этапа:
1).
Формируется обычный код Хемминга
(используя матрицу без последней строки
и последнего столбца). Первые семь
символов (![]() )
объявляем информационными, следующие
4 символа (
)
объявляем информационными, следующие
4 символа (![]() )
не используются, т.к. код укороченный
(эти символы равны нулю), следующие 4
символа (
)
не используются, т.к. код укороченный
(эти символы равны нулю), следующие 4
символа (![]() )
проверочные для кода Хемминга.
)
проверочные для кода Хемминга.
![]() ;
;
![]()
![]()
![]()
2).
Формируется код Хемминга с общей
проверкой на четность. Для этого
формируется еще один проверочный символ
![]()
![]()
В
связи с тем, что символы
![]() не
используются, проверочную матрицу можно
привести (путем вычеркивания столбцов,
соответствующих
не
используются, проверочную матрицу можно
привести (путем вычеркивания столбцов,
соответствующих
![]() )
к виду
)
к виду

По
прежнему
![]()
информационные символы, а проверочные
информационные символы, а проверочные
![]()
![]() ;
;
![]()
![]()
![]()
![]()
Кодирование по прежнему производится в два этапа.
