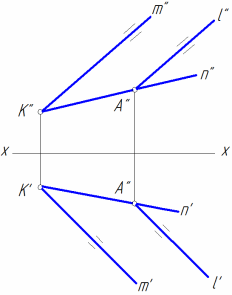
Взаимное положение прямой и плоскости
Прямая относительно плоскости может занимать различные положения: принадлежать плоскости, быть ей параллельной, пересекать плоскость.
Прямая принадлежит плоскости, если:
она проходит через две точки, принадлежащие данной плоскости (рис. 4, а);
она проходит через одну точку, принадлежащую данной плоскости, и параллельна прямой, находящейся в этой плоскости (рис. 4, б).
|
|
а |
б |
Рис. 4 |
|
Прямые особого положения в плоскости – линии уровня (горизонталь, фронталь) и линии наибольшего наклона к плоскостям проекции.
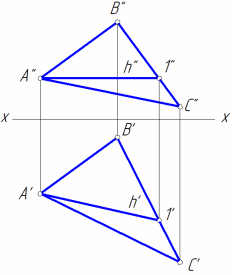
Горизонталями плоскости называются прямые, лежащие в ней и параллельные горизонтальной плоскости проекции (рис. 5, а).
Фронталями плоскости называются прямые, лежащие в ней и параллельные фронтальной плоскости проекции (рис. 5, б).
|
|
а |
б |
Рис. 5 |
|
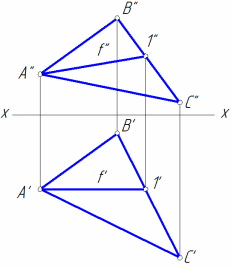
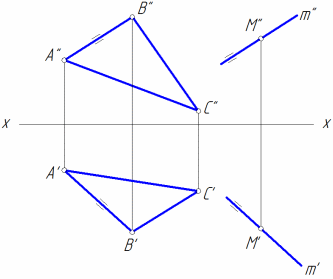
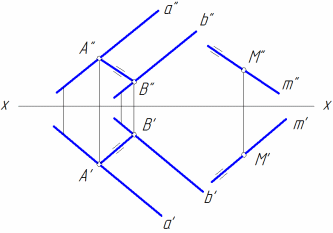
Прямая параллельна плоскости, если эта прямая параллельна любой прямой в плоскости. На рис. 6, а прямая m параллельна стороне треугольника АВ, на рис. 6, б прямая m параллельна отрезку АВ, построенному в плоскости, заданной двумя параллельными прямыми a и b.
|
|
а |
б |
Рис. 6 |
|
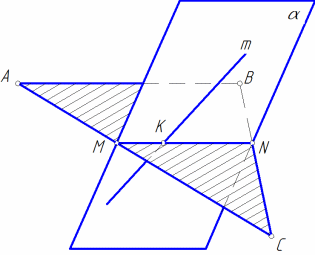
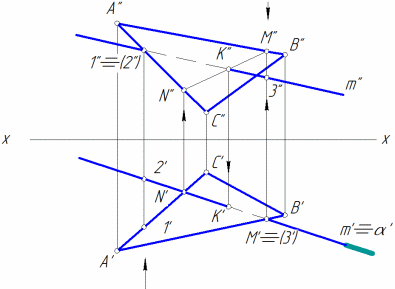
Прямая пересекает плоскость в точке, если она не параллельна этой плоскости (рис. 7, а). Для построения точки пересечения прямой m с плоскостью треугольника АВС необходимо выполнить следующие этапы:
через прямую m провести проецирующую плоскость ;
построить линию MN пересечения плоскости треугольника АВС и построенной плоскости ;
построить точку К пересечения заданной прямой m и построенной линии MN;
определить видимость прямой m относительно плоскости треугольника АВС (рис. 7, б).
|
|
а |
б |
Рис. 7 |
|
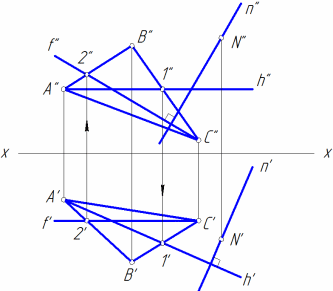
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым в этой плоскости (рис. 8, а). Для построения перпендикуляра n к плоскости , исходя из свойства проекций плоских углов, необходимо провести в заданной плоскости горизонталь и фронталь в качестве двух пересекающихся прямых (рис. 8, б).
|
|
а |
б |
Рис. 8 |
|
Определение натуральной величины отрезка общего положения
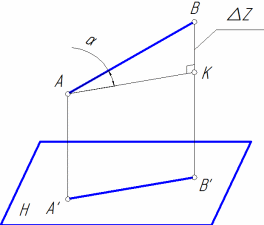
Отрезок общего положения проецируется на плоскости проекций с искажением. При этом ортогональная проекция отрезка всегда будет меньше его действительной величины (рис. 9, а).
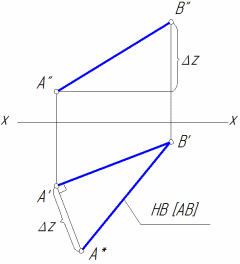
Для графического определения на эпюре натуральной величины (НВ) отрезка достаточно построить прямоугольный треугольник, взяв за один катет проекцию отрезка, а за другой катет – разность удаления концов отрезка от соответствующей плоскости проекции (рис. 9, б).
|
|
а |
б |
Рис. 9 |
|
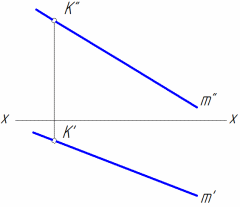
Если необходимо на прямой общего положения m (рис. 10, а) от заданной точки К отложить отрезок определенной длины требуется выполнить следующие построения:
на прямой m задать произвольную точку M;
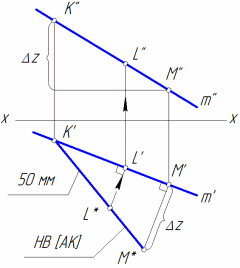
найти НВ отрезка КМ;
отложить на полученной НВ отрезок заданной длины и построить его проекции (рис. 10, б).
|
|
а |
б |
Рис. 10 |
|
