Модуль 2

Лекция 14. Производная

14.1.Понятие производной. Геометрический смысл производной

14.2.Дифференцируемость функции. Критерий дифференцируемости

14.3.Дифференциал. Геометрический смысл дифференциала. Связь дифференциала функции с производной

14.4.Свойства производных

14.5. Производные основных элементарных функций

14.6. Понятие локального экстремума. Точки перегиба

14.7. Выпуклость и вогнутость функции

14.8. Применение производных к исследованию функций

14.9.Правила Лопиталя для раскрытия неопределенностей

Программные положения

Исторически рассмотрение задач о касательной и скорости движения привело к понятию производной, являющемся одним из основных понятий высшей математики. При решении этих задач приходится выполнять одну и ту же операцию – находить предел отношения приращения функции к приращению аргумента. Производные первого и второго порядка помогают характеризовать поведение функции (возрастание-убывание, выпуклость-вогнутость графика, находить точки экстремума и др.)

Методические рекомендации

Обратите внимание, что необходимые условия существования в точке экстремума или перегиба не являются достаточными

Литература

А.В.Дорофева «Высшая математика» лава 8 «Производная» (стр. 178-203)

Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава IX «Производная» (стр. 144-155), глава Х «Основные теоремы о производных» (стр.155-182),

Глава XI «Приложения производной» (стр.182-214), глава XII «Дифференциал» (стр214-228)

А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков Математика для психологов» Часть II «Математический анализ» Глава 1 «Исходные идеи дифференциального исчисления»(стр. 130-148) , глава 2 «Предел и производная» (148-159), глава 5 «Производные и неопределенные интегралы» глава 6 «Производные от некоторых функций» (стр.180-192)

Дополнительно

А.Я.Хинчин «8 лекций по математическому анализу» Лекция V (стр.120-156)

Р.Курант, Г.Роббинс «Что такое математика?» глава VIII «Математический анализ» §1-3 (стр. 442-461), Дополнение к главе VIII §1 п.1 «Дифференцируемость» стр.491-493

Контрольные вопросы

1. Дайте определение производной функции

2. Каков геометрический смысл производной

3. Что такое дифференциал функции? Каков его геометрический смысл?

4.Найти производные следующих функций:

1)	;	2)	;
3)	;	3)	;
5)	;	6)	;
7)	;	8)	;
9)	;	10)	;
11)	где x = 1;	12)	;
13)	где t =  / 6;	14)
15)	;	16)	.

5. Разберите вывод формул производных основных элементарных функций

6. По правилу Лопиталя найти пределы

7. Обоснуйте первое и второе утверждения о достаточном условии перегиба (п.14.6)

8. Докажите теорему 14.7

9. Исследуйте поведение функций и постройте графики

14.1.Понятие производной. Геометрический смысл производной

Исторически рассмотрение задач о касательной и скорости движения привело к понятию производной, являющемся одним из основных понятий высшей математики. При решении этих задач приходится выполнять одну и ту же операцию – находить предел отношения приращения функции к приращению аргумента. Рассмотрим эти задачи.

Рассмотрим функцию y=f(x), непрерывную в некоторой окрестности точки x. Пусть  x приращение аргумента в точке x. Обозначим через y или f приращение функции, равное f(x+x) – f(x). Отметим здесь, что функция непрерывна в точке x, если в этой точке бесконечно малому прира­щению аргу­мента x соответствует беско­нечно малое приращение функции f.

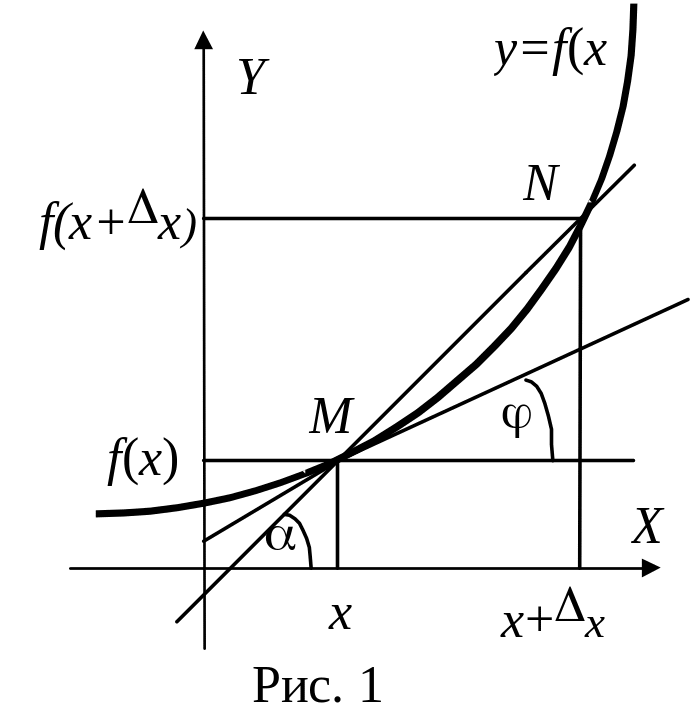
Отношение f /x, как видно из рисунка 1, равно тангенсу угла , который составляет секущая MN кривой y = f(x) c положительным направлением горизонтальной оси координат.

Представим себе процесс, в котором величина x, неограниченно уменьшаясь, стремится к нулю. При этом точка N будет двигаться вдоль кривой y = f(x), приближаясь к точке M, а секущая MN будет вращаться около точки M так, что при очень малых величинах x её угол наклона  будет сколь угодно близок к углу  наклона касательной к кривой в точке x.

Определение 14.1.(1)

Касательной к данной непрерывной кривой в данной ее точке М (точка касания) называется предельное положение секущей MN, проходящей через точку М, когда вторая точка пересечения N неограниченно приближается по кривой к первой.

Если секущая MN при M→N не имеет предельного положения, то говорят, что касательной к данной линии в точке М не существует.

Следует отметить, что все сказанное относится к случаю, когда график функции y = f(x) не имеет излома или разрыва в точке x, то есть в этой точке можно провести касательную к графику функции.

Определение 14.1.(2)

Отношение y / x или, что то же самое (f(x + x)  f(x)) / x, можно рассматривать при заданном x как функцию аргумента x. Эта функция не определена в точке x = 0. Однако её предел в этой точке может существовать.

Если существует предел отношения (f(x + x) – f(x)) / x в точке x = 0, то он называется производной функции y = f(x) в точке x и обозначается y или f(x):

.

Определение 14.1.(3).

Нахождение производной функции y = f(x) называется дифференцированием.

Если для любого числа x из открытого промежутка (a, b) можно вычислить f(x), то функция f(x) называется дифференцируемой на промежутке (a, b) (см. 14.2).

Геометрический смысл производной заключается в том, что произ­водная функции f(x) в точке x равна тангенсу угла наклона касательной к графику функции в этой точке.

То есть, угловой коэффициент касательной к графику функции равен значению ее производной в точке касания, т.е. k = f ´(x). Зная угловой коэффициент касательной, легко написать ее уравнение. Касательная MN проходит через точку касания M(x₀,y₀), поэтому ее уравнение имеет вид y - y₀ = k(x - x₀) , где x, y - текущие координаты. Подставляя сюда значение углового коэффициента k и учитывая, что M лежит на линии, получаем уравнение касательной y – f(x₀) = f ´(x₀) (x - x₀)

Производная - это скорость изменения функции в точке x. Из определения производной следует, что f (x)  f / x, причем точность этого приближенного равенства тем выше, чем меньше x. Производная f (x) является приближенным коэффициентом пропорциональности между f и x.

Производная функции f(x) не существует в тех точках, в которых функция не является непрерывной. В то же время функция может быть непрерывной в точке x₀, но не иметь в этой точке производной. Такую точку назовём угловой точкой графика функции или точкой излома. Графические примеры приведены на рисунке 2.

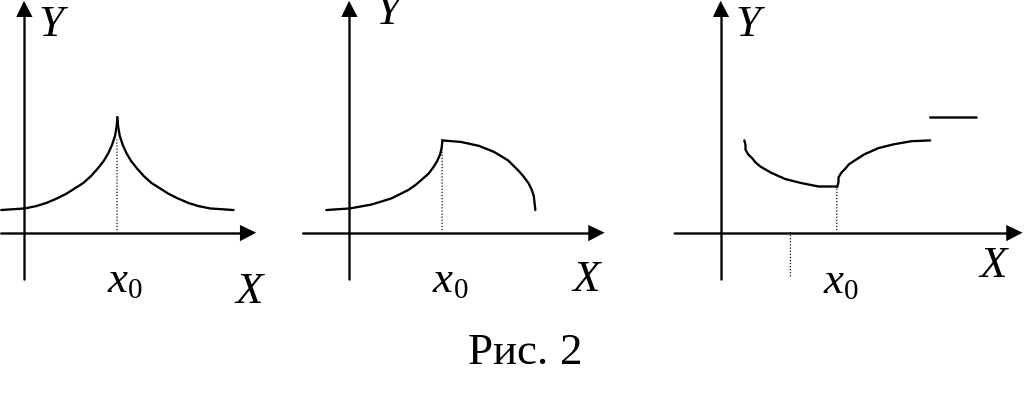
Так функция y = x  не имеет производной в точке x = 0, хотя является непрерывной в этой точке.

Замечание 14.1.

Для обозначения производной данной функции y = f(x) употребляются символы:

Точка над знаком функции используется также для обозначения дифференцирования по переменной t, время

В тех случаях, когда неясно, по какому аргументу происходит дифференцирование функции y = f(x) для обозначения производной используются обозначения :

Пример 14.1.

Найдем производную функции y = x² .

Пусть х -произвольное фиксированное значение аргумента. Давая х приращение Δх≠0, будем иметь y + Δy = (x +Δx)² . Отсюда

и, следовательно,

.

Таким образом, (х² )́ = 2х

Определение 14.1(4)

Может оказаться, что функция f(x), называемая первой производной, тоже имеет производную (f(x)). Эта производная называется второй производной функции f(x) и обозначается f(x). Если f есть координата движущейся точки и является функцией времени, то мгновенная скорость точки в момент времени t равна f(t), а ускорение равно f(t).

Вторая производная также может быть функцией, определенной на некотором множестве. Если эта функция имеет производную, то эта производная называется третьей производной функции f(x) и обозначается f(x).

Если определена n-я производная f ⁽ⁿ⁾(x) и существует её произ­водная, то она называется (n+1)-й производной функции f(x): f ^(n + 1)(x) = (f⁽ⁿ⁾(x)).

Все производные, начиная со второй, называются производными высших порядков.

Для обозначения производных порядка выше третьего вместо нескольких штрихов производной используют (n) для производной порядка n.

Пример 14.1 (2).

Найти