1. Статический момент площади. Центр тяжести сечения.

Статический момент относительно некоторой оси – это взятая по всей площади F сумма произведений элементарных площадок dF на расстояние до этой оси.

	(2)
	(3)

Рассмотрим произвольное сечение площадью F. Выделим элементарную площадку dF с координатами x и y в данной системе координат XY. Параллельно осям XY введем новую систему координат X₁Y₁ на расстоянии a и b между осями.

Рисунок 3.2 – Определение координат центра тяжести сечения

(4)

По аналогии с формулами (2) и (3) можно записать:

(5)

(6)

Центральными называются оси, относительно которых статические моменты равны 0. Точку пересечения центральных осей называют центром тяжести сечения.

Пусть оси X₁Y₁ – центральные, следовательно, уравнения (5) и (6) имеют вид:

0 = S_x – aF;

0 = S_y – bF;

Выполним подстановку: а = y_c, b = x_с, следовательно:

где, x_c и y_c – координаты центра тяжести относительно произвольной системы координат XY.

Если сечение сложное, то (7) запишется:

;

Здесь знак ∑ - алгебраический.

Статический момент конечной площади равен произведению величины этой площади на расстояние от ее центра тяжести до оси, относительно которой берется статический момент.

Рисунок 3.3 - Пример

F₁ = F₂ = 4a²

x₁ = 2a; x₂ = 2a

Если сечения имеет ось симметрии, то эта ось – центральная.

y₁ = 3a, y₂ = = 0,5a

2. Осевые, полярные, центробежные моменты инерции сечения.

Осевым моментом инерции относительно некоторой оси называют взятую по всей площади F сумму произведений элементарных площадок dF на квадрат расстояния до этой оси.

Полярным моментом инерции относительно некоторого полюса называется взятая по всей площади F сумма произведений элементарных площадок dF на квадрат расстояния до этого полюса:

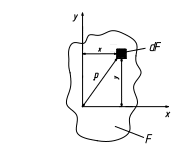
Рисунок 3.4 - Пример

Полярный момент инерции равен сумме осевых моментов инерции.

Рассмотрим как пользоваться интегралом (9) для определения момента инерции для прямоугольного поперечного сечения. Выделим элементарную площадку высотой dy на расстоянии у от оси х. Площадь этой площадки определяется:

Рисунок 3.5 – Прямоугольное сечение

Значение для простых фигур приведены в справочной литературе. Для наиболее распространенных сечений эти значения приведены в таблице 3.1

Таблица 3.1 – Моменты инерции

№	Сечение	Ix	Iy	№	Сечение	Ix	Iy
1				2
3				4
5				6		0,11xR4

Примечание к таблице:

1. Оси Х и У – центральные оси

2. Для второй и пятой фигур значения I_x и I_y не изменяются при любом повороте оси.

3. Для первой, третьей, четвертой фигур в кубе берется та сторона, которую пересекает данная ось.

Центробежным моментом инерции относительно двух взаимно перпендикулярных осей называется сумма произведений элементарных площадок dF на расстояния до этих осей

Момент сопротивления сечения определяется из выражения:

,

y_max – это расстояние от оси Х до наиболее удаленной точки сечения.

X_max – расстояние от оси у до наиболее удаленной точки сечения.

Продолжим рассмотрение примера пункта 3.1