4. Основные гипотезы науки о сопротивлении материалов.

Для построения теории сопротивления материалов принимают некоторые гипотезы относительно структуры и свойств материалов, а также о характере деформации. Эти гипотезы следующие:

1. Гипотеза о сплошности материала. Предполагается, что материал сплошь заполняет форму тела. Атомистическая теория дискретного строения вещества во внимание не принимается.

2. Гипотеза об однородности и изотропности. Материал предполагается однородным и изотропным, т.е. в любом объеме и в любом направлении свойства материала считаются одинаковыми. Хотя кристаллы, из которых состоят металлы анизотропны, но их хаотическое расположение дает возможность считать макрообъемы металлов изотропными.

В некоторых случая предположение об изотропии неприемлемо. Например к анизотропным материалам относятся древесина, свойство которой вдоль и поперек волокон существенно различны, армированные материалы и т.п.

3. Гипотеза о малости деформаций. Предполагается, что деформации малы по сравнению с размерами тела. Это позволяет в большинстве случаев пренебречь изменениями в расположении внешних сил относительно отдельных частей тела и составлять уравнения статики для недеформированного тела. В некоторых случаях от этого принципа приходится отступать. Такие отступления оговариваются особо. Малые относительные деформации рассматривают как бесконечно малые величины.

4. Гипотеза об идеальной упругости материала. Все тела предполагаются особо упругими. Отклонения от идеальной упругости, которые всегда наблюдаются при нагружении реальных тел, не существенны и ими пренебрегают до определенных пределов деформирования.

Большинство задач сопротивления материалов решают в предположении линейно – деформируемого тела, т.е. такого, при котором справедлив закон Гука, выражающий прямую пропорциональность между деформациями и нагрузками.

Приняв о малости деформации и по линейной зависимости между деформациями и усилиями, можно при решении большинства задач сопротивления материалов применять принцип суперпозиции (принцип независимости и сложения действия сил). Например, усилия в любом элементе конструкции, вызванные различными факторами (несколькими силами, температурными воздействиями), равны сумме усилий, вызванных каждым из этих факторов, и не зависят от порядка их приложения. Это же справедливо и в отношении деформации.

Перечисленные выше гипотезы, а также некоторые другие, о которых будет сказано дальше, позволяют решать широкий круг задач по расчету на прочность, жесткость и устойчивость. Результаты расчетов хорошо согласуются с данными практики.

5. Внешние силы взаимодействия между телами

Внешние силы делятся на:

1. сосредоточенные силы – когда площадь приложения силы несоизмеримо мала по сравнению с размерами тела (рисунок 1.8)

Рисунок 1.8 – Сосредоточенное усилие

2. распределенная нагрузка – площадь приложения которой соизмерима с размерами тела (рисунок 1.9)

Рисунок 1.9 – Распределенная нагрузка

Распределенные силы могут непрерывно распределены по всей поверхности тела или ее части; например: давление паров в котле, ветровая и снеговая нагрузки, давление газов в цилиндре двигателя. Величина нагрузки, приходящаяся на единицу площади, называется интенсивностью нагрузки. Интенсивностью такой нагрузки (Н/м, кН/м, МН/м) называют величину нагрузки, приходящуюся на единицу длины линии. Интенсивность может быть переменной по этой длине.

В случае равномерно распределенной нагрузки (рисунок 1.9) эпюра q прямоугольная.

Отметим, что равнодействующая распределенной нагрузки численно равна площади ее эпюры и приложена в центре ее тяжести. Q = ql

3. пара сил или сосредоточенный изгибающий момент (рисунок 1.10)

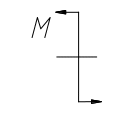
Рисунок 1.10 – Пара сил

В зависимости от характера приложения сил во времени различают нагрузки статические и динамические. Нагрузка считается статической, если она сравнительно медленно и плавно (хотя бы в течение нескольких секунд) возрастает от нуля до своего конечного значения, а затем остается неизменной. При этом можно пренебречь ускорениями деформируемых масс, а значит и силами инерции.

Динамические нагрузки сопровождаются значительными ускорениями как деформированного тела, так и взаимодействующих с ним тел. При этом возникают силы инерции, которыми нельзя пренебречь. Динамические нагрузки делят на мгновенно приложенные, ударные и повторно – переменные.

Нагрузка считается мгновенно приложенной, если она возрастает от нуля до своего конечного значения в течение очень короткого промежутка времени (доли секунды). Такова нагрузка при воспламенении горючей смеси в цилиндре двигателя внутреннего сгорания или при трогании с места железнодорожного состава.

Для ударной нагрузки характерно то, что в момент ее приложения тело, вызывающее нагрузку, обладает определенной кинетической энергией. Такая нагрузка получается, например, при забивании свай с помощью копра, в деталях механического кузнечного молота и т.д.

Многие детали машин (шатуны, валы, оси железнодорожных вагонов и пр.) подвержены действию нагрузок, непрерывно и периодические меняющихся во времени. Такие нагрузки называют повторно – переменными. Они, как правило, сопряжены с циклически повторяющимися движениями детали. Это возвратно – поступательное движение штока поршня, колебания элементов конструкции и др.

Внутренние силы. Метод сечений.

Между соседними частицами тела (кристаллами, молекулами, атомами) всегда имеются определенные силы взаимодействия, иначе – внутренние силы. Эти силы во всех случаях стремятся сохранить его как единое целое, противодействуют всякой попытке изменить взаимное расположение частиц, т.е. деформировать тело. Внешние силы, наоборот, всегда стремятся вызвать деформацию тела, изменить взаимное расположение частиц. Следовательно, величина внутренних сил, действующих между двумя какими – либо частицами, в нагруженном и ненагруженном теле будет различна.

В сопротивлении материалов не рассматривают и не принимают во внимание внутренние силы, действующие в теле, которое находится в своем естественном (ненагруженном) состоянии, а изучают и вычислят только те дополнительные величины внутренних сил, которые появляются в результате нагружения тела. Поэтому в дальнейшем, говоря о внутренних силах, будем иметь ввиду именно эти дополнительные силы взаимодействия, возникающие в результате нагружения. Внутренние силы часто называют усилиями.

Для выявления, а затем и вычисления внутренних сил в сопротивлении материалов широко применяют метод сечений.

Рассмотрим произвольное тело, нагруженное самоуравновешенной системой сил. В интересующем нас месте мысленно рассечем его некоторой плоскостью I-I на две части – 1 и 2 (рисунок 1.11а). При этом само сечение будет иметь две стороны: одну, принадлежащую части 1 тела (левую), и вторую, принадлежащую части 2 (правую). В каждой точке обеих сторон сечения будут действовать силы взаимодействия. Исходя из введенной гипотезы о сплошности материала следует считать, что внутренние силы действуют во всех точках приведенного сечения и, следовательно представляют собой распределенную нагрузку. В зависимости от формы тела и характера внешних нагрузок интенсивность внутренних сил в различных точках может быть различна.

Следует подчеркнуть что внешние силы, действующие по сечению, принадлежащему части 1 тела, в соответствии с третьим законом Ньютона равны по величине и противоположны по направлению внутренним силам, действующим по сечению, принадлежащему части 2 тела. Другими словами, внутренние силы, действующие на различные части, взаимны. Как всякую систему сил, их можно привести к одной точке, в результате чего на каждой стороне сечения получим главный вектор и главный момент внутренних сил в сечении (рисунок 1.11б).

Стержень, в частности, рассекают обычно плоскостью, перпендикулярной к оси, т.е. поперечным сечением. Если главный вектор и главный момент внутренних сил спроецировать на ось стержня z и главные центральные оси сечения у и х, то на каждой стороне сечения получим 6 внутренних силовых факторов (рисунок 1.12): три силы (N, Q_y, Q_x), и три момента (M_x, M_y, M_z). Эти величины называют внутренними усилиями в сечении стержня.

а) б)

Рисунок 1.11 – Метод сечений

- главный вектор сил

- главный момент

Рисунок 1.12 – Внутренние силы

N – продольная сила, вызывающая растяжение или сжатие

Q_y, Q_x - поперечная сила, вызывающая изгиб

M_x, M_y – изгибающий момент

M_кр – крутящий момент

Рисунок 1.13 - Пример

∑y = 0 -P-N₂ sin α = 0 => N₂ = -

∑x = 0 -N₁-N₂ cos α => N₁ = P ctg α