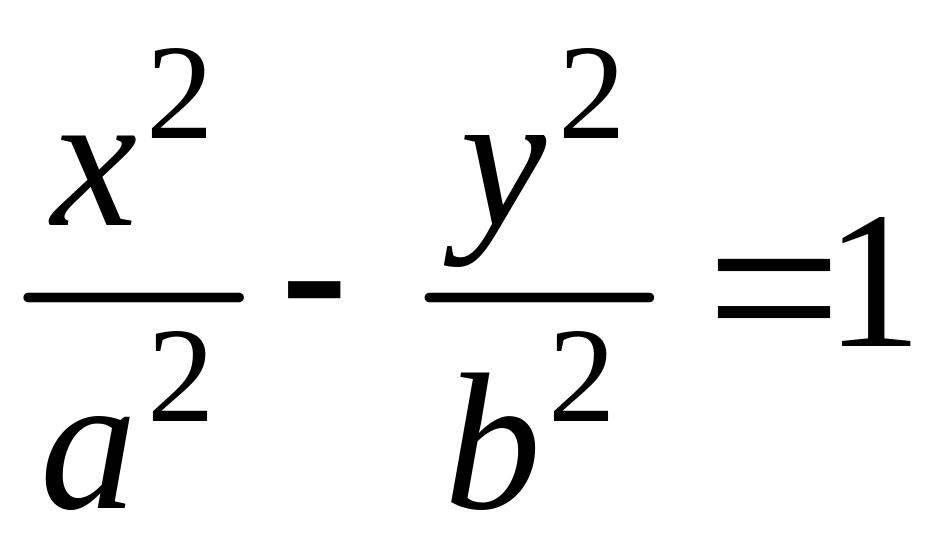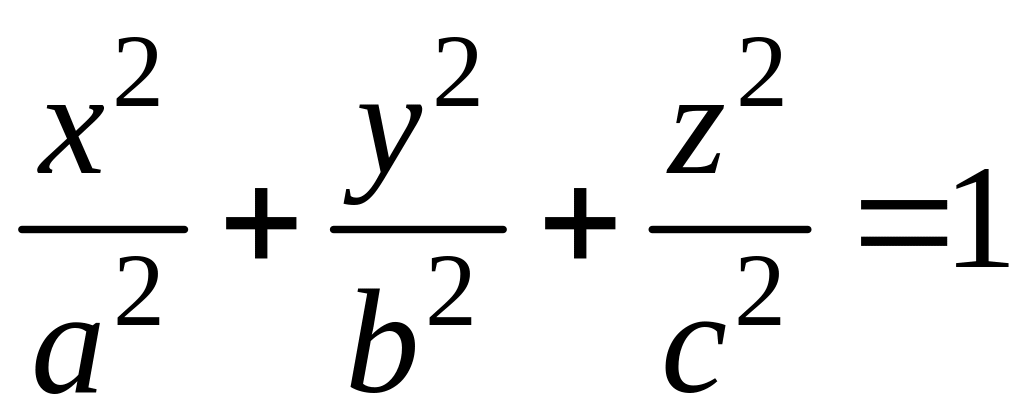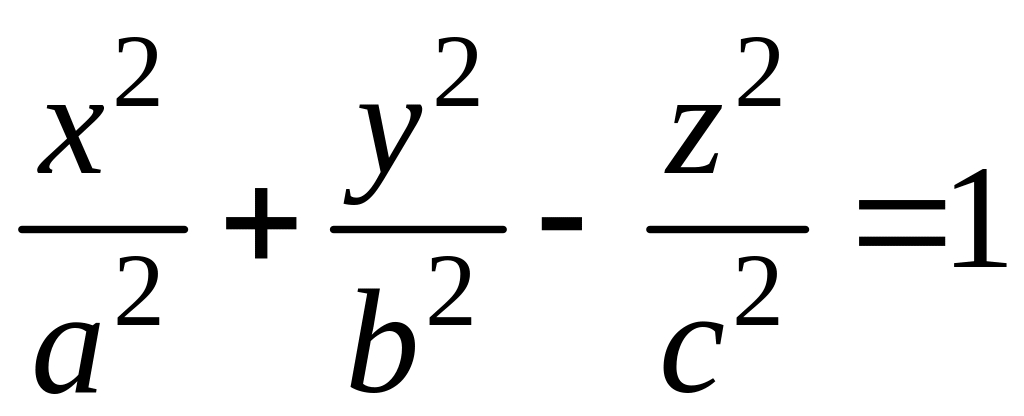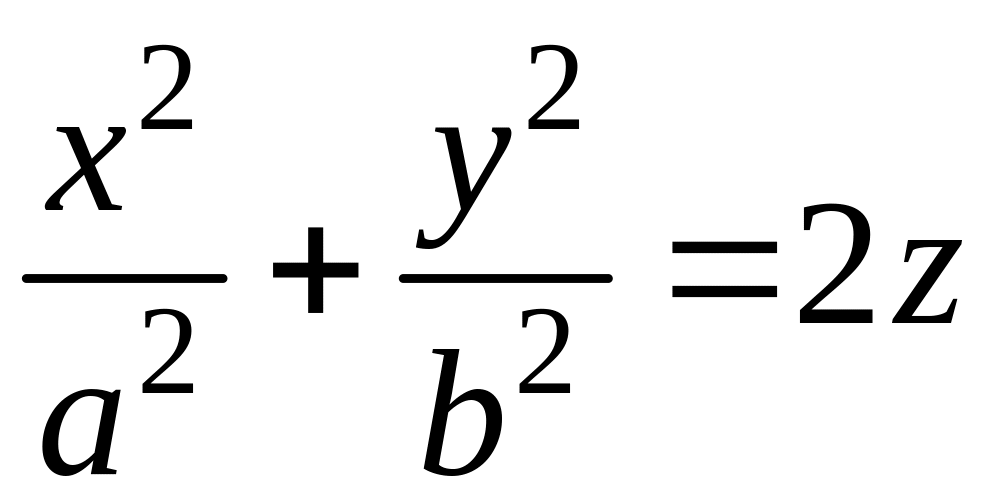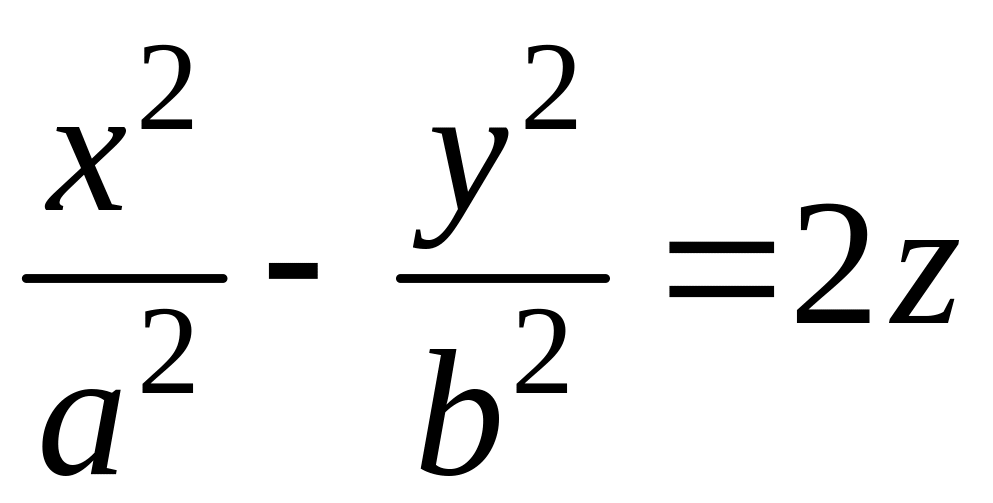3. 2. Взаимное расположение прямых на плоскости

Пусть даны две прямые, заданные общими или каноническими уравнениями, уравнениями с угловыми коэффициентами.

Углом  между прямыми называется наименьший из двух смежных углов, образованных этими прямыми.

Для прямых, заданных уравнениями с угловыми коэффициентами, тангенс угла между прямыми находится по формуле:

.

Если прямые заданы общими или каноническими уравнениями, то задача об определении угла между прямыми сводится к определению угла между нормальными или направляющими векторами:

Рассмотрим условия параллельности и перпендикулярности прямых.

Если прямые заданы уравнениями с угловыми коэффициентами:

l₁: y=k₁x+b, l₂: y=k₂x+b, то

l₁  l₂  k₁=k₂

l₁  l₂  k₁k₂=-1 или .

Если прямые заданы общими уравнениями:

l₁: A₁x+B₁y+C=0, l₂: A₂x+B₂y+C=0, то

l₁  l₂   

l₁  l₂     =0  A₁B₁+A₂B₂=0.

Если прямые заданы каноническими уравнениями:

l₁: , l₂: , то

l₁  l₂   

l₁  l₂     =0  m₁n₁+m₂n₂=0.

4. Кривые второго порядка

Уравнения кривых второго порядка представлены в табл. 2.

Таблица 2

Тип уравнения	Формула
Уравнение окружности с центром (, ) и радиусом R
Уравнение эллипса с центром (, ) и полуосями a и b
Уравнения гиперболы с центром (, ) и полуосями a и b
Уравнение параболы с центром (, ) и ветвями, направленными вдоль оси: Ох Оу	2p(x – ) =(y – )2 2p(y – )=(x – )2

5. Поверхности второго порядка

5. 1 . Основные типы поверхностей

Классификация поверхностей в пространстве находится в полной аналогии с классификацией линий на плоскости.

Определение. Поверхность второго порядка – это множество точек трехмерного пространства, координаты которых в декартовой системе координат удовлетворяет уравнению (описывается в общем случае многочленом второго порядка):

Ax²+By²+Cz²+Dxy+Еxz+Fyz+Gx+Hy+Kz+L=0,

в котором A²+B²+C²+D²+Е²+F²  0.

Таблица 3

Тип поверхности		Уравнение		Чертеж
Эллиптический цилиндр
Гиперболический цилиндр				a b y x z 0
Параболический цилиндр
Эллипсоид
Однополостный гиперболоид
Двуполос- тный гиперболоид				x 0
Эллиптический параболоид

Гиперболический параболоид
Конус	z2=x2+y2