Министерство образования и науки Российской Федерации

Сибирский федеральный университет

аналитическая

геометрия

Практикум

Красноярск

СФУ

2012

УДК 514.12(07)

ББК 22.151.54я73

Составители: М. Н. Арасланова, Т. П. Мансурова

Аналитическая геометрия: практикум [Текст] / сост. М. Н. Арасланова, Т. П. Мансурова. – Красноярск: Сиб. Федер. Ун-т, 2012. – 64 с.

В практикуме приведены основные теоретические сведения раздела математики «Аналитическая геометрия» и разобраны примеры решения типовых задач.

Предназначено для студентов всех специальностей направлений: 130100 Прикладная геология, 130200 Технологии геологической разведки, 130400 Горное дело, 140600 Электротехника, электромеханика и электротехнологии, 150400 технологические машины и оборудование, 150000 Металлургия, машиностроение и металлообработка, 280100 Безопасность жизнедеятельности, 150700 Физическое материаловедение, 080500 Менеджмент.

УДК 514.12(07)

ББК 22.151.54я73

Сибирский

федеральный

университет, 2012

Введение

Значение раздела «аналитическая геометрия» математики определяется тем, что подавляющее большинство прикладных задач носят “линейный” характер, а те, что не являются “линейными”, как правило, допускают “линеаризацию”.

Сплав двух важнейших идей - идеи координат и идеи вектора - и лежит в основе учебной дисциплины “линейная алгебра с элементами аналитической геометрии”. Математический аппарат, которым студент овладевает в процессе ее изучения, используется практически во всех приложениях математики.

Практикум написан в соответствии с программой данного курса. Содержит элементы аналитической геометрии, теорию определителей, систем линейных уравнений, векторов. Отличается большим количеством типовых примеров.

1. Уравнение плоскости

1.1. Различные виды уравнений плоскости

Уравнение называется общим уравнением плоскости.

Здесь – нормальный вектор плоскости (вектор, перпендикулярный плоскости (рис. 1)).

Рис. 1

Общее уравнение плоскости называется полным, если все его коэффициенты не равны нулю, в противном случае оно называется неполным.

Рассмотрим различные виды неполных уравнений:

1. D = 0  OP;

2. A = 0  P || Ox; B = 0  P || Oy; C = 0  P || Oz;

3. A = B = 0  P  Oz; A = C = 0  P  Oy; B = C = 0  P  Ox;

4. D = A = 0  Ox  P; D = B = 0  Oy  P; D = C = 0  Oz  P;

5. D = A = B  P  xOy; D = A = C  P  xOz; D = B = C  P  yOz.

Решение любой задачи на уравнения плоскости сводится к одному из двух типов:

. Дана точка на плоскости и вектор , перпендикулярный плоскости.

Искомое уравнение получим, подставляя данные в уравнение (рис. 1):

.

. Дана точка на плоскости и два параллельных плоскости вектора (которые, в частности, могут лежать на плоскости). Берется произвольная точка плоскости М(x, y, z), соединением ее с данной точкой, получается третий вектор. Из компланарности трех векторов следует, что их смешанное произведение равно нулю. Это и будет искомое уравнение плоскости.

В частности, если плоскость проходит через три данные точки , , , не лежащие на одной прямой, то ее уравнение имеет вид:

.

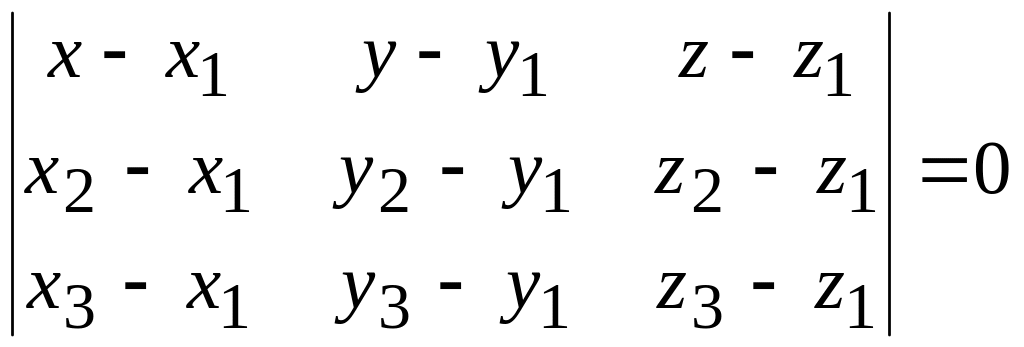Уравнение плоскости в отрезках на осях координат:

,

где a, b, c – отрезки, отсекаемые соответственно на осях Ox, Oy, Oz (рис. 2).

Рис. 2

Расстояние от точки до плоскости  находится по формуле:

.

1. 2. Взаимное расположение плоскостей

Пусть даны две плоскости A₁x+B₁y+C₁z+D₁=0 и A₂x+B₂y+C₂z+D₂=0.

Любые две пересекающиеся плоскости образуют два угла в сумме равные .

Угол  между нормальными векторами плоскостей и равен одному из этих углов и может быть найден по формуле:

.

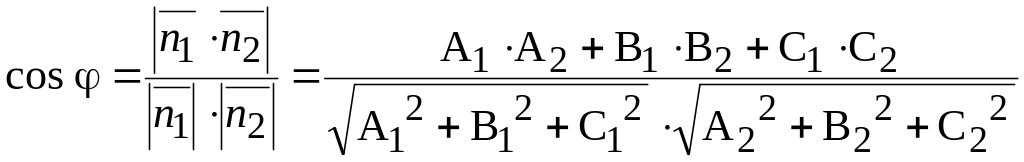Плоскости параллельны, если векторы и коллинеарны, т.е.

.

Плоскости перпендикулярны, если векторы и ортогональны, т.е.

.

Замечание. Если даны три плоскости своими уравнениями A₁x+B₁y+C₁z+D₁=0, A₂x+B₂y+C₂z+D₂=0 и A₃x+B₃y+C₃z+D₃=0, то их общие точки определяются из системы уравнений, составленной из уравнений плоскостей. В случаях, когда нормальные векторы этих плоскостей , , не компланарны, три плоскости имеют единственную общую точку. Тогда их смешанное произведение

и определитель является определителем системы. Такая система имеет единственное решение.