Глава I. Линейное программирование.

1. Примеры задач линейного программирования.

Пример 1. Пусть малое предприятие «Стакан» продает два вида прохладительных напитков, скажем, «Колокольчик» и «Буратино». Оба напитка изготавливаются тут же на месте из имеющихся запасов газированной воды, фруктового сиропа, лимонной кислоты и льда. Нормы расхода сырья на одну порцию готовой продукции и его запасы приведем для удобства в виде таблицы.

Виды сырья	Нормы расхода сырья на 1 порцию продукции		Запасы сырья на одни сутки
	Колокольчик	Буратино
Газированная вода	0,450 л.	0,48 л.	900 л.
Фруктовый сироп	0,050 л.	0,020 л.	80 л.
Лимонная кислота	0,001 л.	0,002 л.	12 л.
Лед в кубиках по 10 г.	20 г.	30 г.	20 кг.

Допустим, что одна проданная порция «Колокольчика» приносит предприятию 5 рублей прибыли, порция «Буратино» - 6 рублей. Также предположим, что нет никаких проблем с изготовлением необходимого количества порций напитков и, что спрос перекрывает предложение.

Возникает вполне естественный вопрос - сколько порций того и другого напитка следует произвести из имеющегося сырья, чтобы получить максимальную прибыль?

Составим математическую модель данной задачи.

Во-первых, введем переменные. Пусть - количество порций «Колокольчика», которое следует произвести, а- количество порций «Буратино».

Во-вторых, введем оптимизируемую целевую функцию, в данном случае прибыль: F.

Тот факт, что следует найти максимум, функции запишем следующим образом:

F(1)

В-третьих, запишем имеющиеся (нетривиальные) ограничения по сырью, вытекающие из того, что объем израсходованного на производство напитков сырья не превышает его суточного запаса.

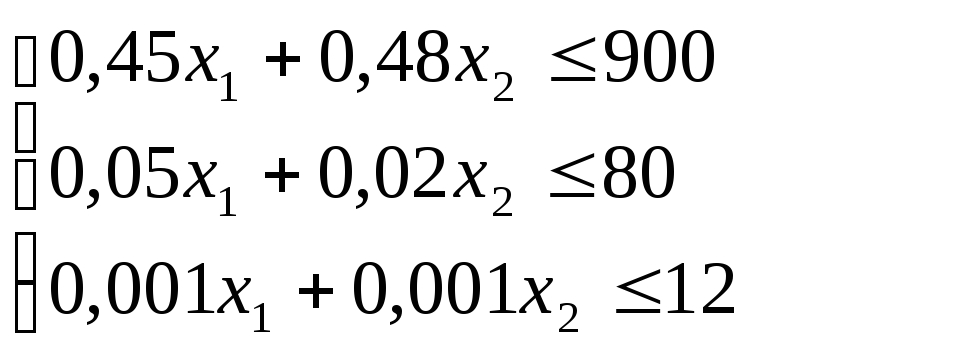(2)

Добавим сюда тривиальные (очевидные) ограничения:

(3)

Условие (1) вместе с ограничениями (2), (3) и дают требуемую математическую модель, которая является частным случаем задачи линейного программирования (см. п. 1.2.).

Как мы увидим позже, модель примера №1 является однородной задачей линейного программирования (см. п. 1.3.).

Дадим обобщение примера №1.

Пример 2. Пусть предприятие выпускает к-типов продукции, используя т-видов ресурсов. При этом расход i-го вида ресурса на единицу j-го вида продукции составляют ; всего имеется объем запасаi-го вида ресурса; реализация единицы продукции j-го вида дает условных денежных единиц прибыли. Требуется составить оптимальный план выпуска продукции.

Модель задачи имеет в этом случае вид:

F

где - объемы планируемого выпуска продукции.

2. Постановка задачи линейного программирования. Основные понятия.

   Определение 1. Задача линейного программирования состоит в оптимизации линейной функции, зависящей от конечного числа вещественных переменных, при заданной системе линейных ограничений (имеющих вид равенства или неравенства).

Определение 2. Зависящая от переменныхфункцияназывается линейной, если она имеет вид:где- некоторые фиксированные вещественные коэффициенты.

Пусть

и

.

Тогда

где

- скалярное произведение векторов в n-мерном арифметическом пространстве . Напомним, чтоn-мерным арифметическим пространством называется множество всех упорядоченных наборовn вещественных чисел () с операциями умножения на числаи сложения, определенными по-координатно:

Элементы пространства ⁿ называются векторами, а само пространство – векторным или линейным.

Определение 3. Ограничения вида:

или

или

называются линейными.

Если положить , то можно записать эти ограничения в векторном виде:

или

или

Другими словами, ограничение, имеющее вид равенства или неравенства, называется линейным, если справа стоит константа, а слева – линейная функция.

Определение 4. Ограничения вида: или

- называются тривиальными.

Эти ограничения записывают обычно в конце системы ограничений задачи линейного программирования (ЛП). Все остальные ограничения называются нетривиальными.

Таким образом, общая задача ЛП может быть представлена в виде:

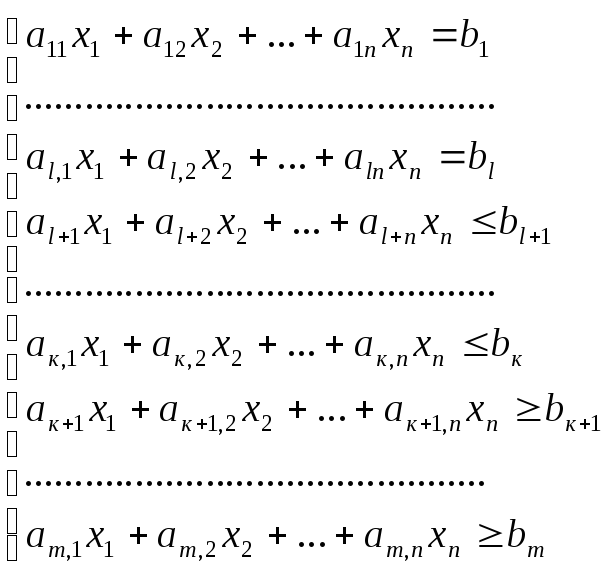(1)

Здесь записьозначает, что следует найтиэкстремум, то есть максимум (max) или минимум (min), функции F.

Определение 5. Оптимизируемая в задаче ЛП функции F называется целевой функцией этой задачи.

Итак, задача ЛП определяется оптимизируемой линейной целевой функцией, нетривиальными линейными ограничениями типа равенства или неравенства и тривиальными ограничениям (которые могут отсутствовать).

Обозначение: Для сокращения записи будем далее писать еслидля всех

В векторном виде задача (1) имеет вид:

(2)

где и- некоторые непересекающиеся подмножества множества индексов

Определение 6. Матрица А=, составленная из коэффициентовсистемы ограничений, называется матрицей системы ограничений, а столбец- столбцом свободных членов.

Заметим, что матрица А имеет размеры mn , то есть состоит из m строк и n столбцов, а вектор состоит из одного столбца. Отметим, что вектор переменныхсостоит из одной строки (или столбца).

Определение 7. Вектор называется возможным решением задачи ЛП, если он удовлетворяет всем нетривиальным ограничениям.

Определение 8. Вектор называется допустимым решением задачи ЛП, если он удовлетворяет всем ограничениям задачи ЛП, включая тривиальные.

Определение 9. Множество всех допустимых решений образует область допустимых решений (ОДР) задачи ЛП.

Определение 10. Вектор коэффициентовпри переменныхцелевой функцииF называется вектором роста целевой функции:

Определение 11. Свободный член целевой функцииназывается начальным значением целевой функции.

Ясно, что

Определение 12. Допустимое решение называется оптимальным, если целевая функцияF достигает на своего экстремума (максимума или минимума) в области допустимых решений.

Смысл названия «вектор роста» становится ясным, если заметить, что вектор является градиентом функцииF, то есть вектором, составленным из частных производных функции F. Действительно, если мы продифференцируем линейную функцию

по переменной , считая остальные переменные постоянными, то конечно получим:

(3)

Как известно из анализа, градиент функции указывает направление максимального роста функции в данной точке. Из (3) видно, что в линейном случае это направление не зависит от точкии совпадает с направлением вектора.

Определение 13. Линией (на плоскости) или поверхностью (в пространстве) уровня функции называется множество точек, удовлетворяющих равенству:

,

где с – некоторая произвольная константа.