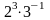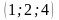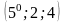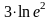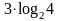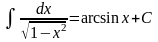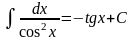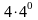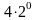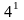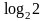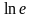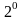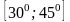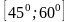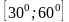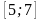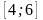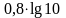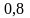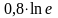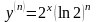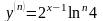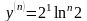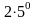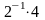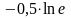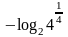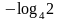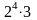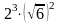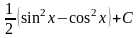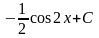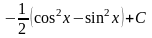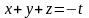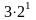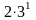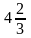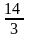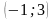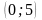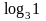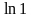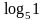Математика
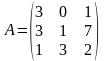 ,
,
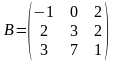 ,
,
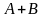 матрицасының мәні:
матрицасының мәні:

. Матрицасының мәні:
Мына өлшемді матрицалардың айырмасын табуға болады:
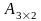 және
және
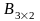
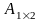 және
және
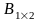
 анықтауышының
мәні:
анықтауышының
мәні:
Анықталған интегралдың негізгі қасиеттері:
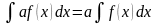 мұндағы
мұндағы
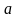 тұрақты
тұрақты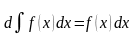

Негізгіинтегралдаркестесініңформуласы:
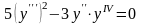 дифференциалдық
теңдеуінің реті неге тең:
дифференциалдық
теңдеуінің реті неге тең:
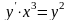 дифференциалдық
теңдеуінің реті:
дифференциалдық
теңдеуінің реті:
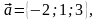
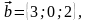
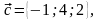 векторларының
аралас көбейтіндісі:
векторларының
аралас көбейтіндісі:
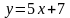 және
және
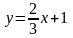 түзулерінің арасындағы бұрыштың
аралығы:
түзулерінің арасындағы бұрыштың
аралығы:
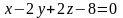 және
және
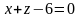 жазықтықтарының
арасындағы бұрыш
жазықтықтарының
арасындағы бұрыш
 -
қа тең
-
қа тең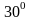 -
тан үлкен
-
тан үлкен
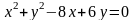 шеңберінің
радиусы жататын аралық:
шеңберінің
радиусы жататын аралық:
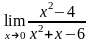 шегінің
мәні:
шегінің
мәні:
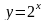 функциясының
функциясының
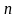 -ші
ретті туындысы:
-ші
ретті туындысы:
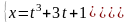 параметрлік
функциясының
параметрлік
функциясының
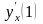 туындысы
туындысы
6-дан кіші
5-ке тең
Егер
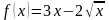 болса,онда
болса,онда
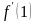 мәні:
мәні:
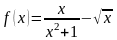 функциясының
функциясының
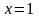 нүктесіндегітуындысы:
нүктесіндегітуындысы:
Сызықтармен шектелген фигураның ауданы:
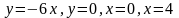
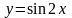 дифференциалдық
теңдеуінің жалпы шешімі:
дифференциалдық
теңдеуінің жалпы шешімі:
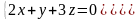 теңдеуінің
шешімі:
теңдеуінің
шешімі:
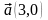 және
және
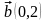 векторлардан құрылған параллелограммның
ауданы:
векторлардан құрылған параллелограммның
ауданы:
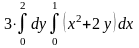 интегралының
мәні:
интегралының
мәні:
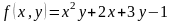 функциясы
үшін
функциясы
үшін
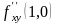 дербес туындысы мына аралықтарда
жатады:
дербес туындысы мына аралықтарда
жатады:
функциясы үшін
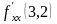 дербес туындысының мәні мына аралықтарда
жатады:
дербес туындысының мәні мына аралықтарда
жатады:
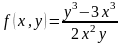 функциясы
біртекті болса, онда оның біртектілік
дәрежесі
функциясы
біртекті болса, онда оның біртектілік
дәрежесі
Келесі матрицалардың қосындысын табуға болады:
А)
 және
және
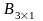
B)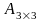 және
және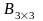
C)
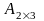 және
және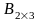
Анықтауышының мәні:
A)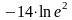
, . Матрицасының мәні:
A)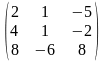
B)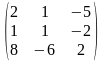
Мына өлшемді матрицалардың айырмасын табуға болады:
A)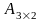 және
және
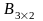
B)
 және
және
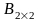
Анықталмаған интегралдың негізгі қасиеттері:
A)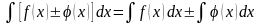
B) мұндағы тұрақты
C)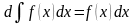
Айнымалылары ажыратылатын дифференциалдық теңдеу:
A)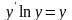
B)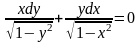
C)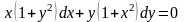
дифференциалдық теңдеуініңреті:
A)
B)
C)
Бірінші ретті дифференциалдық теңдеу:
A)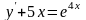
B)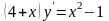
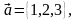
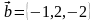 векторларының
скаляр көбейтіндісі:
векторларының
скаляр көбейтіндісі:
A)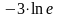
B)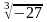
C)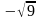
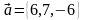 векторларының
ұзындығы:
векторларының
ұзындығы:
A) 11-ге тең
B) 12-ден кіші
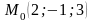 нүктесінен
нүктесінен
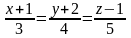 түзуіне
дейінгі арақашықтық:
түзуіне
дейінгі арақашықтық:
A)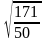
B)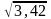
C)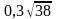
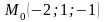 нүктесі
арқылы өтетін
нүктесі
арқылы өтетін
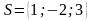 векторына
параллель болатын түзудің параметрлік
теңдеуі:
векторына
параллель болатын түзудің параметрлік
теңдеуі:
A)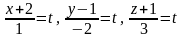
B)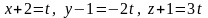
Үлкен жарты осі 5-ке және кіші жарты осі 3-ке тең болатын эллипстің теңдеуі:
A)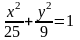
B)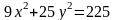
C)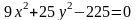
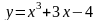 функциясының
туындысының
функциясының
туындысының
 нүктесіндегі
мәні:
нүктесіндегі
мәні:
A)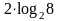
B)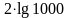
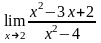 шегінің
мәні:
шегінің
мәні:
A)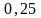
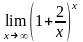 шегі:
шегі:
A) -нен үлкен
-нен үлкен
B)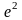 -нен тең
-нен тең
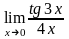 шегінің
мәні:
шегінің
мәні:
A)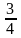
B)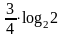
Егер
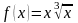 болса,
онда
болса,
онда
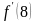 мәні:
мәні:
A)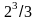
B)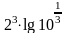
C)