Вопрос 10. Дифференциалы первого и высших порядков и их приложение.

Проведем к графику функции касательную (см. рис.10).

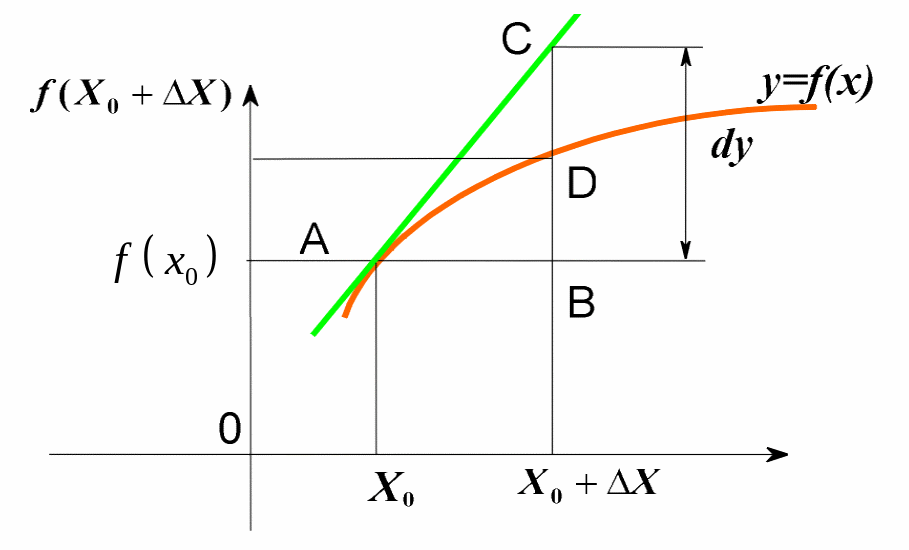
Рисунок 10.

Используем касательную для приближенного вычисления приращения функции .

Касательная имеет уравнение .

Отсюда при находим

.

Символ "" обозначает приближенное равенство при малых .

Выражение в правой части формулы называется дифференциалом функции и обозначается

.

Правила нахождение дифференциалов.

1. d(С)=0 (С –const);

2. dx= , если х – независимая переменная;

3. ;

4. ;

5. d(Cu)=Cdu;

6. , .

Дифференциалом n-го порядка функции f(x) называется дифференциал от дифференциала (n-1)-го порядка этой функции.

.

Формула применяется для приближенного вычисления значений функции.

Вопрос 11. Теоремы о среднем. Правило Лопиталя-Бернулли.

Пусть функция непрерывна в интервале и дифференцируема в интервале . Тогда имеют место теоремы:

1) Теорема Ролля: если , то непременно существует точка , в которой .

2) Теорема Лагранжа: На интервале непременно существует точка , в которой .

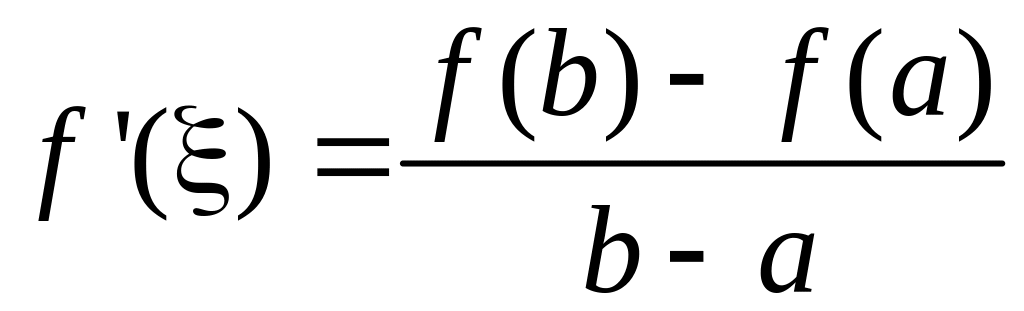3) Теорема о возрастании и убывании функции: Если на интервале , то на этом интервале функция монотонно возрастает; при монотонно убывает.

4) Теорема Коши: Пусть функция непрерывна и монотонна на интервале и дифференцируема на интервале , тогда имеет место формула

где .

Правило Лопиталя-Бернулли.

Пусть . Если функции и дифференцируемы в окрестности точки , и существует конечный или бесконечный предел , то .

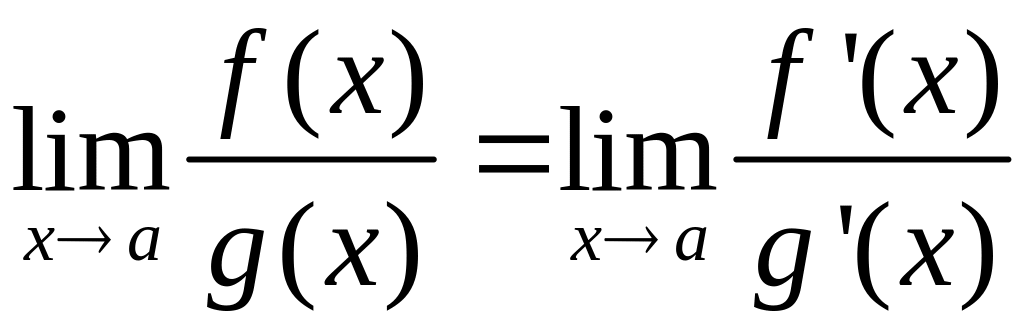Правило Лопиталя-Бернули справедливо также для случая, когда .

Пример 11.

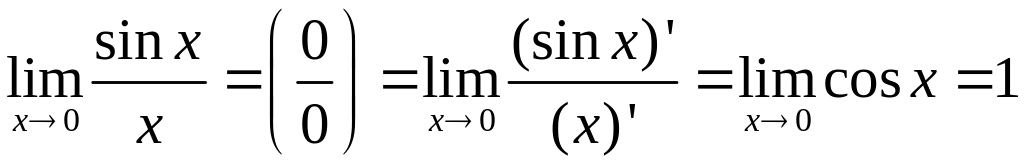
Вопрос 12. Уравнение касательной, уравнение нормали.

Уравнение касательной к кривой y=f(x) имеет вид:

y-y₀=f^/(x₀)(x-x₀).

Уравнение нормали к кривой y=f(x) в точке х₀ имеет вид

Пример 12.

Записать уравнение касательной и нормали к кривой в точке х₀=1.

Вычислив производную в точке х₀=1 получим:

Касательная : y-1=-1(x-1)  y=2-x

Нормаль: y-1=1(x-1)  y=x

Вопрос 13. Наибольшее и наименьшее значение функции на отрезке.

Схема отыскание наибольшего и наименьшего значения функции на отрезке.

1. Найти критические точки. Определить какие из них принадлежат заданному отрезку.

2. Вычислить значение функции в критических точках и на концах отрезка.

3. Выбрать среди найденных значений функции наибольшее и наименьшее.

Пример 13.

Найдем критические точки.

При n=0, х=0, x принадлежит отрезку .

Вычислим значение функции.

.

.

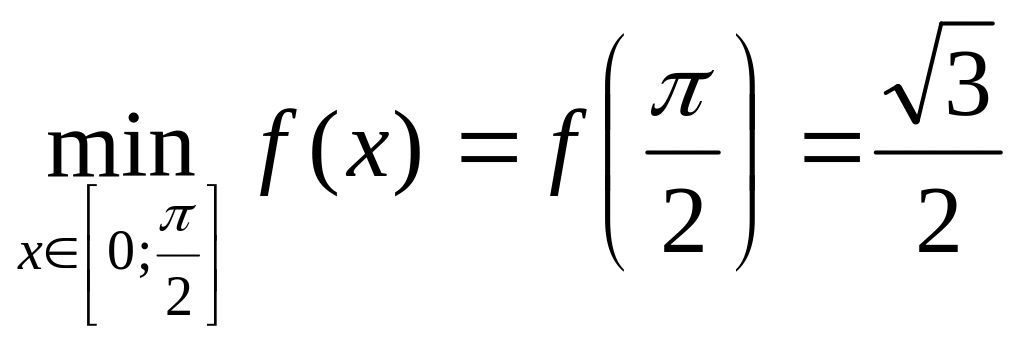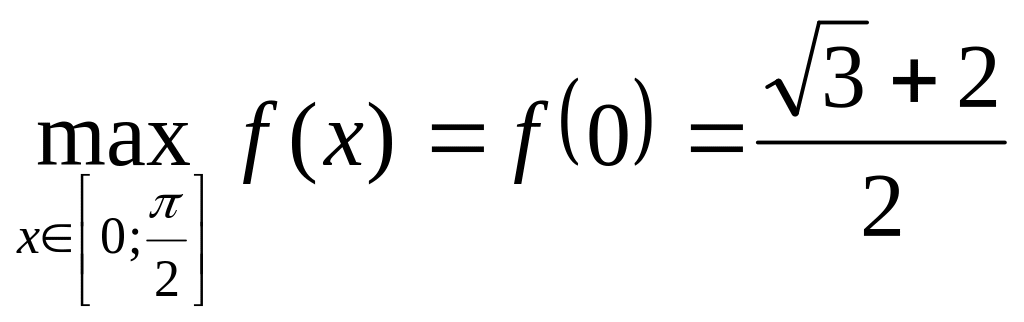Вопрос 14. Приложение производной к исследованию функций и построению графиков. Монотонные функции. Экстремумы.

Функция называется возрастающей на промежутке x, если для любых x₁ и x₂ из этого промежутка таких, что , выполняется неравенство .

Функция называется убывающей на промежутке x, если для любых x₁ и x₂ из этого промежутка таких, что , выполняется неравенство .

Функция, возрастающая в интервале или убывающая в интервале, называется монотонной в этом интервале.

Признаки возрастания функции.

Если дифференцируемая функция y=f(x) в интервале (a,b) возрастает, то её производная в этом интервале неотрицательна, т.е.

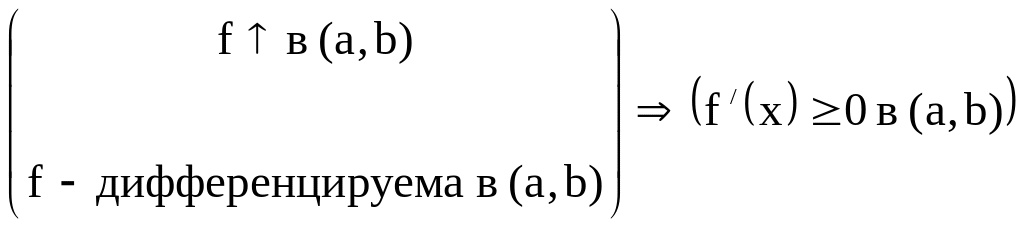
Если непрерывная на отрезке [a,b] и дифференцируемая внутри него функция y=f(x) имеет положительную производную, то f- возрастает на этом отрезке:

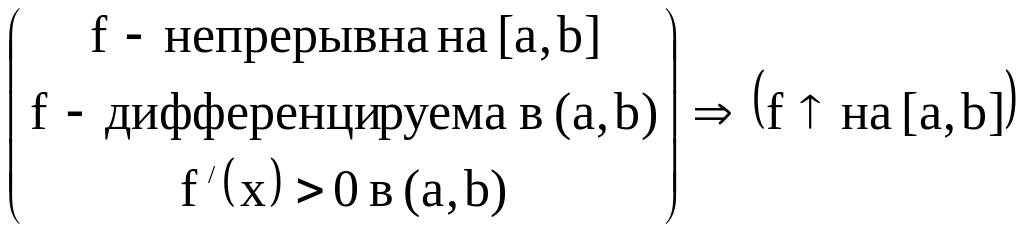
Признаки убывания функция y=f(x) на отрезке [a,b] формулируются аналогично и связываются с отрицательностью производной .

Экстремумом функции называют ее минимальное или максимальное значение.

Определение минимума (максимума): непрерывная функция имеет в точке минимум или максимум, если в достаточно малой окрестности этой точки (слева и справа от нее) все значения функции больше минимального , и все значения функции меньше в случае, когда – точка минимума.

На графике точка экстремума соответствует впадине (минимум) или выступу (максимум). Понятие экстремума относится только к некоторой ограниченной области. Вне ее функция может принимать значения больше максимального или меньше минимального. В связи с этим наряду с экстремумом вводится понятие наибольшего и наименьшего значения функции, как самого большого и самого малого, которые принимает функция на некотором интервале. Наибольшее и наименьшее значение функции выбираются среди ее экстремальных значений и значений на границах интервала.

В точке экстремума касательная к графику функции горизонтальна. Отсюда следует необходимый признак экстремума: если в точке экстремума производная функции существует, то она равна нулю. Однако равенство нулю производной не гарантирует наличие экстремума (необходимый признак не является достаточным). Например, производная функции при обращается в нуль, но экстремума в этой точке нет.

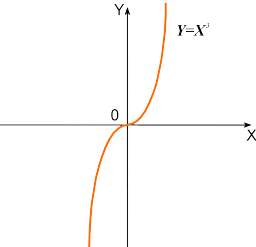
Рисунок 11.

Полностью вопрос об экстремумах решается с помощью необходимого и достаточного признака существования экстремума: функция имеет в точке экстремум, если производная меняет знак при переходе через эту точку; экстремум является минимумом при изменении знака производной с (-) на (+) и максимумом при изменении знака с (+) на (-).

Пример 14.

1. Исследовать на экстремум функцию

Дифференцируем функцию и отыскиваем нули ее производной

,

,

,

,

.

Исследуем знак производной:

на интервале будет ,

-

-

Отсюда при функция имеет максимум ; при - минимум .

Задачи на отыскание наименьших и наибольших значений.

Рассмотренный метод отыскания экстремальных значений функции широко применяется при решении прикладных задач, в которых требуется отыскать наибольшее или наименьшее значение какого-нибудь параметра.