Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Ульяновский государственный технический университет

Процедура ортогонализации Грамма-Шмидта и разложение сигнала по ортонормальным системам функций

Методические указания к выполнению лабораторных работ по курсу «Введение в теорию сигналов» для студентов направления 230401,квалификации 23040165 «Инженер-математик»

Ульяновск 2009

СОДЕРЖАНИЕ

2. Краткие теоретические сведения 3

3. Задание на лабораторную работу 19

4. Содержание отчета 20

5. Список контрольных вопросов 21

1. Цель работы

Основной целью лабораторной работы является изучение способов ортогонализации и ортонормированных систем функций, аппроксимация заданного сигнала с помощью ортонормированных функций и изучение влияния количества членов ряда на качество аппроксимации сигнала.

2. Краткие теоретические сведения

При распространении положений векторного базисного пространства на функциональное пространство , в качестве координатного базиса пространства мы должны использовать совокупность функций , в пределе - бесконечную, которая должна быть системой ортогональных функций , т.е. все функции на этом отрезке должны быть взаимно ортогональны:

Система ортогональных функций на интервале будет ортонормальной, если все функции системы при имеют единичную норму, т.е. выполняются условия:

.

Эти условия можно записать в следующей обобщенной форме:

.

Система ортогональных функций всегда может быть превращена в ортонормальную путем нормировки, т.е. деления всех функций на их норму.

Разложение сигнала в ряд

Произвольный сигнал (пространство Гильберта), заданный на интервале , может быть разложен в ряд по упорядоченной системе ортонормированных базисных функций 

. (1)

Для нахождения значений коэффициентов умножим обе части данного выражения на базисную функцию с произвольным номером и проинтегрируем результаты по переменной , при этом получим

.

С учетом ортонормальности функций , в правой части этого равенства остается только один член суммы с номером при , который, по левой части уравнения, представляет собой скалярное произведение сигнала и соответствующего базисного вектора, т.е. проекцию сигнала на соответствующее базисное направление

. (2)

Таким образом, в геометрической интерпретации коэффициенты представляют собой проекции вектор - сигнала на соответствующие базисные направления , т.е. координаты вектора по координатному базису, образованному системой ортогональных функций , в пределе - бесконечномерной. При практическом использовании количество членов ряда (1) ограничивается определенным значением , при этом для любого значения совокупность коэффициентов обеспечивают наименьшее по средней квадратической погрешности приближение к заданному сигналу.

Используя понятия, введенные ранее, рассмотрим теперь задачу сопоставления произвольному сигналу с ограниченной энергией, т.е. временной функции (возможно, комплексной) ее численного представления. Задача сводится к нахождению подходящего отображения пространства в пространство , причем обычно выбирается компромиссно, с учетом точности и экономичности представления. Поскольку число измерений пространства бесконечно, а конечно, отображение должно быть типа «много в одно»; это подразумевает такую степень приближения, при которой произвольный сигнал из не может иметь представления в , отличного от представления всех других сигналов. К таким изображениям естественно подходить с позиций отношения эквивалентности. Мы разбиваем пространство на множества эквивалентности, каждому из которых взаимнооднозначно соответствует некоторая точка в .

Обычный подход к этой задаче состоит в выборе некоторого - мерного подпространства из . Пусть есть система линейно независимых функций в , так что при условие

выполняется почти всюду в том и только в том случае, если при всех .

Обозначим через линейное подпространство, натянутое на эти функции. Если рассматриваемый сигнал принадлежит , то он может быть единственным образом представлен в виде линейной комбинации :

и набор чисел (вектор - строка) образует искомое представление в . Поскольку есть пространство со скалярным произведением

,

то отношение между и может быть выражено в матричной форме:

или

,

где .

Применяя другую запись, введем в взаимные базисные функции , которые могут быть представлены в виде линейной комбинации ;

,

причем

,

или в матричной форме

.

Используя взаимный базис, можно теперь написать

.

При определении базисных функций для представления сигнала часто используют понятие нормы с весом, для того, чтобы обратить особое внимание на некоторый участок области определения функции.

– удовлетворяет условиям скалярного произведения, где - вещественная неотрицательная функция, определенная на интервале . А система функций – ортонормальна с весом , если

.

При этом базисные функции претерпевают небольшие изменения:

,

где – ортонормальны в обычном смысле, а – с весом .

Возможность разложения непрерывных сигналов и функций в обобщенные ряды по системам ортогональных функций имеет огромное принципиальное значение, так как позволяет вместо изучения несчетного множества точек сигнала ограничиться счетной системой коэффициентов ряда.

К системам базисных функций, которые используются при разложении сигналов, предъявляют следующие основные требования:

-для любого сигнала ряд разложения должен сходиться;

-при ограничении ряда по уровню остаточной погрешности расхождения с заданным сигналом количество членов ряда должно быть минимальным;

-базисные функции должны иметь достаточно простую аналитическую форму;

-коэффициенты разложения в ряд должны вычисляться относительно просто.

Процедура ортогонализации Грамма-Шмидта

Важное значение имеет построение ортогональных базисов. Одним из наиболее употребляемых способов при этом является так называемый рекуррентный способ ортогонализации Грама-Шмидта, который заключается в следующем.

Пусть в задана система линейно независимых векторов. Тогда система ортонормальных векторов получается путем нормализации вспомогательных векторов по следующему правилу:

, ,

, ,

, ,

. . . . . . .

, .

Заметим, что если функции переставить местами, то получим другую, но тоже ортонормальную систему.

Рассмотрим пример. Применим процедуру Грамма-Шмидта к последовательности функций , определенных на отрезке . В этом случае .

, , ,

, , ,

,

,

. . . . . . .

Разложение сигнала по ортонормальным системам функций

Согласно теореме Дирехле, любой сигнал , имеющий конечное число точек нарушения непрерывности первого рода, и конечный по энергии на интервале , может быть разложен по системе ортонормальных функций, если существуют интегралы модуля сигнала и модуля его первой производной, т.е.:

.

Ортонормированные системы функций хорошо известны в математике. Выбор типа функций в качестве координатного базиса сигнального пространства, определяется удобством и простотой последующего использования при математической обработке сигналов.

Рассмотрим примеры наиболее употребляемых ортонормированных систем функций, используемых для представления сигналов с заданными областью определения и весовой функцией .

1. Комплексные гармонические функции

Для комплексных гармонических функций и , функции уже ортогональны, следовательно, для получения ортонормальной системы их нужно нормировать, то есть поделить на норму соответствующей функции ряда. Найдем эту норму

.

Разложение

,

где

это представление рядом Фурье функций, которые ограниченных на отрезке , а также периодических с периодом, равным . Однако, это представление применимо для функций, заданных на любом конечном интервале, который можно привести к интервалу выбором подходящего масштаба по оси времени.

Рассмотрим пример. Пусть требуется с помощью гармонических функций представить сигнал, приведенный на рис. 1.(в дальнейшем будем рассматривать заданный сигнал).

Рис. 1.

Задан трапецевидный сигнал на интервале (рис. 1):

Необходимо представить его рядом комплексных гармонических функций, то есть в виде

.

К омплексные гармонические функции определены на интервале , следовательно, и исходный сигнал должен быть задан на этом же интервале. Для этого подвергнем его сжатию в раза, а затем произведем сдвиг на влево. Новый сигнал будет описываться формулой (рис. 2).

Рис. 2.

Коэффициенты разложения найдем по формуле

.

Затем переходим к исходному масштабу и получаем аппроксимированный исходный сигнал. Графики для различных приведены на рис. 3.

Рис. 3.

Найдем квадратическое отклонение исходного сигнала от его приближения:

для ;

для .

Найдем максимальную ошибку приближения: . Для этого построим графики функции для и (рис.4).

Рис. 4.

Из графиков видно, что:

для и достигается при ;

для и достигается при .

2. Полиномы Лежандра

Для и можно получить другую ортонормальную систему, применив процедуру Грамма-Шмидта к последовательности . В результате получаются нормированные полиномы:

где - полиномы Лежандра. Эти полиномы можно также считать по формуле

или по рекуррентной формуле

.

Полином имеет нулей, все они вещественны и находятся в интервале .

Разложим рассмотренный выше сигнал. Коэффициенты разложения найдем по формуле

.

Аппроксимированный сигнал представлен на рис. 5.

Рис. 5.

3. Полиномы Чебышева

Для и полиномы , образуют ортонормальную систему, где - полиномы Чебышева, заданные следующим образом:

Для удовлетворяют рекуррентной формуле

.

Свойство полиномов Чебышева: из всех полиномов -ой степени, имеющих коэффициент при , равный 1, на интервале наименее отклоняются от нуля.

Без весовой функции (рис. 6)

.

Рис. 6.

С весовой функции (рис. 7)

.

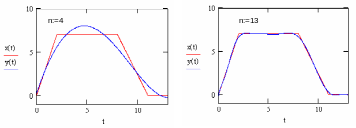
Рис. 7.

4. Функции Лагерра

Для и полиномы

образуют ортонормальную систему. Здесь - полиномы Лагерра, задаваемые формулой

.

Они имеют вещественных нулей на и удовлетворяют рекуррентному соотношению

.

Функции Лагерра имеют единичный вес и ортонормальны на

.

Разложим рассматриваемый нами сигнал. Коэффициенты разложения найдем по формуле

.

Аппроксимированный сигнал представлен на рис. 8.

Рис. 8.

Они также могут быть получены применением процедуры Грамма-Шмидта к последовательности . Функции Лагерра могут быть реализованы практически как импульсные реакции сравнительно простых физических цепей конечного порядка. Для этого их записывают как

.

Функции имеют преобразование Лапласа вида

,

откуда видно, что -ая функция Лагерра - это импульсная реакция цепи, один каскад которой имеет передаточную функцию , а последующих одинаковы с функцией , т. е. это фазовращатели, не изменяющик энергию сигнала. Это так называемый «трансверсальный» фильтр, импульсная реакция которого есть произвольная линейная комбинация функций Лaгерра.

5. Функции Лежандра

Подстановка преобразует интервал для величины в интервал для величины , поэтому из полиномов Лежандра можно получить еще одну систему функций, ортонормальных на ( - произвольный действительный положительный параметр). Функции Лежандра

образуют ортонормальную систему на с единичным весом. Преобразования Лапласа от этих функций имеют полюсы при

Графики аппроксимированного исходного сигнала для различных приведены на рис. 9. При этом параметр подбирается произвольно в зависимости от исходного сигнала.

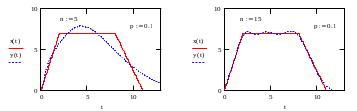
Рис. 9.

6. Функции Чебышева

Преобразованием Чебышева получаем функции

,

которые ортонормальны с весом на . Полюсы преобразования Лапласа получаются при

Графики аппроксимированного исходного сигнала для различных приведены на рис. 10

Рис. 10.

7. Функции Эрмита

Для и полиномы

образуют ортонормальную систему. - полиномы Эрмита, которые задаются в виде

или рекуррентной формулой

.

Функций Эрмита

ортонормальны с единичным весом на и могут быть получены процедурой Грама-Шмидта к последовательности .

Разложим рассматриваемый нами сигнал. Исходный сигнал можно предварительно задать на интервале (рис. 11).

Рис. 11.

Коэффициенты разложения найдем по формуле

.

Аппроксимированный сигнал представлен на рис. 12.

Рис. 12.

8. Функции Уолша

Для и можно построить полную ортонормальную систему функций типа «прямоугольных волн». Каждая -ая функция содержит прямоугольных волн, поэтому в обозначении функции удобно использовать два индекса:

Эта система важна для практики, поскольку функции кусочно-постоянны и принимают лишь два значения ( или ). Подобные сигналы могут быть легко получены с помощью двоичных логических схем. Перемножение таких сигналов для получения, скажем, скалярного произведения производится очень просто, с помощью ключа, изменяющего полярность и включаемого в нужные моменты времени. Заметим, что функции соответствуют обычным прямоугольным волнам. Мы можем перейти к соответствующей одноиндексной системе, упорядочив функции так, чтобы -ая функция раз пересекала нулевой уровень на интервале (т.е. раз меняла знак). Это достигается при следующих обозначениях:

,

где (рис. 13).

Рис. 13.

Функции Уолша определены на интервале , следовательно, и исходный сигнал должен быть задан на этом же интервале. Для этого подвергнем его сжатию в . Новый сигнал будет описываться формулой (рис. 14).

Рис. 14.

Коэффициенты разложения найдем по формуле

.

.

Графики для различных приведены на рис. 15.

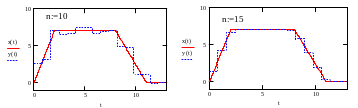
Рис. 15.