9.3. Напряженное состояние. Условия прочности
При чистом изгибе волокна сечения, удаленные от нейтрально линии, испытывают либо напряжения растяжения, либо напряжения сжатия. Соответственно, напряженное состояние в этих волокнах будет таким же, как при простом растяжении – сжатии, т.е. линейным, но в отличие от простого растяжения, неоднородным (напряжения изменяются по мере удаления от нейтральной линии).
Для материалов, одинаково сопротивляющихся растяжению и сжатию, при проверке прочности самое большое по абсолютной величине напряжение сравнивают с допускаемым, т.е. условия прочности имеют вид
.
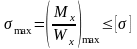(9.23)
Если сопротивление материала растяжению и сжатию различно, то следует отдельно проверить условия прочности для растянутых и сжатых волокон:
- при растяжении
,
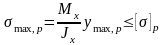- при сжатии
,
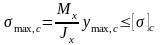(9.24)
где ymax,p и ymax,c – расстояние от оси Ox до наиболее удаленных волокон, находящихся в зонах растяжения и сжатия, соответственно.
9.4. Потенциальная энергия деформации при чистом изгибе
Рассмотрим элемент балки длиной dz (рис. 9.9). Считая левое сечение неподвижным, определим работу, совершаемую изгибающим моментом Mx, который приложен к правому сечению.
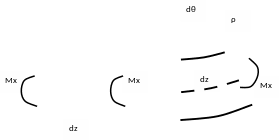
Рис. 9.9. Потенциальная энергия при изгибе
Предполагаем, что работа полностью переходит в потенциальную энергию деформации. Тогда,
.
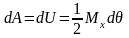(9.25)
Длина
нейтральной линии, как следует из рис.
9.9, будет равна
.
Учитывая выражение (9.17), получим
.
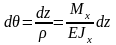(9.26)
Подставляем (9.26) в (9.25) и получаем потенциальную энергию, накопленную элементом балки длиной dz:
.
(9.27)
Потенциальная энергия, накопленная балкой длиной l, равна
.
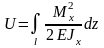(9.28)
9.5. Определение прогибов. Дифференциальное уравнение упругой линии балки
Рассмотрим деформацию балки при прямом изгибе. Ось балки в данном случае искривляется в главной плоскости, совпадающей с силовой плоскостью, а поперечные сечения поворачиваются без искажения. Перемещение центра тяжести сечения балки в направлении, перпендикулярном ее продольной оси, называется прогибом. Угол, на который поворачивается данное сечение по отношению к своему исходному положению, называется углом поворота сечения.
Изобразим ось балки или, как принято называть, ее упругую линию в деформированном состоянии (рис. 9.10).
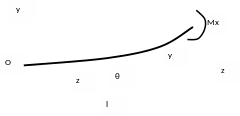
Рис. 9.10. Упругая линия балки
Выбираем систему координат Oyz . Прогиб сечения, удаленного от начала координат на расстояние z, обозначим y, а угол поворота данного сечения, равный углу между касательной к упругой линии в данной точке и осью Oz, обозначим θ. Тогда кривизна упругой линии балки постоянного поперечного сечения в рассматриваемой точке в соответствии с формулой (9.17) будет равна
.
Для кривизны плоской кривой в курсе высшей математике получена формула
.
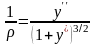(9.29)
Приравнивая (9.17) и (9.29), получим
.
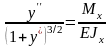(9.30)
Выражение (9.30) представляет собой нелинейное дифференциальной уравнение второго порядка. Опыт расчета прогибов авиационных конструкций при оценке их жесткости показывает, что квадратом первой производной от прогиба y'2 можно пренебречь по сравнению с единицей, тогда получим приближенное дифференциальное уравнение упругой линии балки
.
(9.31)
При решении уравнения (9.31) постоянные интегрирования определяются из граничных условий. Если балка имеет несколько характерных участков, отличающихся аналитическими выражениями для изгибающих моментов, то решение уравнения для каждого участка после интегрирования содержит две постоянные. При n участках таких постоянных, требующих определения – 2n. В сопротивлении материалов предложены ряд графических и аналитических приемов, позволяющих уменьшить число постоянных интегрирования. Однако в настоящее время такие решения потеряли свою актуальность в связи с широким использованием численных методов интегрирования, которые позволяют вычислить выражение для упругой линии балки с высокой точностью. Вместе с тем, аналитическое выражение упругой линии балки при изгибе применяется при решении ряда динамических задач сопротивления материалов и в теории колебаний.