Алгоритм решения дробно – рациональных уравнений

1. Перенести все члены уравнения в одну часть.

2. Преобразовать эту часть уравнения к виду

алгебраической дроби = 0. .

3.Перейти к системе h ( x ) = 0

q ( x ) ≠ 0

4. Решить уравнение h ( x ) = 0.

5. Сделать проверку q ( x ) ≠ 0.

6. Записать ответ.

Пример. + = 2

+ - 2 = 0

= 0

= 0

= 0

= 0

= 0

2x (8 - x) = 0

(x - 2) (x + 2) ≠ 0

2 x = 0, 8 - x = 0

х = 0, х = 8

Проверка: (0 - 2) (0 + 2) ≠ 0 (и)

(8 - 2) (8 + 2) ≠ 0 (и)

Ответ: 0;8.

Графический способ в решении систем уравнений

1. Выражаю у через х в каждом из уравнений.

2. Строю графики уравнений:

• По алгоритму построения параболы.

• С помощью таблицы.

• С помощью производной.

1. З аписываю координаты точек пересечения в ответ.

П ример. х = - 1 у

х ² + у = 4

х = - 1

у = - х ² + 4 0 1

х

Ответ: (- 1; - ); (- 1; ).

Алгоритм решения иррационального уравнения

1. Уединяю корень 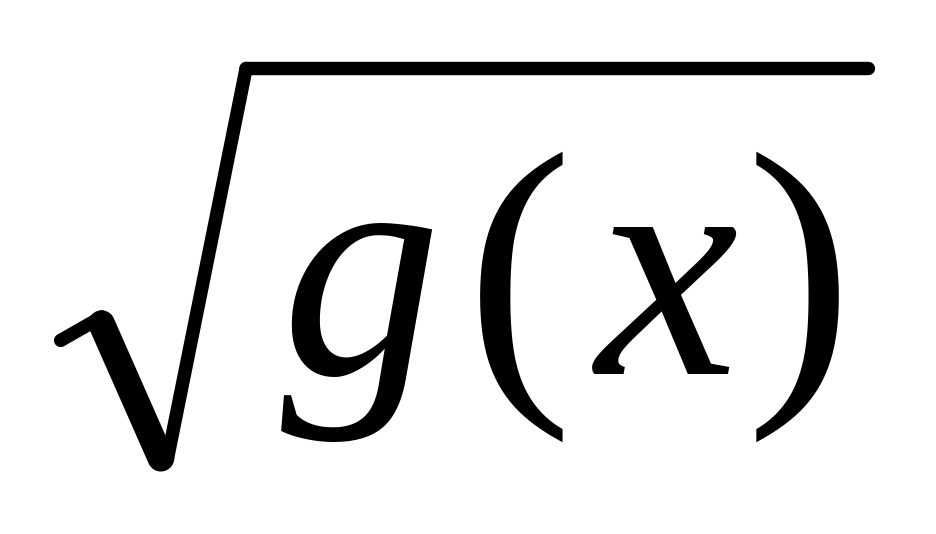= f (x)

2. П ерехожу к системе: g (x) = f ² (x)

f (x) ≥ 0

3. Решаю получившееся уравнение.

4. Делаю проверку.

5. Пишу ответ.

Пример. 2 х + - 3 = 0

= 3 – 2 х

х = ( 3 – 2 х ) ²

3 – 2 х ≥ 0

х = 9 – 12 х + 4 х ²

4 х ² – 13 х + 9 = 0

х ₁ = , 3 – 2* ≥ 0 ( и )

х ₂ = 3 , 3 – 2*3 ≥ 0 ( л )

Ответ: .

Пример. Замена уравнения системой.

Пример. Использование сопряженного выражения.

Пример. Возведение в квадрат или в куб.

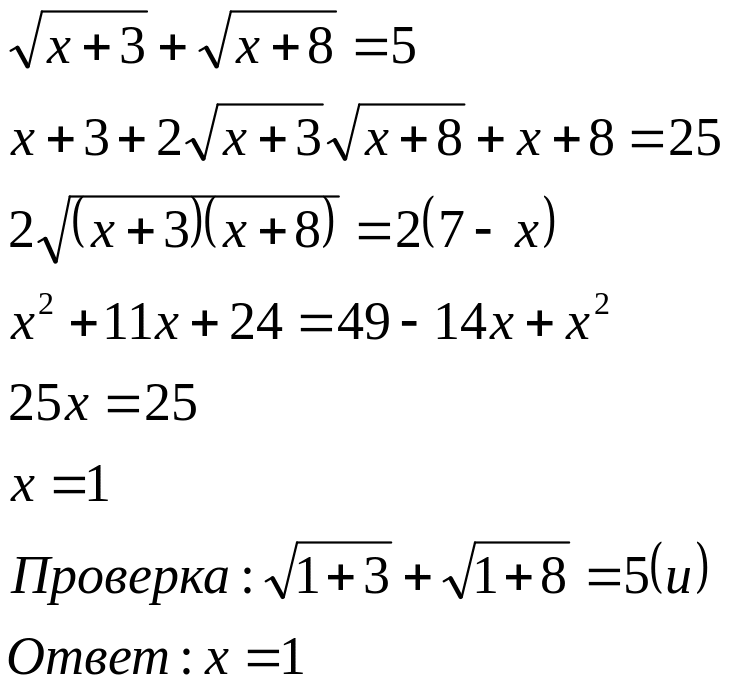
Иррациональные неравенства

1 случай

1 +х ≥0

х + 3 ≥ (1+ х)²

х ≥ - 1

х² +х -2 ≥0

2 случай

1 + х < 0

х + 3 ≥

х < -1

х ≥ -3

Ответ:

[1;+∞) U [-3;- 1)

Методы решения показательных уравнений

• a ^{f (x)} = a ^{g (x)} f (x) = g (x), а > 0, а ≠ 1

• Привожу обе части уравнения к одному основанию, используя свойства степеней.

• Приравниваю показатели.

• Решаю получившееся линейное уравнение.

• Пишу ответ.

П ример.

Ответ: -2

• Вынесение общего множителя за скобку

Ответ: 3

• Графический

• Введение новой переменной:

• a t ^{2 x} + b t ^x + c = 0 , t ^x = у

2^2х -6*2^х +8=0

(2^х)²-6*2^х+8=0

2^х =у

у²-6у +8=0

у₁=2 у₂=4

2^х=2 2^х=4

х=1 2^х=2²

х=2

Ответ:1,2

• a t ^{2 x} + b t ^x z ^x + c z ^2x = 0 : z ^x - однородное уравнение 2 степени

:2^2х

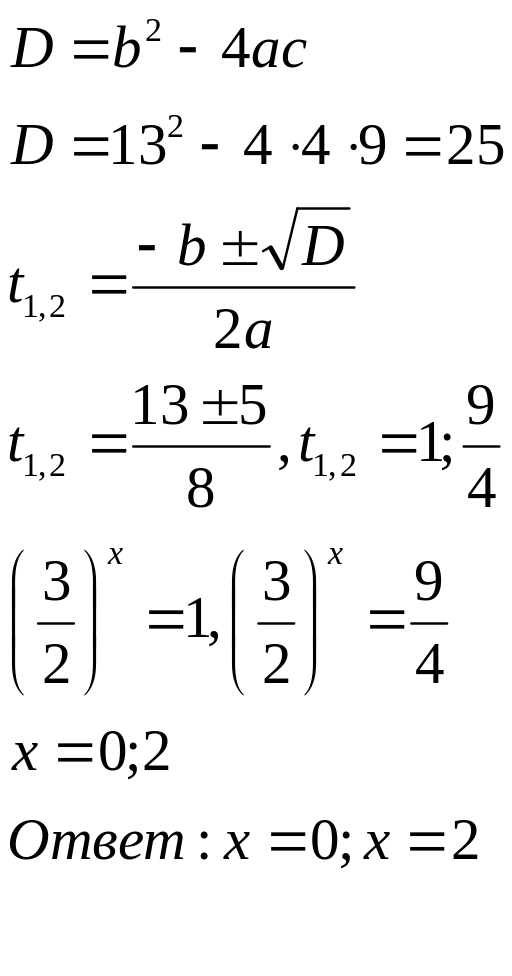
• 5 ^x = 8 ^x - однородное уравнение 1 степени

5 ^х = 8 ^х |:8^x

• Степенно- показательные уравнения

(х - 3)^{3х2 – 10х +3} = 1

1) х – 3 = 1, откуда х = 4, так как любая степень 1 равна 1

2) х – 3 = - 1, то есть х = 2, в этом случае показатель должен

быть четным

х – 3 = - 1

3х² – 10х + 3 = 2n, n є N, но

при х = 2 выражение 3х² – 10х + 3 ≠ 2n, решений нет

3) 3х² – 10х + 3 = 0

х – 3 ≠ 0, так как 0⁰ не имеет смысла

х = 1/3

Ответ. х₁ = 1/3, х₂ = 4